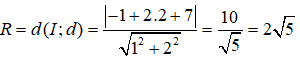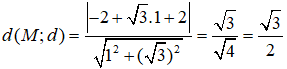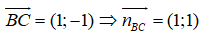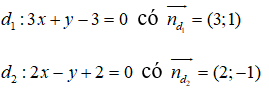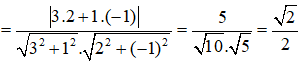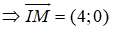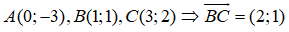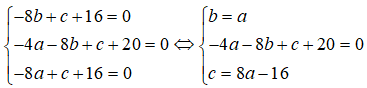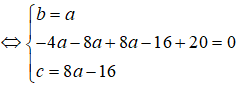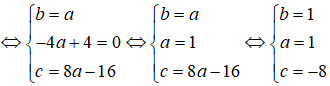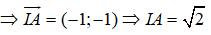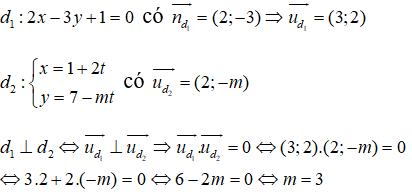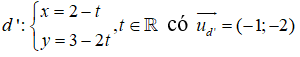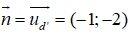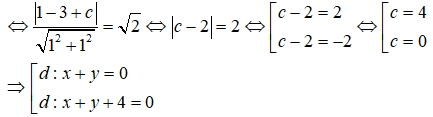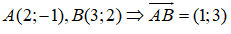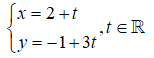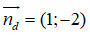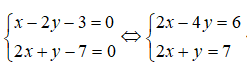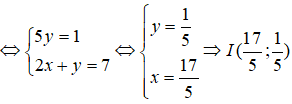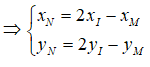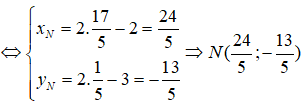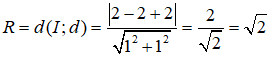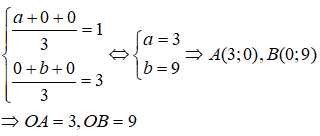23 câu hỏi trắc nghiệm thuộc Đề kiểm tra 45 phút Hình học 10 Chương 3 có đáp án (Đề 3)

Câu 1:

Phần I: Trắc nghiệm

Khẳng định nào dưới đây là đúng nhất về các vecto chỉ phương $\vec{u_{1}} v à \vec{u_{2}}$ của d?

A. $\vec{u_{1}} = k \vec{u_{2}}, (k \neq 0)$

B. $\vec{u_{1}} = \vec{u_{2}}$

C. $\vec{u_{1}} + \vec{u_{2}} = 0$

D. $\vec{u_{1}} . \vec{u_{2}} = 0$

Xem đáp án

Đáp án: A

Câu 2:

Bán kính đường tròn (C) có tâm I(-1;2) và tiếp xúc với đường thẳng d: x + 2y + 7 = 0 bằng:

A. $R = \sqrt{5}$

B. $R = 2 \sqrt{5}$

C. $R = \frac{1}{\sqrt{5}}$

D. $R = 2$

Xem đáp án

Đáp án: B

Vì (C) tiếp xúc với đường thẳng d nên:

Câu 3:

Phương trình tổng quát của đường thẳng d đi qua điểm M(2;-3) và nhận vecto $\vec{n} = (3; - 2)$ làm vecto pháp tuyến là?

A. 2x - 3y - 12 = 0

B. -2x + 3y - 12 = 0

C. 3x - 2y - 12 = 0

D. -3x + 2y - 12 = 0

Xem đáp án

Đáp án: C

Phương trình tổng quát của đường thẳng d đi qua M(2;-3) và nhận $\vec{n} = (3; - 2)$ làm vecto pháp tuyến có dạng:

3(x - 2) - 2(y + 3) = 0 ⇔ 3x - 2y - 12 = 0

Câu 4:

Cho đường thẳng $d : \{\begin{cases} x = 1 - 2 t \\ y = 6 t \end{cases}$ . Điểm nào dưới đây nằm trên đường thẳng d?

A. M(1;6)

B. N(-2;6)

C. P(1;-2)

D. Q(1;0)

Xem đáp án

Đáp án: D

Lần lượt thay tọa độ các điểm vào đường thẳng ta thấy điểm Q ở đáp án D thỏa mãn phương trình đường thẳng ứng với giá trị t = 0. Do đó, Q thuộc d

Câu 5:

Phương trình của đường tròn (C) biết tâm I(2;7) và bán kính bằng 4 là:

A. (x + 2 $)^{2}$ + (y + 7 $)^{2}$ = 4

B. (x - 2 $)^{2}$ + (y - 7 $)^{2}$ = 4

C. (x + 2 $)^{2}$ + (y + 7 $)^{2}$ = 16

D. (x - 2 $)^{2}$ + (y - 7 $)^{2}$ = 16

Xem đáp án

Đáp án: D

Phương trình của đường tròn (C) biết tâm I(2;7) và bán kính bằng 4 có dạng:

(x - 2 $)^{2}$ + (y - 7 $)^{2}$ = $4^{2}$ ⇔ (x - 2 $)^{2}$ + (y - 7 $)^{2}$ = 16

Câu 6:

Khoảng cách từ điểm M(-2;1) tới đường thẳng d: x + $\sqrt{3}$ y + 2 = 0 bằng:

A. $\frac{4 \sqrt{3}}{3}$

B. $\frac{1}{2}$

C. 2

D. $\frac{\sqrt{3}}{2}$

Xem đáp án

Đáp án: D

Khoảng cách từ điểm M(-2;1) tới đường thẳng d: x + $\sqrt{3}$ y + 2 = 0 bằng:

Câu 7:

Cho tam giác ABC có các đỉnh A(-1;3), B(1;0) và C(2;-1). Tính độ dài đường cao của tam giác ABC vẽ từ điểm A?

A. 1

B. $\frac{\sqrt{2}}{2}$

C. $\sqrt{2}$

D. $\frac{3 \sqrt{2}}{2}$

Xem đáp án

Đáp án: B

Ta có A(-1;3), B(1;0) và C(2;-1)

Phương trình đường thẳng BC có dạng: (x - 1) + (y - 0) = 0 ⇔ x + y - 1 = 0

Độ dài đường cao của tam giác ABC kẻ từ điểm C chính bằng khoảng cách từ điểm A đến đường thẳng BC:

Câu 8:

Với giá trị nào của tham số m thì phương trình $x^{2}$ + $y^{2}$ - 4x + 2y - m + 1 = 0 là phương trình của một đường tròn?

A. m ≥ -4

B. m ≤ -4

C. m > -4

D. m < -4

Xem đáp án

Đáp án: C

$x^{2}$ + $y^{2}$ - 4x + 2y - m + 1 = 0 ⇔ (x - 2 $)^{2}$ + (y + 1 $)^{2}$ = m + 4 (*)

Để (*) là phương trình của một đường tròn thì: m + 4 > 0 ⇔ m > -4

Câu 9:

Đường tròn (C): $x^{2}$ + $y^{2}$ + 6x - 8y - 11 = 0 có tâm I và bán kính bằng bao nhiêu?

A. I(3;-4), R = 36

B. I(-3;4), R = 36

C. I(3;-4), R = 6

D. I(-3;4), R = 6

Xem đáp án

Đáp án: D

(C): $x^{2}$ + $y^{2}$ + 6x - 8y - 11 = 0 ⇔ (x + 3 $)^{2}$ + (y - 4 $)^{2}$ = 11 + 25

⇔ (x + 3 $)^{2}$ + (y - 4 $)^{2}$ = 36 ⇔ (x + 3 $)^{2}$ + (y - 4 $)^{2}$ = $6^{2}$

Vậy đường tròn (C) có tâm I(-3;4) và bán kính R = 6

Câu 10:

Góc giữa hai đường thẳng d1: 3x + y - 3 = 0 và d2: 2x - y + 2 = 0 bằng bao nhiêu?

A. 30 $°$

B. 45 $°$

C. 60 $°$

D. 90 $°$

Xem đáp án

Đáp án: B

Gọi góc giữa hai đường thẳng là α

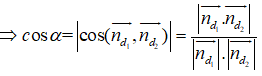
⇒ α = 45 $°$

Câu 11:

Phương trình tiếp tuyến của đường tròn (C): $x^{2}$ + $y^{2}$ + 4x - 6y - 3 = 0 tại điểm M(2;3) là:

A. x - 2 = 0

B. y - 3 = 0

C. 2x - 3y + 5 = 0

D. -2x + 3y - 5 = 0

Xem đáp án

Đáp án: A

(C): $x^{2}$ + $y^{2}$ + 4x - 6y - 3 = 0 ⇔ (x + 2 $)^{2}$ + (y - 3 $)^{2}$ = 16

Đường tròn (C) có tâm I(-2;3)

Gọi d là phương trình tiếp tuyến của (C) tại M. Suy ra, d đi qua M và nhận IM là vecto pháp tuyến

⇒ d: 4(x - 2) + 0.(y - 3) = 0 ⇔ x - 2 = 0

Câu 12:

Cho đường thẳng d có phương trình $d : \{\begin{cases} x = 2 - 7 t \\ y = 1 + 6 t \end{cases}, t \in ℝ$ . Khi đó, một vecto chỉ phương của d là:

A. $\vec{u} = (2; - 7)$

B. $\vec{u} = (1; 6)$

C. $\vec{u} = (2; 1)$

D. $\vec{u} = (- 7; 6)$

Xem đáp án

Đáp án: D

Câu 13:

Cho tam giác ABC có các đỉnh A(0;-3), B(1;1), C(3;2). Khi đó, đường cao của tam giác vẽ từ đỉnh A có phương trình:

A. 2x - y - 2 = 0

B. x - 2y - 6 = 0

C. 2x + y + 3 = 0

D. x + 2y - 8 = 0

Xem đáp án

Đáp án: C

Đường cao kẻ từ A của tam giác ABC là đường thẳng đi qua A và nhận vecto BC là vecto pháp tuyến

⇒ d: 2(x - 0) + (y + 3) = 0 ⇔ 2x + y + 3 = 0

Câu 14:

Phương trình của đường tròn (C) đi qua ba điểm A(0;4), B(2;4), C(4;0) có phương trình:

A. $x^{2}$ + $y^{2}$ - 8x + 2y - 1 = 0

B. $x^{2}$ + $y^{2}$ - 2x + 8y - 1 = 0

C. $x^{2}$ + $y^{2}$ - 2x - 2y - 8 = 0

D. $x^{2}$ + $y^{2}$ - 8x - 6y - 2 = 0

Xem đáp án

Đáp án: C

Giả sử (C) có dạng: $x^{2}$ + $y^{2}$ - 2ax - 2by + c = 0

Vì 3 điểm A, B, C thuộc đường tròn (C) nên ta có hệ phương trình:

Vậy phương trình đường tròn (C) có dạng: $x^{2}$ + $y^{2}$ - 2x - 2y - 8 = 0

Câu 15:

Phương trình của đường tròn (C) có đường kính AB với A(-1;2), B(1;4) là:

A. $x^{2}$ + (y - 3 $)^{2}$ = 2

B. $x^{2}$ + (y + 3 $)^{2}$ = 2

C. (x - 1 $)^{2}$ + (y - 1 $)^{2}$ = 3

D. (x - 1 $)^{2}$ + (y - 1 $)^{2}$ = 9

Xem đáp án

Đáp án: A

A(-1;2), B(1;4)

Gọi I là trung điểm của AB ⇒ I(0;3)

Đường tròn đường kính AB là đường tròn tâm I bán kính IA

⇒ (C): (x - 0 $)^{2}$ + (y - 3 $)^{2}$ = ( $\sqrt{2}$ $)^{2}$ ⇔ $x^{2}$ + (y - 3 $)^{2}$ = 2

Câu 16:

Với giá trị nào của m thì hai đường thẳng d1: 2x - 3y + 1 = 0 và $d_{2} : \{\begin{cases} x = 1 + 2 t \\ y = 7 - m t \end{cases}$ vuông góc với nhau?

A. $m = \frac{3}{2}$

B. m = 3

C. m = -3

D. $m = - \frac{3}{2}$

Xem đáp án

Đáp án: B

Câu 17:

Đường thẳng d đi qua điểm M(2;-3) và vuông góc với đường thẳng $d' : \{\begin{cases} x = 2 - t \\ y = 3 - 2 t \end{cases}, t \in ℝ$ có phương trình:

A. x + 2y + 4 = 0

B. 2x + 3y + 4 = 0

C. 2x - 3y + 1 = 0

D. x - 2y - 4 = 0

Xem đáp án

Đáp án: A

Vì d vuông góc với d’ nên d sẽ nhận vecto chỉ phương của d’ làm vecto pháp tuyến

Vậy d là đường thẳng đi qua M và có vecto pháp tuyến là

d: -1(x - 2) - 2(y + 3) = 0 ⇔ -x - 2y - 4 ⇔ x + 2y + 4 = 0

Câu 18:

Cho đường tròn (C): $x^{2}$ + $y^{2}$ - 2x + 6y + 8 = 0 và đường thẳng d: x + y + 4 = 0. Phương trình tiếp tuyến của đường tròn (C) và song song với đường thẳng d là:

A. $x + y - 4 = 0$

B. $[\begin{matrix} x + y = 0 \\ x + y + 4 = 0 \end{matrix}$

C. x + y = 0

D. x + y - 2 = 0

Xem đáp án

Đáp án: B

(C): $x^{2}$ + $y^{2}$ - 2x + 6y + 8 = 0

⇔ (x - 1 $)^{2}$ + (y + 3 $)^{2}$ = 2 có I(1;-3), R = $\sqrt{2}$

Gọi d’ là tiếp tuyến của đường tròn (C) và song song với d

Vì d'//d ⇒ d': x + y + c = 0, (c ≠ 4)

d’ là tiếp tuyến của (C) nên d(I;d') = R

Câu 19:

Xác định vị trí tương đối của hai đường thẳng d1: 2x - 3y + 2 = 0 và d2: 6x + 4y - 3 = 0

A. Song song

B. vuông góc

C. trùng nhau

D. cắt nhưng không vuông

Xem đáp án

Đáp án: B

Câu 20:

Phương trình tham số của đường thẳng đi qua hai điểm A(2;-1), B(3;2) là:

A. $\{\begin{cases} x = 3 + 3 t \\ y = 2 + t \end{cases}$

B. $\{\begin{cases} x = 2 + t \\ y = - 1 + 3 t \end{cases}$

C. $\{\begin{cases} x = 2 + 3 t \\ y = 1 - t \end{cases}$

D. $\{\begin{cases} x = 3 + t \\ y = 2 - 3 t \end{cases}$

Xem đáp án

Đáp án: B

Phương trình đường thẳng AB đi qua A nhận (AB) làm vecto chỉ phương:

Câu 21:

Phần II: Tự luận

Cho đường thẳng d: x - 2y - 3 = 0 và điểm M(2;3). Tìm điểm N là điểm đối xứng với M qua d?

Xem đáp án

d: x - 2y - 3 = 0 có

Gọi d’ là đường thẳng đi qua M và vuông góc với d

d': 2(x - 2) + (y - 3) = 0 ⇔ 2x + y - 7 = 0

Tọa độ giao điểm I của d và d’ là nghiệm của hệ phương trình:

Vì M và N đối xứng nhau qua d nên I là trung điểm của MN

Câu 22:

Viết phương trình đường tròn (C) có tâm I(2;-2) và tiếp xúc với đường thẳng x + y + 2 = 0?

Xem đáp án

Vì (C) tiếp xúc với đường thẳng d: x + y + 2 = 0 nên (C) có bán kính

Vậy đường tròn (C) có dạng: (x - 2 $)^{2}$ + (y + 2 $)^{2}$ = 2

Câu 23:

Viết phương trình tổng quát của đường thẳng cắt các trục tọa độ lần lượt tại hai điểm A và B sao cho tam giác OAB có trọng tâm G(1;3) với O là gốc tọa độ? Tính diện tích tam giác OAB?

Xem đáp án

Giả sử A(a;0), B(0;b)

Vì tam giác OAB có trọng tâm G(1;3) nên:

Phương trình AB có dạng:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Top 5 Đề kiểm tra 1 tiết Toán 10 Chương 3 Hình học có đáp án

Đề kiểm tra 45 phút Hình học 10 Chương 3 có đáp án (Đề 3)

Danh sách câu hỏi

Phần I: Trắc nghiệm

Phần II: Tự luận

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương