Dạng 1: Tứ giác có tổng hai góc đối nhau bằng 180 độ có đáp án
-
811 lượt thi
-
6 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC ( E khác B và C ), AE cắt CD tại F. Chứng minh BEFI là tứ giác nội tiếp đường tròn.

Tứ giác BEFI có:
BIF = 900 (giả thiết);
BEF = BEA = 900(góc nội tiếp chắn nửa đường tròn).
Suy ra tứ giác BEFI nội tiếp đường tròn đường kính BF.
Câu 2:
Cho nửa đường tròn (O) đường kính AB = 2R. Điểm C (khác A) bất kì nằm trên nửa đường tròn sao cho AC < CB. Điểm D thuộc cung nhỏ BC sao cho COD = 90o. Gọi E là giao điểm của AD và BC, F là giao điểm của AC và BD.
a) Chứng minh CEDF là tứ giác nội tiếp.
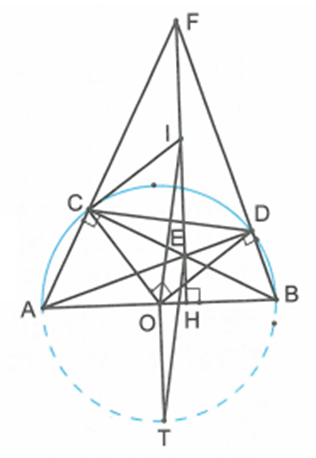
Ta có ACB = ADB = 90o (góc nội tiếp chắn nửa đường tròn)
=> FCE = FDE = 90o.
Tứ giác CEDF có FCE + FDE = 180o => CEDF là tứ giác nội tiếp.
Câu 3:
Chứng minh FC.FA = FB.FD.
Xét FCB và FDA có: FCB = FDA = 90o ;
CFD chung.
=> FCB và FDA (g.g) => (hai cạnh tương ứng).
=> FC.FA = FB.FD.
Câu 4:
c) Gọi I là trung điểm của EF. Chứng minh IC là tiếp tuyến của (O).
Gọi H là giao điểm của EF và AB. Vì E là trực tâm của ABF nên FH AB.
OCA cân tại O nên OCA = OAC (hai góc ở đáy).
Ta có CI là đường trung tuyến của tam giác vuông CEF nên CIB = CF. Do đó ICF cân tại I nên ICF = IFC (hai góc ở đáy).
=> ICF + OCA = IFC + OAC = 90 (vì HAF vuông tại H).
=> ICO = 90 => IC OC. Vậy IC là tiếp tuyến của đường tròn (O).
Câu 5:
Gọi T là điểm chính giữa của cung AB không chứa điểm C (T cố định).
Khi đó OT AB nên OT // IE.
Chứng minh tương tự câu c, ta có được ID là tiếp tuyến của đường tròn (O).
Do đó tứ giác ICOD là hình chữ nhật. Lại có OC = OD nên tứ giác này là hình vuông cạnh R.
Tam giác ECF vuông tại C có CI là trung tuyến nên IE = CI = R.
Ta có: OT // IE và OT = IE = R nên IETO là hình bình hành.
Do vậy TE = OI = R.
Vậy E thuộc đường tròn tâm T bán kính R.
Câu 6:
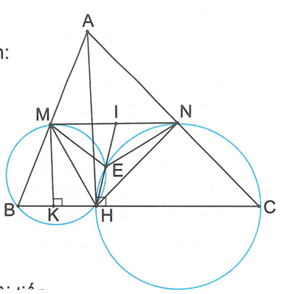
Cho tam giác ABC và đường cao AH. Gọi M, N lần lượt là trung điểm của AB, AC. Đường tròn ngoại tiếp tam giác BHM cắt đường tròn ngoại tiếp tam giác CNH tại E. Chứng minh AMEN là tứ giác nội tiếp và HE đi qua trung điểm của MN.
Ta có: MEN = 360 - ( MEH + NEH )
= 360 - ( 180 - ABC + 180 - ACB)
= ABC + ACB = 180 - BAC
Suy ra MEN + MAN = 180 hay tứ giác AMEN là tứ giác nội tiếp.
Kẻ MK BC, giả sử HE cắt MN tại I thì IH là cát tuyến của hai đường tròn (BMH), (CNH).
Lại có MB = MH = MA (tính chất trung tuyến tam giác vuông). Suy ra tam giác MBH cân tại M.
=> KB = KH => MK luôn đi qua tâm đường tròn ngoại tiếp tam giác MBH.
Hay MN là tiếp tuyến của (MBH) suy ra IM2= IE.IH (1)
Tương tự ta cũng có MN là tiếp tuyến của (HNC) suy ra IN2= IE.IH. (2)
Từ (1) và (2) suy ra IM = IN.
Vậy HE đi qua trung điểm của MN.
