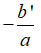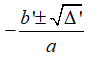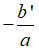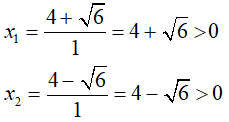Trắc nghiệm Toán 9 Bài 5 (có đáp án): Công thức nghiệm thu gọn
-
1126 lượt thi
-
10 câu hỏi
-
10 phút
Danh sách câu hỏi
Câu 1:
Cho phương trình a + bx + c = 0 (a 0) có biệt thức b = 2b'; ' = - ac. Phương trình đã cho có hai nghiệm phân biệt khi:
Đáp án A
Xét phương trình bậc hai a + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = - ac:
• TH1: Nếu Δ' < 0 thì phương trình vô nghiệm
• TH2: Nếu Δ' = 0 thì phương trình có nghiệm kép = =
• TH3: Nếu Δ' > 0 thì phương trình có hai nghiệm phân biệt =
Câu 2:
Cho phương trình a + bx + c = 0 (a 0) có biệt thức b = 2b'; ' = - ac. Nếu ' = 0 thì:
Đáp án C
Xét phương trình bậc hai a + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = - ac:
Nếu Δ' = 0 thì phương trình có nghiệm kép = =
Câu 3:
Tính ' và tìm số nghiệm của phương trình 7 - 12x + 4 = 0
Đáp án B
Phương trình có a = 7; b' = -6; c = 4 suy ra:
Nên phương trình có hai nghiệm phân biệt.
Câu 6:
Tìm nghiệm dương của phương trình: - 8x + 10 = 0
Đáp án D
Ta có: a = 1; b = - 8 nên b’ = -4; c = 10.
' = - 1.10 = 16 - 10 = 6
Do đó, phương trình đã cho có hai nghiệm phân biệt là;
Vậy cả hai nghiệm trên đều là nghiệm dương của phương trình đã cho.
Câu 7:
Cho phương trình 2 - 10x + m + 1 = 0; ( m là tham số). Tìm m để biệt thức ' = 11
Đáp án B
Ta có: a = 2 ; b = -10 nên b’ = -5; c = m + 1
Để
⇔ -2m = -12 ⇔ m = 6
Câu 8:
Cho phương trình 2 – 4x + m = 0. Tìm m để phương trình trên vô nghiệm?
Đáp án C
Ta có: a = 2; b = - 4 nên b’ = -2 và c = m
Để phương trình đã cho vô nghiệm thì:4 – 2m < 0 hay m > 2.
Câu 9:
Cho hai phương trình – 4x + 4= 0 và + (m + 1)x + m = 0 . Tìm m để hai phương trình trên có nghiệm chung?
Đáp án D
* Xét phương trình :
Vậy phương trình này có nghiệm duy nhất.
Để hai phương trình đã cho có nghiệm chung khi và chỉ khi x = 2 là nghiệm phương trình
.Suy ra:
⇔ 4 + 2m + 2 + m = 0 ⇔ 6 + 3m = 0
⇔ 3m = -6 ⇔ m = -2
Câu 10:
Cho phương trình . Tìm m để phương trình chỉ có một nghiệm.
Đáp án B
Ta có
Để phương trình có một nghiệm thì