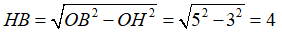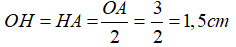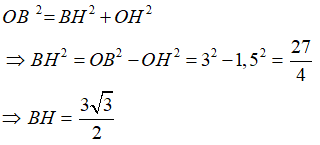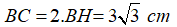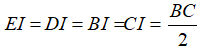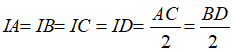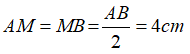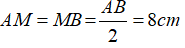Trắc nghiệm Toán 9 Bài 2 (có đáp án): Đường kính và dây của đường tròn
-
973 lượt thi
-
10 câu hỏi
-
15 phút
Danh sách câu hỏi
Câu 1:
Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng?
Đáp án A.
Trong các dây của đường tròn, dây lớn nhất là đường kính
Câu 2:
Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết rằng khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng
Đáp án B.
Trong một đường tròn: Hai dây cách đều tâm thì bằng nhau
Câu 3:
“Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì…với dây ấy”. Điền vào dấu…cụm từ thích hợp
Đáp án D
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy
Câu 4:
Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn
Đáp án A
Trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm
- Trong hai dây của đường tròn:
+ Dây nào lớn hơn thì dây đó gần tâm hơn
+ Dây nào gần tâm hơn thì dây đó lớn hơn
Nên phương án B, C, D đúng
Câu 5:
Cho đường tròn (O) có bán kính R = 5 cm. Khoảng cách từ tâm đến dây AB là 3 cm. Tính độ dài dây AB
Đáp án B
Kẻ OH ⊥ AB tại H suy ra H là trung điểm của AB
Xét tam giác OHB vuông tại H có OH = 3; OB = 5 . Theo định lý Pytago ta có:
Mà H là trung điểm của AB nên AB = 2HB = 8 cm
Vậy AB = 8 cm
Câu 6:
Cho đường tròn (O) có bán kính OA = 3cm. Dây BC của đường tròn vuông góc với OA tại trung điểm của OA. Tính BC.
Đáp án A
Gọi H là trung điểm của BC.
Do dây BC vuông góc với OA tại H nên ta có:
Áp dụng định lí Pytgo vào tam giác OHB vuông tại H ta có:
Theo định lí quan hệ vuông góc đường kính và dây ta có: H là trung điểm BC nên:
Câu 7:
Cho ΔABC, các đường cao BD và CE. Tìm mệnh đề sai
Đáp án D
Gọi I là trung điểm BC.
Tam giác BCE vuông tại E có đường trung tuyến EI ứng với cạnh huyền BC nên:
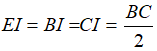
Tam giác BCD vuông tại D có DI là đường trung tuyến ứng với cạnh huyền BC nên:
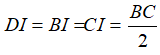
Từ ( 1) và (2) suy ra:
Do đó, I là tâm đường tròn ngoại tiếp tứ giác BCDE.
Khi đó, BC là đường kính và DE là dây không đi qua tâm nên: BC > DE.
Câu 8:
Cho hình chữ nhật ABCD. Tìm khẳng định đúng
Đáp án C
Gọi I là giao điểm hai đường chéo AC và BD,
Theo tính chất hình chữ nhật ta có:
Do đó, I là tâm đường tròn ngoại tiếp hình chữ nhật ABCD có AC và BD là đường kính.
AB, BC, CD và DA là các dây.
Câu 9:
Cho đường tròn tâm O , bán kính R = 5cm , có dây AB = 8cm và M là trung điểm của AB. Tính khoảng cách từ O đến AB?
Đáp án A
Vì M là trung điểm của AB nên ta có:
Theo quan hệ vuông góc giữa đường kính và dây ta có:
OM ⊥ AB
Áp dụng định lí Pytago vào tam giác OAM ta có:
Câu 10:
Cho đường tròn tâm O có dây AB = 16cm. Gọi M là trung điểm AB. Biết khoảng cách từ O đến AB bằng 6. Tính bán kính đường tròn.
Đáp án C
Vì M là trung điểm của AB nên ta có:
Theo quan hệ vuông góc giữa đường kính và dây ta có;
Mà khoảng cách từ O đến AM bằng 6 cm nên OM = 6 cm
Áp dụng định lí pytago vào tam giác OAM vuông ta có:
Suy ra: bán kính đường tròn đã cho là R = 10 cm.