20 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 29 - qa.haylamdo.com

Bài tập theo tuần Toán 9 - Tuần 29

Đề số 1

Bài tập theo tuần Toán 9 - Tuần 29

351 lượt thi
20 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho phương trình $(m + 1) x^{2} - 2 (m + 1) x + m - 2 = 0 (1)$ (m là tham số)

a) Giải phương trình (1) với m = 3

b) Tìm các giá trị của m để phương trình (1) có hai nghiệm thỏa : $\frac{1}{x_{1}} + \frac{1}{x_{2}} = \frac{3}{2}$

$(m + 1) x^{2} - 2 (m + 1) x + m - 2 = 0 (1) (m \neq - 1)$

a) Khi m = 3, phương trình (1) thành $4 x^{2} - 8 x + 1 = 0$

$Δ' = 4^{2} - 4.1 = 12 > 0$ nên phương trình có hai nghiệm

$[\begin{array}{l} x_{1} = \frac{4 + \sqrt{12}}{4} = \frac{2 + \sqrt{3}}{2} \\ x_{2} = \frac{4 - \sqrt{12}}{4} = \frac{2 - \sqrt{3}}{2} \end{array}$

b) Để phương trình có 2 nghiệm thì (1) có $Δ' \geq 0$

$\begin{array}{l} \Leftrightarrow {(m + 1)}^{2} - (m + 1) (m - 2) \geq 0 \\ \Leftrightarrow m^{2} + 2 m + 1 - m^{2} + m + 2 \geq 0 \Leftrightarrow m \geq - 1 \end{array}$

Kết hợp với điều kiện trên $\Rightarrow m > - 1,$ khi đó, áp dụng Vi et :

$\{\begin{cases} x_{1} + x_{2} = \frac{2 (m + 1)}{m + 1} = 2 \\ x_{1} x_{2} = \frac{m - 2}{m + 1} \end{cases}$ . Ta có:

$\frac{1}{x_{1}} + \frac{1}{x_{2}} = \frac{3}{2} \Leftrightarrow \frac{x_{1} + x_{2}}{x_{1} x_{2}} = \frac{3}{2}$

$h a y \frac{2}{\frac{m - 2}{m + 1}} = \frac{3}{2} \Leftrightarrow \frac{3 m - 6}{m + 1} = 4 \Leftrightarrow 3 m - 6 = 4 m + 4 \Leftrightarrow m = - 10 (k t m)$

Vậy không có m thỏa đề.

Câu 2:

Cho phương trình : $m x^{2} - (2 m + 3) x + m - 4 = 0$

Tìm m để phương trình có hai nghiệm phân biệt

$m x^{2} - (2 m + 3) x + m - 4 = 0 (2)$

$Δ = {(2 m + 3)}^{2} - 4 m (m - 4) = 24 m + 9$

Để phương trình (2) có hai nghiệm phân biệt

\Leftrightarrow Δ > 0 \Leftrightarrow 24 m + 9 > 0 \Leftrightarrow m > - \frac{3}{8}

Câu 3:

Cho phương trình :

m x^{2} - (2 m + 3) x + m - 4 = 0

Tìm hệ thức độc lập không phụ thuộc tham số m

$m x^{2} - (2 m + 3) x + m - 4 = 0 (2)$

Khi đó áp dụng Vi – et $\Rightarrow \{\begin{cases} x_{1} + x_{2} = \frac{2 m + 3}{m} (a) \\ x_{1} x_{2} = m - 4 (b) \end{cases}$

$(b) \Rightarrow m = x_{1} x_{2} + 4$ . Thay (b) vào (a) ta được :

$x_{1} + x_{2} = \frac{2 x_{1} x_{2} + 8 + 3}{x_{1} x_{2} + 4} \Leftrightarrow x_{1} + x_{2} = \frac{2 x_{1} x_{2} + 11}{x_{1} x_{2} + 4}$

Đây là phương trình độc lập với m

Câu 4:

Cho parabol $(P) : y = - x^{2}$ và đường thẳng $(d) : y = m x - 2$ (m là tham số). Tìm tất cả các giá trị của tham số m để đường thẳng (d) cắt parabol (P) tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ thỏa mãn $(x_{1} + 2) (x_{2} + 2) = 0$

Ta có phương trình hoành độ giao điểm :

$- x^{2} = m x - 2 \Leftrightarrow x^{2} + m x - 2 = 0$

$Δ = m^{2} + 8 > 0$ (với mọi m) nên phương trình luôn có hai nghiệm phân biệt

Áp dụng định lý Vi – et $\Rightarrow \{\begin{cases} x_{1} + x_{2} = - m \\ x_{1} x_{2} = - 2 \end{cases}$

Ta có:

\begin{array}{l} (x_{1} + 2) (x_{2} + 2) + 4 = 0 \Leftrightarrow x_{1} x_{2} + 2 (x_{1} + x_{2}) + 4 = 0 \\ h a y - 2 + 2 (- m) + 4 = 0 \Leftrightarrow m = 1 \end{array}

Câu 5:

Cho phương trình $m x^{2} - 2 (m + 1) x + 4 m = 0$ (m là tham số, $m \neq 0)$

Tìm m để phương trình có nghiệm kép

$m x^{2} - 2 (m + 1) x + 4 m = 0 (m \neq 0)$

$Δ' = {(m + 1)}^{2} - m .4 m = - 3 m^{2} + 2 m + 1$

Để phương trình có nghiệm kép

\Leftrightarrow Δ' = 0 \Leftrightarrow - 3 m^{2} + 2 m + 1 = 0 \Leftrightarrow [\begin{array}{l} m = 1 \\ m = - \frac{1}{3} \end{array}

Câu 6:

Cho phương trình

m x^{2} - 2 (m + 1) x + 4 m = 0

(m là tham số,

m \neq 0)

Tìm m để phương trình có hai nghiệm $x_{1}, x_{2}$ thỏa mãn $x_{1}^{2} + x_{2}^{2} - 17 = 0$

$m x^{2} - 2 (m + 1) x + 4 m = 0 (m \neq 0)$

Để phương trình có nghiệm $\Leftrightarrow Δ' \geq 0 \Leftrightarrow - 3 m^{2} + 2 m + 1 \geq 0 \Leftrightarrow \frac{- 1}{3} \leq m \leq 1$ và $m \neq 0$

Áp dụng định lý Viet $\{\begin{cases} x_{1} + x_{2} = \frac{2 m + 1}{m} \\ x_{1} x_{2} = 4 \end{cases}$ . Ta có:

$\begin{array}{l} x_{1}^{2} + x_{2}^{2} - 17 = 0 \Leftrightarrow {(x_{1} + x_{2})}^{2} - 2 x_{1} x_{2} - 17 = 0 \\ h a y \frac{{(2 m + 1)}^{2}}{m^{2}} - 8 - 17 = 0 \Leftrightarrow 4 m^{2} + 4 m + = 25 m^{2} \\ \Leftrightarrow - 21 m^{2} + 4 m + 1 = 0 \Leftrightarrow [\begin{array}{l} m = \frac{1}{3} \\ m = - \frac{1}{7} \end{array} (t m) \end{array}$

Vậy $m \in \{\frac{1}{3}; - \frac{1}{7}\}$ thì thỏa đề .

Câu 7:

Cho phương trình $x^{2} - (m + 3) x - 2 m^{2} + 2 = 0 (m$ là tham số)

Tìm các giá trị của m để hệ thức

3 x_{1} + 2 x_{2} = 8

$x^{2} - (m + 3) x - 2 m^{2} + 2 = 0$

$\begin{array}{l} Δ = {(m + 3)}^{2} - 4.1. (- 2 m^{2} + 2) = m^{2} + 6 m + 9 + 8 m^{2} - 8 \\ = 9 m^{2} + 6 m + 1 = {(3 m + 1)}^{2} \geq 0 (v o i m o i m) \end{array}$

Nên phương trình luôn có nghiệm . Áp dụng Vi – et :

$\{\begin{cases} x_{1} + x_{2} = m + 3 \\ x_{1} x_{2} = 2 - 2 m^{2} \end{cases}$

kết hợp với

3 x_{1} + 2 x_{2} = 8

. Ta có:

\{\begin{cases} x_{1} + x_{2} = m + 3 \\ 3 x_{1} + 2 x_{2} = 8 \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = 2 - 2 m \\ x_{2} = 3 m + 1 \end{cases}

Thay vào $x_{1} x_{2} = 2 - 2 m^{2}$ ta được:

$\begin{array}{l} (2 - 2 m) (3 m + 1) = 2 - 2 m^{2} \\ \Leftrightarrow - 6 m^{2} + 4 m + 2 - 2 + 2 m^{2} = 0 \\ \Leftrightarrow - 4 m^{2} + 4 m = 0 \Leftrightarrow 4 m (1 - m) = 0 \\ \Leftrightarrow [\begin{array}{l} m = 0 \\ m = 1 \end{array} \end{array}$

Vậy m = 0, m = 1 thỏa đề.

Câu 8:

Cho phương trình $x^{2} - (2 m + 1) x + m^{2} + m - 6 = 0$ (m là tham số)

Chứng minh phương trình luôn có hai nghiệm phân biệt

$x^{2} - (2 m + 1) x + m^{2} + m - 6 = 0$

$Δ = {(2 m + 1)}^{2} - 4 (m^{2} + m - 6) = 25 > 0$

nên phương trình luôn có hai nghiệm phân biệt

Câu 9:

Cho phương trình

x^{2} - (2 m + 1) x + m^{2} + m - 6 = 0

(m là tham số)

Tìm các giá trị tham số m để phương trình có hai nghiệm âm phân biệt

$x^{2} - (2 m + 1) x + m^{2} + m - 6 = 0$

Để phương trình có 2 nghiệm âm phân biệt

\Rightarrow \{\begin{cases} S < 0 \\ P > 0 \end{cases} \Leftrightarrow \{\begin{cases} 2 m + 1 < 0 \\ m^{2} + m - 6 > 0 \end{cases} \Leftrightarrow \{\begin{cases} m < - \frac{1}{2} \\ [\begin{array}{l} m < - 3 \\ m > - \frac{1}{2} \end{array} \end{cases} \Leftrightarrow m < - 3

Câu 10:

Cho phương trình $x^{2} - (2 m + 1) x + m^{2} + m - 6 = 0$ (m là tham số)

Gọi $x_{1}, x_{2}$ là hai nghiệm của phương trình . Tìm giá trị nhỏ nhất của biểu thức $A = x_{1}^{2} + x_{2}^{2}$

$\begin{array}{l} x_{1}^{2} + x_{2}^{2} = {(x_{1} + x_{2})}^{2} - 2 x_{1} x_{2} = {(2 m + 1)}^{2} - 2 (m^{2} + m - 6) \\ = 4 m^{2} + 4 m + 1 - 2 m^{2} - 2 m + 12 = 2 m^{2} + 2 m + 13 \\ = 2 (m^{2} + m + \frac{13}{2}) = 2 [{(m + \frac{1}{2})}^{2} + \frac{25}{4}] \\ = 2. {(m + \frac{1}{2})}^{2} + \frac{25}{2} \end{array}$

Vì $2 {(m + \frac{1}{2})}^{2} \geq 0$ (với mọi m) nên $2 {(m + \frac{1}{2})}^{2} + \frac{25}{2} \geq \frac{25}{2}$

$\Rightarrow M i n A = \frac{25}{2} \Leftrightarrow m = - \frac{1}{2}$

Câu 11:

Cho phương trình $x^{2} - (2 m + 1) x + m^{2} + m - 6 = 0$ (m là tham số)

Tìm các giá trị của m để phương trình có hai nghiệm $x_{1}, x_{2}$ thỏa mãn $|x_{1}^{3} + x_{2}^{3}| = 19$

$\begin{array}{l} \{\begin{cases} x_{1} + x_{2} = 2 m + 1 \\ x_{1} x_{2} = m^{2} + m - 6 \end{cases} \\ |x_{1}^{3} + x_{2}^{3}| = 19 \Leftrightarrow |(x_{1} + x_{2}) (x_{1}^{2} - x_{1} x_{2} + x_{2}^{2})| = 19 \\ \Leftrightarrow |(x_{1} + x_{2}) [{(x_{1} + x_{2})}^{2} - 3 x_{1} x_{2}]| = 19 \\ {(2 m + 1)}^{2} [{(2 m + 1)}^{2} - 3 (m^{2} + m - 6)] = 19 \\ \Leftrightarrow (4 m^{2} + 4 m + 1) (m^{2} + m + 19) = 19 \end{array}$

Đặt $t = m^{2} + m,$ phương trình thành:

$(4 t + 1) (t + 19) = 19 \Leftrightarrow 4 t^{2} + 77 t = 0 \Leftrightarrow [\begin{array}{l} t = 0 \\ t = - \frac{77}{4} \end{array}$

$\begin{array}{l} *) t = 0 \Rightarrow m^{2} + m = 0 \Leftrightarrow [\begin{array}{l} m = 0 \\ m = - 1 \end{array} \\ *) t = \frac{- 77}{4} \Rightarrow m^{2} + m + \frac{77}{4} = 0 (V N) \end{array}$

Vậy $m \in \{0; - 1\}$ thỏa đề

Câu 12:

Tìm hai số u, v trong trường hợp sau :

$u + v = 15, u v = 36$

u, v là hai nghiệm phương trình $X^{2} - 15 X + 36 \Leftrightarrow [\begin{array}{l} X_{1} = 12 \\ X_{2} = 3 \end{array}$

Vậy $(u, v) \in \{(12; 3); (3; 12)\}$

Câu 13:

Tìm hai số u, v trong trường hợp sau :

$u^{2} + v^{2} = 13, u v = 6$

$\begin{array}{l} u^{2} + v^{2} = 13, u v = 6 \\ u^{2} + v^{2} = 13 \Leftrightarrow {(u + v)}^{2} - 2 u v = 13 \Leftrightarrow {(u + v)}^{2} = 13 + 2.6 = 25 \\ \Rightarrow [\begin{array}{l} u + v = 5 \\ u + v = - 5 \end{array} \end{array}$

$*) u + v = 5 \Rightarrow u, v$ là nghiệm phương trình: $X^{2} - 5 X + 6 = 0 \Rightarrow [\begin{array}{l} X = 3 \\ X = 2 \end{array}$

$*) u + v = - 5 \Rightarrow u, v$ là nghiệm phương trình $X^{2} + 5 X + 6 = 0 \Leftrightarrow [\begin{array}{l} X = - 2 \\ X = - 3 \end{array}$

Vậy $(u, v) \in \{(3; 2); (2; 3); (- 2; - 3); (- 3; - 2)\}$

Câu 14:

Tìm hai số u, v trong trường hợp sau :

$u + v = 4, u v = 7$

$u + v = 4, u v = 7, u, v$ là nghiệm phương trình $X^{2} - 4 X + 7 = 0 \Rightarrow P T V N$

Vậy không có u, v thỏa đề.

Câu 15:

Tìm hai số u, v trong trường hợp sau :

$u + v = - 12, u v = 20$

$u + v = - 12, u v = 20, u, v$ là nghiệm phương trình $X^{2} + 12 X + 20 \Leftrightarrow [\begin{array}{l} X = - 2 \\ X = - 10 \end{array}$

Vậy $(u, v) \in \{(- 2; - 10); (- 10; - 2)\}$

Câu 16:

Cho phương trình $x^{2} - 2 (m + 1) x + m^{2} - 3 = 0 (1)$

a) Giải phương trình (1) với m = 3

b) Tìm các giá trị của m để phương trình (1) có hai nghiệm $x_{1}, x_{2}$ thỏa : $x_{1}^{2} + x_{2}^{2} - 2 x_{1} x_{2} > 3$

$x^{2} - 2 (m + 1) x + m^{2} - 3 = 0 (1)$

a) Khi m = 3 phương trình (1) thành :

$x^{2} - 8 x + 6 \Rightarrow x = 4 \pm \sqrt{10}$

b) $Δ' = {(m + 1)}^{2} - (m^{2} - 3) = 2 m + 4$

Để phương trình (1) có nghiệm phân biệt $\Leftrightarrow Δ' > 0 \Leftrightarrow 2 m + 4 > 0 \Leftrightarrow m > - 2$

Khi đó, áp dụng Vi – et $\{\begin{cases} x_{1} + x_{2} = 2 m + 2 \\ x_{1} x_{2} = m^{2} - 3 \end{cases}$ . Ta có:

$x_{1}^{2} + x_{2}^{2} - 2 x_{1} x_{2} > 3 \Leftrightarrow {(x_{1} + x_{2})}^{2} - 4 x_{1} x_{2} > 3$

$\begin{array}{l} h a y {(2 m + 2)}^{2} - 4. (m^{2} - 3) > 3 \\ \Leftrightarrow 4 m^{2} + 8 m + 4 - 4 m^{2} + 12 > 3 \\ \Leftrightarrow 8 m > - 13 \Leftrightarrow m > \frac{- 13}{8} (t m) \end{array}$

Vậy $m > \frac{- 13}{8}$ thì thỏa đề

Câu 17:

Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O (AB < AC). Hai tiếp tuyến tại B và C cắt nhau tại M, AM cắt (O) tại điểm thứ hai là D. Gọi E là trung điểm AD, EC cắt (O) tại điểm thứ hai là F. Chứng minh :

a) Tứ giác OEBM nội tiếp

b) $M B^{2} = M A . M D$

$c) ∠ B F C = ∠ M O C d) B F / / A M$

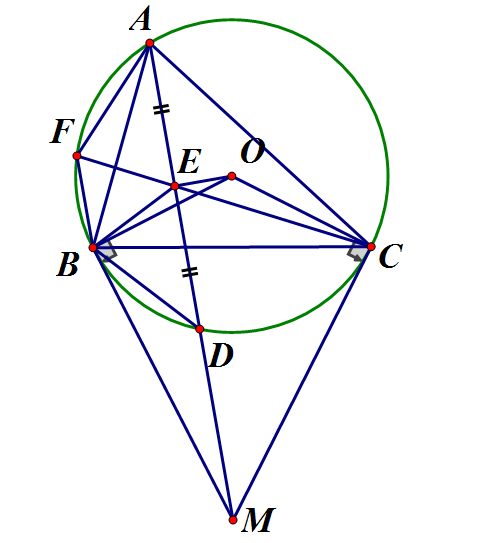
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O (AB < AC). Hai tiếp (ảnh 1)

$a) ∠ O B M = ∠ O E M = 90^{0} \Rightarrow O E B M$ là tứ giác nội tiếp

b) Chứng minh được $Δ A B M = Δ B D M (g - g) \Rightarrow M B^{2} = M A . M D$

c) $Δ O B C$ cân tại O có OM vừa là đường trung trực vừa là đường phân giác

$\Rightarrow ∠ M O C = \frac{1}{2} ∠ B O C = \frac{1}{2} s d \overset{⏜}{B C}$

Mà $∠ B F C = \frac{1}{2} s d \overset{⏜}{B C} \Rightarrow ∠ M O C = ∠ B F C$

$d) ∠ O E M = ∠ O C M = 90^{0} \Rightarrow E O C M$ là tứ giác nội tiếp

$\Rightarrow ∠ M E C = ∠ M O C = ∠ B F C$ mà hai góc ở vị trí đồng vị nên FB // AM

Câu 18:

Cho tam giác ABC có $∠ B A C = 45^{0} .$ Các góc B, C đều nhọn. Đường tròn đường kính BC cắt AB, AC lần lượt tại D và E. Gọi H là giao điểm CD và BE

a) Chứng minh AE = BE

b) Chứng minh ADHE là tứ giác nội tiếp. Xác định tâm K của đường tròn ngoại tiếp này.

c) Chứng minh OE là tiếp tuyến của đường tròn ngoại tiếp $Δ A D E$

d) Cho BC = 2a. Tính diện tích viên phân cung $\overset{⏜}{D E}$ của đường tròn (O) theo a

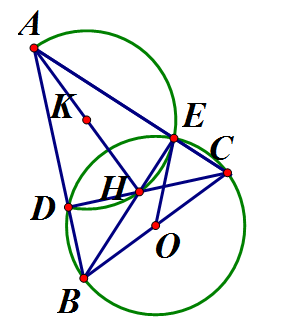
Cho tam giác ABC có góc BAC = 45 độ. Các góc B, C đều nhọn. Đường tròn đường (ảnh 1)

a) Chứng minh: AE = BE

Ta có : $∠ B E A = 90^{0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow ∠ A E B = 90^{0}$

$Δ A E B$ vuông ở E có $∠ B A E = 45^{0}$ nên vuông cân $\Rightarrow A E = B E$

b) $∠ B D C = 90^{0} \Rightarrow ∠ A D H = 90^{0}$

Tứ giác ADHE có $∠ A D H + ∠ A E H = 180^{0}$ nên nội tiếp đường tròn, tâm K của đường tròn này là trung điểm AH

c) $Δ A E H$ vuông ở E có K là trung điểm AH nên $K E = K A = \frac{1}{2} A H$

Vậy $Δ A K E$ cân ở K. Do đó $∠ K A E = ∠ K E A$

$Δ E O C$ cân ở O (do $O C = O E) \Rightarrow ∠ O C E = ∠ O E C \Rightarrow H$ là trực tâm $Δ A B C \Rightarrow A H ⊥ B C$

$∠ H A C + ∠ A C O = 90^{0} \Rightarrow ∠ A E K + ∠ O E C = 90^{0}$

Do đó $∠ K E O = 90^{0} \Rightarrow O E ⊥ K E$

Điểm K là tâm đường tròn ngoại tiếp tứ giác ADHE nên cũng là tâm đường tròn ngoại tiếp $Δ A D E$

Vậy OE là tiếp tuyến đường tròn ngoại tiếp $Δ A D E$

d) Ta có : $∠ D O E = 2 ∠ A B E = {2.45}^{0} = 90^{0}$ (cùng chắn cung DE)

$\Rightarrow S_{q u a t (D O E)} = \frac{π a^{2} {.90}^{0}}{360^{0}} = \frac{π a^{2}}{4}$ ; $S_{D O E} = \frac{1}{2} O D . O E = \frac{1}{2} a^{2}$

Vậy diện tích viên phân cung DE là :

\frac{π a^{2}}{4} - \frac{a^{2}}{2} = \frac{a^{2}}{4} (π - 2)

Câu 19:

Cho nửa đường tròn tâm (O) đường kính BC = 2a và một điểm A nằm trên nửa đường tròn sao cho AB = a. Trên cung AC lấy điểm M, BM cắt AC tại I. Tia BA cắt đường thẳng CM tại D

a) Chứng minh $Δ A O B$ là tam giác đều

b) Chứng minh tứ giác AIMD nội tiếp đường tròn, xác định tâm K của đường tròn ngoại tiếp tứ giác đó

c) Cho $∠ A B M = 45^{0} .$ Tính độ dài cung AI và $S_{q u a t}$ AKI của đường tròn tâm K theo a

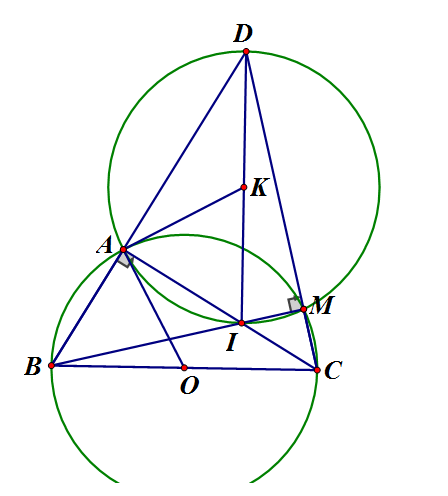
Cho nửa đường tròn tâm (O) đường kính BC = 2a và một điểm A nằm trên nửa (ảnh 1)

a) $Δ O A B$ có $O A = O B = A B = a \Rightarrow Δ O A B$ đều

b) $∠ B A C = ∠ B M C = \frac{1}{2} s d \overset{⏜}{B C} = 90^{0}$

$\Rightarrow ∠ C A D = ∠ B M D = 90^{0} \Rightarrow ∠ I A D + ∠ I M D = 180^{0}$

$\Rightarrow A I M D$ nội tiếp đường tròn đường kính DI, tâm I là trung điểm DI

$∠ A B M = 45^{0} \Rightarrow Δ A B I$ vuông cân tại $A \Rightarrow A I = A B = a$

AIMD nội tiếp $\Rightarrow ∠ A D I = ∠ A M I = \frac{1}{2} ∠ A O B = 30^{0}$

$\Rightarrow D I = 2 A I = 2 a; A K = K I = \frac{1}{2} D I = a$ $\Leftrightarrow Δ A K I$ đều $\Rightarrow ∠ A K I = 60^{0}$

c) $l_{\overset{⏜}{A I}} = \frac{2 π a {.60}^{0}}{360^{0}} = \frac{π a}{3}$ ; $S_{q u a t (A K I)} = \frac{π a^{2} {.60}^{0}}{360^{0}} = \frac{π a^{2}}{6}$

Câu 20:

Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao BD, CE của tam giác cắt nhau tại H $(D \in A C, E \in A B)$

a) Chứng minh tứ giác AEHD nội tiếp. Từ đó suy ra $∠ B C D = ∠ A E D$

b) Kẻ đường kính AK. Chứng minh $A B . B C = A K . B D$

c) Từ O kẻ $O M ⊥ B C (M \in B C) .$ Chứng minh H, M, K thẳng hàng.

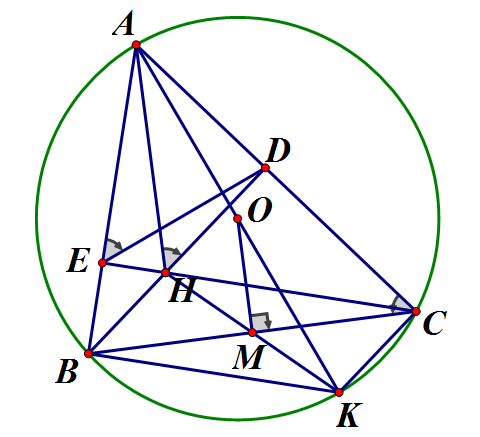
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao BD (ảnh 1)

a) Ta có $∠ A E H = ∠ A D H = 90^{0} \Rightarrow A E H D$ là tứ giác nội tiếp

$\Rightarrow ∠ A E D = ∠ A H D$ (cùng chắn $\overset{⏜}{A D})$

Lý luận được $∠ A C B = ∠ A H D$ (cùng phụ $∠ C A H) \Rightarrow ∠ A E D = ∠ A H D$ )

b) Xét $Δ A B K$ và $Δ B D C$ có: $∠ A B K = ∠ B D C = 90^{0}$ ;

$∠ A K B = ∠ B C D$ (cùng chắn $\overset{⏜}{A B}) \Rightarrow Δ A B K ~ Δ B D C (g . g)$

$\Rightarrow \frac{A B}{B D} = \frac{A K}{B C} \Rightarrow A B . B C = A K . B D$

c) Ta có : $O M ⊥ B C \Rightarrow M$ là trung điểm BC

Vì $B D / / K C (⊥ A C), B K / / H C (⊥ A B)$

$\Rightarrow H C K B$ là hình bình hành $\Rightarrow$ HK đi qua trung điểm M của BC

Vậy 3 điểm H, M, K thẳng hàng.

Bắt đầu thi ngay

Có thể bạn quan tâm

Các bài thi hot trong chương