27 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 9 Bài 4 (có đáp án): Một số hệ thức về cạnh và góc trong tam giác vuông (phần 2)

Câu 1:

Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?

A. MN = MP. sin P

B. MN = MP. cos P

C. MN = MP. tan P

D. MN = MP. cot P

Xem đáp án

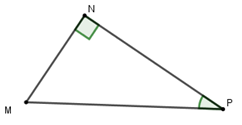
Ta có sin P = $\frac{M N}{M P}$ => MN = MP. sin P

Đáp án cần chọn là: A

Câu 2:

Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?

A. NP = MP. sin P

B. NP = MN. cot P

C. NP = MN. tan P

D. NP = MP. cot P

Xem đáp án

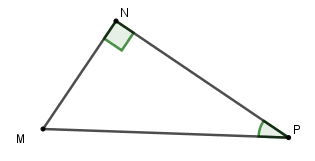
Ta có cot P = $\frac{N P}{M N}$ => NP = MN. cot P

Đáp án cần chọn là: B

Câu 3:

Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Chọn khẳng định sai?

A. b = a.sin B = a.cos C

B. a = c.tan B = c.cot C

C. $a^{2} = b^{2} + c^{2}$

D. c = a.sin C = a.cos B

Xem đáp án

Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Ta có:

+) Theo định lý Py-ta-go ta có $a^{2} = b^{2} + c^{2}$ nên C đúng.

+) Theo hệ thức về cạnh và góc trong tam giác vuông ta có:

b = a.sin B = a.cos C; c = a.sin C = a.cos B; b = c.tan B = c.cot C;

C = b.tan C = b.cot B

Nên A, D đúng

Đáp án cần chọn là: B

Câu 4:

Cho tam giác ABC vuông tại A có BC = a, AC = b, $\hat{A B C} = 50^{0}$ . Chọn khẳng định đúng.

A. b = c.sin $50^{0}$ .

B. b = a.tan $50^{0}$ .

C. b = c.cot $50^{0}$ .

D. c = b.cot $50^{0}$ .

Xem đáp án

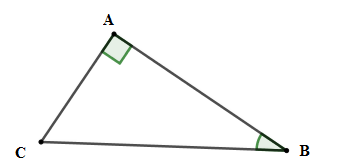
Cho tam giác ABC vuông tại A BC = a, AC = b, AB = c.

+) Theo hệ thức về cạnh và góc trong tam giác vuông ta có:

b = a.sin B = a.sin $50^{0}$ ;

c = a.cos B = a.cos $50^{0}$ ;

b = c.tan $50^{0}$ ;

c = b.cot $50^{0}$ .

Nên D đúng

Đáp án cần chọn là: D

Câu 5:

Cho tam giác ABC vuông tại A có AC = 10cm, $\hat{C} = 30^{0}$ . Tính AB, BC

A. AB = $\frac{5 \sqrt{3}}{3}$ ; BC = $\frac{20 \sqrt{3}}{3}$

B. AB = $\frac{10 \sqrt{3}}{3}$ ; BC = $\frac{14 \sqrt{3}}{3}$

C. AB = $\frac{10 \sqrt{3}}{3}$ ; BC = 20 $\sqrt{3}$

D. AB = $\frac{10 \sqrt{3}}{3}$ ; BC = $\frac{20 \sqrt{3}}{3}$

Xem đáp án

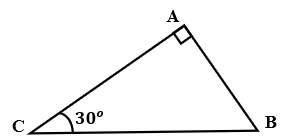
Xét tam giác ABC vuông tại A có:

Đáp án cần chọn là: D

Câu 6:

Cho tam giác ABC vuông tại A có AC = 20cm, $\hat{C} = 60^{0}$ . Tính AB, BC

A. AB = 20 $\sqrt{3}$ ; BC = 40

B. AB = 20 $\sqrt{3}$ ; BC = 40 $\sqrt{3}$

C. AB = 20; BC = 40

D. AB = 20; BC = 20 $\sqrt{3}$

Xem đáp án

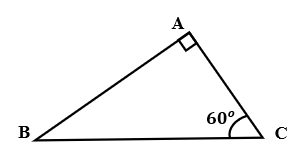
Xét tam giác ABC vuông tại A có:

Đáp án cần chọn là: A

Câu 7:

Cho tam giác ABC vuông tại A có BC = 12cm, $\hat{B} = 40^{0}$ . Tính AC; $\hat{C}$ (làm tròn đến chữ số thập phân thứ hai)

A. $A C \approx 7, 71; \hat{C} = 40^{0}$

B. $A C \approx 7, 72; \hat{C} = 50^{0}$

C. $A C \approx 7, 71; \hat{C} = 50^{0}$

D. $A C \approx 7, 73; \hat{C} = 50^{0}$

Xem đáp án

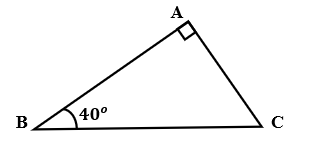
Xét tam giác ABC vuông tại A có:

Đáp án cần chọn là: C

Câu 8:

Cho tam giác ABC vuông tại A có BC = 15cm, $\hat{B} = 55^{0}$ . Tính AC; $\hat{C}$ (làm tròn đến chữ số thập phân thứ hai)

A. $A C \approx 12, 29; \hat{C} = 45^{0}$

B. $A C \approx 12, 29; \hat{C} = 35^{0}$

C. $A C \approx 12, 2; \hat{C} = 35^{0}$

D. $A C \approx 12, 92; \hat{C} = 40^{0}$

Xem đáp án

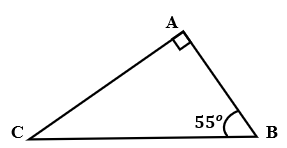
Xét tam giác ABC vuông tại A có:

Đáp án cần chọn là: B

Câu 9:

Cho tam giác ABC vuông tại A có BC = 15cm, AB = 12cm. Tính AC, $\hat{B}$

A. AC = 8 (cm); $\hat{B} \approx 36^{0} 52'$

B. AC = 9 (cm); $\hat{B} \approx 36^{0} 52'$

C. AC = 9 (cm); $\hat{B} \approx 37^{0} 52'$

D. AC = 9 (cm); $\hat{B} \approx 36^{0} 55'$

Xem đáp án

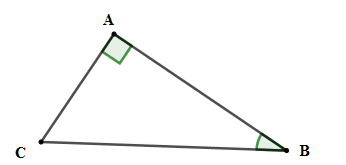
Xét tam giác ABC vuông tại A có:

Đáp án cần chọn là: B

Câu 10:

Cho tam giác ABC vuông tại A có AC = 7cm, AB = 5cm. Tính BC; $\hat{C}$

A. $B C = \sqrt{74} (c m); \hat{C} \approx 35^{0} 32'$

B. $B C = \sqrt{74} (c m); \hat{C} \approx 36^{0} 32'$

C. $B C = \sqrt{74} (c m); \hat{C} \approx 35^{0} 33'$

D. $B C = \sqrt{74} (c m); \hat{B} \approx 35^{0} 32'$

Xem đáp án

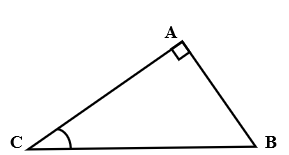
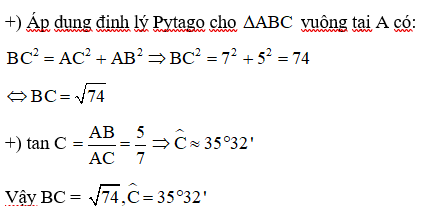
Đáp án cần chọn là: A

Câu 11:

Cho tam giác ABC vuông tại A có BC = 26cm, AB = 10cm. Tính AC, $\hat{B}$ (làm tròn đến độ)

A. AC = 22; $\hat{B} \approx 67^{0}$

B. AC = 24; $\hat{B} \approx 66^{0}$

C. AC = 24; $\hat{B} \approx 67^{0}$

D. AC = 24; $\hat{B} \approx 68^{0}$

Xem đáp án

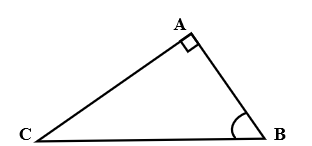
Xét tam giác ABC vuông tại A có:

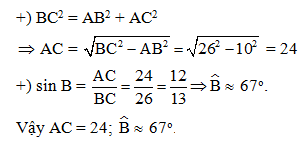
Đáp án cần chọn là: C

Câu 12:

Cho tam giác ABC có AB = 16, AC = 14 và $\hat{B} = 60^{0}$ . Tính BC

A. BC = 10

B. BC = 11

C. BC = 9

D. BC = 12

Xem đáp án

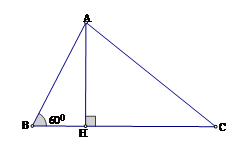
Kẻ đường cao AH

Xét tam giác vuông ABH, ta có:

Áp dụng định lý Py-ta-go vào tam giác vuông AHC ta có:

Suy ra HC = 2.

Vậy BC = CH + HB = 2 + 8 = 10

Đáp án cần chọn là: A

Câu 13:

Cho tam giác ABC có AB = 12, AC = 15 và $\hat{B} = 60^{0}$ . Tính BC

A. BC = $3 \sqrt{3} + 6$

B. BC = $3 \sqrt{13} + 6$

C. BC = 9

D. BC = 6

Xem đáp án

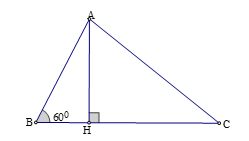
Kẻ đường cao AH

Xét tam giác vuông ABH, ta có:

Áp dụng định lý Py-ta-go vào tam giác vuông AHC ta có:

Đáp án cần chọn là: B

Câu 14:

Cho tam giác ABC có $\hat{B} = 60^{0}$ , $\hat{C} = 50^{0}$ , AC = 3,5cm. Diện tích tam giác ABC gần nhất với giá trị nào dưới đây?

A. 4

B. 5

C. 7

D.8

Xem đáp án

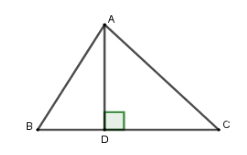
Kẻ đường cao AD

Xét tam giác vuông ACD, có:

Xét tam giác vuông ABD có:

Suy ra BC = BD + CD = 3,8

Đáp án cần chọn là: B

Câu 15:

Cho tam giác ABC có $\hat{B} = 70^{0}$ , $\hat{C} = 35^{0}$ , AC = 4,5cm. Diện tích tam giác ABC gần nhất với giá trị nào dưới đây? (làm tròn đến chữ số thập phân thứ hai)

A. 4

B. 5

C. 6

D. 8

Xem đáp án

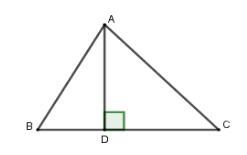
Kẻ đường cao AD

Xét tam giác vuông ACD, có:

Xét tam giác vuông ABD, có:

Suy ra BC = BD + DC = 0,94 + 3,69 = 4,63

Đáp án cần chọn là: C

Câu 16:

Tứ giác ABCD có $\hat{A} = \hat{D} = 90^{0}$ , $\hat{C} = 40^{0}$ , AB = 4cm, AD = 3cm. Tính diện tích tứ giác ABCD (làm tròn đến chữ số thập phân thứ hai).

A. 17,36 $c m^{2}$

B. 17,4 $c m^{2}$

C. 17,58 $c m^{2}$

D. 17,54 $c m^{2}$ .

Xem đáp án

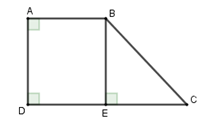
hay ABCD là hình thang vuông tại A, D

Kẻ BE $⊥$ DC tại E

Tứ giác ABED có ba góc vuông $\hat{A} = \hat{D} = 90^{0}$ nên ABED là hình chữ nhật

Suy ra DE = AB = 4cm; BE = AD = 3cm

Xét tam giác BEC vuông tại E có:

Do đó S_ABCD = $\frac{(A B + C D) . A D}{2}$ = $\frac{(4 + 4 + 3. \cot 40^{o}) .3}{2}$ $\approx 17, 36 c m^{2}$

Đáp án cần chọn là: A

Câu 17:

Tứ giác ABCD có $\hat{A} = \hat{D} = 90^{0}$ , $\hat{C} = 45^{0}$ , AB = 6cm, AD = 8cm. Tính diện tích tứ giác ABCD

A. 60 $c m^{2}$ .

B. 80 $c m^{2}$ .

C. 40 $c m^{2}$ .

D. 160 $c m^{2}$ .

Xem đáp án

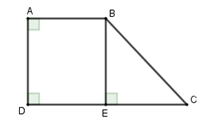
Vì $\hat{A} = \hat{D} = 90^{0}$ => AD // BC hay ABCD là hình thang vuông tại A, D

Kẻ BE $⊥$ DC tại E

Tứ giác ABED có ba góc vuông $\hat{A} = \hat{D} = \hat{E} = 90^{o}$ nên ABED là hình chữ nhật

Suy ra DE = AB = 6cm; BE = AD = 8cm

Xét tam giác BEC vuông tại E có $\hat{B C E} = 45^{0}$ nên tam giác BEC vuông cân tại E

EC = BE = 8cm

DC = DE + EC = 6 + 8 = 14cm

Do đó:

S_ABCD = $\frac{(A B + C D) . A D}{2}$ = $\frac{(6 + 14) 8}{2}$ = 80 $c m^{2}$ .

Đáp án cần chọn là: B

Câu 18:

Cho tam giác ABC cân tại A, $\hat{B} = 65^{0}$ , đường cao CH = 3,6. Hãy giải tam giác ABC

A. $\hat{A} = 50^{0}$ ; $\hat{C} = 65^{0}$ ; AB = AC = 5,6; BC = 8,52

B. $\hat{A} = 50^{0}$ ; $\hat{C} = 65^{0}$ ; AB = AC = 5,6; BC = 4,42

C. $\hat{A} = 50^{0}$ ; $\hat{C} = 65^{0}$ ; AB = AC = 4,7; BC = 4,24

D. $\hat{A} = 50^{0}$ ; $\hat{C} = 65^{0}$ ; AB = AC = 4,7; BC = 3,97

Xem đáp án

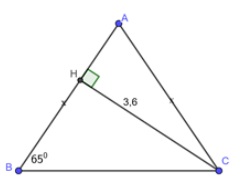
Vì ABC là tam giác cân tại A $\Rightarrow \hat{C} = \hat{B} = 65^{0}$

Ta có $\hat{A} + \hat{B} + \hat{C} = 180^{0}$ (định lý tổng ba góc trong một tam giác)

$\Rightarrow \hat{A} = 180^{0} - 2 \hat{C} = 180^{0} - 2 . 65^{0} = 50^{0}$

Xét ACH vuông tại H ta có:

Vì ABC là tam giác cân tại A $\Rightarrow A C = A B \approx 4, 7$

Xét BCH vuông tại H ta có:

Đáp án cần chọn là: D

Câu 19:

Cho tam giác ABC vuông tại A, đường cao AH, biết HB = 9; HC = 16. Tính góc B và góc C.

A. $\hat{B} = 53^{0} 8'$ ; $\hat{C} = 36^{0} 52'$

B. $\hat{B} = 36^{0} 52'$ ; $\hat{C} = 53^{0} 8'$

C. $\hat{B} = 48^{0} 35'$ ; $\hat{C} = 41^{0} 25'$

D. $\hat{B} = 41^{0} 25'$ ; $\hat{C} = 48^{0} 35'$

Xem đáp án

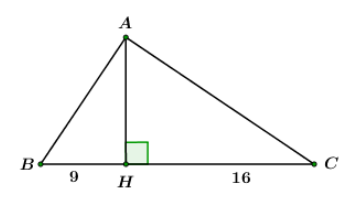
Ta có: BC = BH + CH = 9 + 16 = 25

Áp dụng hệ thức lượng cho ABC vuông tại A có đường cao AH ta có:

Xét ABC vuông tại A ta có:

Đáp án cần chọn là: A

Câu 20:

Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.

A. $\hat{A} = 45^{0}$ ; $\hat{B} = \hat{C} = 67^{0} 30'$

B. $\hat{A} = 30^{0}$ ; $\hat{B} = \hat{C} = 75^{0}$

C. $\hat{A} = 48^{0} 6'$ ; $\hat{B} = \hat{C} = 65^{0} 57'$

D. $\hat{A} = 53^{0} 8'$ ; $\hat{B} = \hat{C} = 63^{0} 26'$

Xem đáp án

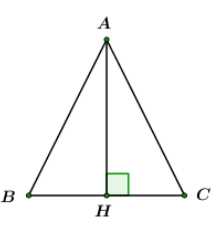
Giả sử BC = AH = a

Vì $Δ$ ABC là tam giác cân nên AH là đường cao đồng thời là đường trung tuyến

=> H là trung điểm BC => HB = HC = $\frac{B C}{2} = \frac{a}{2}$

Xét ABH vuông tại H ta có:

Vì ABC là tam giác cân

Ta có $\hat{A} = \hat{B} = \hat{C} = 180^{0}$ (định lý tổng ba góc trong một tam giác)

Đáp án cần chọn là: D

Câu 21:

Cho tam giác ABC vuông cân tại A (AB = AC = a). Phân giác của góc B cắt AC tại D. Tính DA; DC theo a

A. $A D = a . \cos 22, 5^{0}$ ; $D C = a - a . \cos 22, 5^{0}$ .

B. $A D = a . \sin 22, 5^{0}$ ; $D C = a - a . \sin 22, 5^{0}$ .

C. $A D = a . \tan 22, 5^{0}$ ; $D C = a - a . \tan 22, 5^{0}$ .

D. $A D = a . co t 22, 5^{0}$ ; $D C = a - a . c o t 22, 5^{0}$ .

Xem đáp án

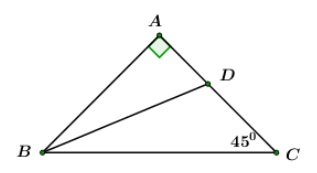
Vì tam giác ABC vuông cân tại

Vì BD là tia phân giác góc B

Xét $∆$ ABD vuông tại A ta có:

Đáp án cần chọn là: C

Câu 22:

Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC). Biết $\hat{A C B} = 60^{0}$ , CH = a. Tính độ dài AB và AC theo a

A. $\{\begin{cases} A B = 2 \sqrt{3} a \\ A C = 2 a \end{cases}$

B. $\{\begin{cases} A B = \sqrt{3} a \\ A C = \frac{1}{2} a \end{cases}$

C. $\{\begin{cases} A B = a \\ A C = 3 a \end{cases}$

D. $\{\begin{cases} A B = \sqrt{3} a \\ A C = a \end{cases}$

Xem đáp án

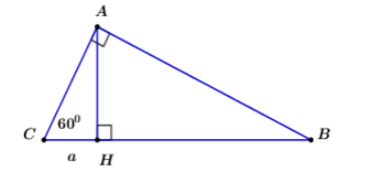
$∆$ ACH vuông tại H có:

Đáp án cần chọn là: A

Câu 23:

Cho hình thang ABCD vuông tại A và D; $\hat{C} = 50^{0}$ . Biết AB = 2; AD = 1,2. Tính diện tích hình thang ABCD

A. $S_{A B C D}$ = 2 (đvdt)

B. $S_{A B C D}$ = 3 (đvdt)

C. $S_{A B C D}$ = 4 (đvdt)

D. $S_{A B C D}$ = $\frac{5}{2}$ (đvdt)

Xem đáp án

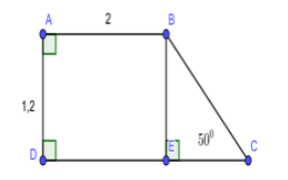
Đáp án cần chọn là: B

Câu 24:

Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính độ dài đường cao AH, tính $c o s \hat{A C B}$ và chu vi tam giác ABH.

A. AH = 2,8 cm; $c o s \hat{A C B} = \frac{3}{5}$

B. AH = 2,4 cm; $c o s \hat{A C B} = \frac{4}{5}$

C. AH = 2,5 cm; $c o s \hat{A C B} = \frac{3}{4}$

D. AH = 1,8 cm; $c o s \hat{A C B} = \frac{2}{3}$

Xem đáp án

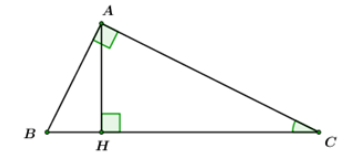
Áp dụng định lý Pytago trong $∆$ ABC vuông tại A ta có:

Áp dụng hệ thức lượng trong $∆$ ABC vuông tại A có đường cao AH ta có:

Đáp án cần chọn là: B

Câu 25:

Cho tam giác ABC vuông tại A; BC = a không đổi, $\hat{C} = α$ $(0^{0} < α < 90^{0})$

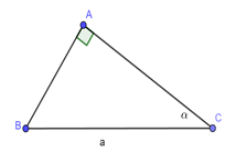
Lập công thức để tính diện tích tam giác ABC theo a và

A. $\frac{1}{2} a^{2} \sin α . \cos α$

B. $a^{2} \sin α . \cos α$

C. $2 a^{2} \sin α . \cos α$

D. $3 a^{2} \sin α . \cos α$

Xem đáp án

Xét $∆$ ABC vuông tại A ta có: $\{\begin{cases} A B = B C . \sin α = a . \sin α \\ A C = B C . \cos α = a . c o s α \end{cases}$

Đáp án cần chọn là: A

Câu 26:

Cho tam giác ABC vuông tại A; BC = a không đổi, $\hat{C} = α$ $(0^{0} < α < 90^{0})$

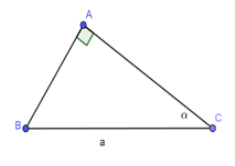
Tìm góc để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy.

A. $α = 45^{0}$ ; $m a x_{S_{A B C}} = \frac{1}{2} a^{2}$ .

B. $α = 30^{0}$ ; $m a x_{S_{A B C}} = \frac{\sqrt{3}}{4} a^{2}$ .

C. $α = 60^{0}$ ; $m a x_{S_{A B C}} = \frac{\sqrt{3}}{4} a^{2}$ .

D. $α = 45^{0}$ ; $m a x_{S_{A B C}} = \frac{1}{4} a^{2}$ .

Xem đáp án

$S_{A B C}$ = $\frac{1}{2}$ . AB. AC $\leq \frac{1}{2} . \frac{(A B^{2} + A C^{2})}{2} = \frac{1}{4} . (A B^{2} + A C^{2})$

Áp dụng định lý Py-ta-go cho ABC vuông tại A ta có:

Dấu “=” xảy ra AC = AB => $∆$ ABC vuông cân

Đáp án cần chọn là: D

Câu 27:

Cho tam giác DEF có DE = 7cm; $\hat{D} = 40^{0}$ ; $\hat{F} = 58^{0}$ . Kẻ đường cao EI của tam giác đó.

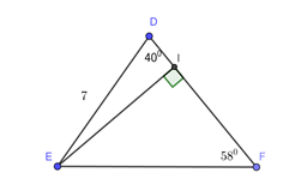
Hãy tính: (Kết quả làm tròn đến chữ số thập phân thứ 1). Đường cao EI:

A. EI = 4,5cm

B. EI = 5,4cm

C. EI = 5,9cm

D. EI = 5,6cm

Xem đáp án

Xét $∆$ DEI vuông tại I ta có:

Đáp án cần chọn là: A

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 9 Bài 4 (có đáp án): Một số hệ thức về cạnh và góc trong tam giác vuông (phần 2)

Trắc nghiệm Toán 9 Bài 4 (có đáp án): Một số hệ thức về cạnh và góc trong tam giác vuông (phần 2)

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương