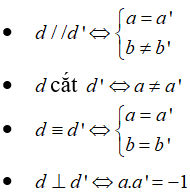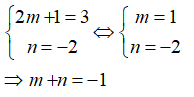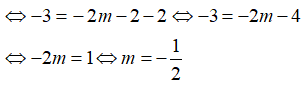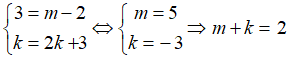21 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 9 Bài 4 (có đáp án): Đường thẳng song song và đường thẳng cắt nhau

Câu 1:

Hai đường thẳng d: y = ax + b (a $\neq$ 0) và d': y = a'x + b'(a' $\neq$ 0) cắt nhau khi:

A. a $\neq$ a'

B. $\{\begin{cases} a \neq a' \\ b \neq b' \end{cases}$

C. $\{\begin{cases} a = a' \\ b \neq b' \end{cases}$

D. $\{\begin{cases} a \neq a' \\ b = b' \end{cases}$

Xem đáp án

Đáp án A

Cho hai đường thẳng d: y = ax + b (a $\neq$ 0) và d': y = a'x + b'(a' $\neq$ 0)

d cắt d' ⇔ a $\neq$ a'

Câu 2:

Hai đường thẳng d: y = ax + b(a $\neq$ 0) và d': y = a'x + b'(a' $\neq$ 0) có a = a' và b $\neq$ b' . Khi đó:

A. d // d'

B. d $\equiv$ d'

C. d cắt d'

D. d $⊥$ d'

Xem đáp án

Đáp án A

Cho hai đường thẳng d: y = ax + b(a $\neq$ 0) và d': y = a'x + b'(a' $\neq$ 0)

Câu 3:

Cho hai đường thẳng d: y = x + 3 và d': y = -2x . Khi đó:

A. d // d'

B. d $\equiv$ d'

C. d cắt d'

D. d $⊥$ d'

Xem đáp án

Đáp án C

Ta thấy d: y = x + 3 có a = 1 và d': y = -2x có a' = -2 ⇒ a $\neq$ a' (1 $\neq$ -2) nên d cắt d'

Câu 4:

Cho hai đồ thị của hàm số bậc nhất là hai đường thẳng d: y = (m + 2)x - m và d': y = -2x - 2m + 1. Với giá trị nào của m thì d cắt d' ?

A. m $\neq$ -2

B. m $\neq$ -4

C. m $\neq$ -2; m $\neq$ -4

D. m $\neq$ 2; m $\neq$ 4

Xem đáp án

Đáp án C

• Ta thấy d: y = (m + 2)x - m có a = m + 2 và d': y = -2x - 2m + 1 có a' = -2

• Để y = (m + 2)x - m là hàm số bậc nhất thì m + 2 $\neq$ 0 ⇔ m $\neq$ -2

• Để d cắt d' ⇔ a $\neq$ a' ⇔ m + 2 $\neq$ -2 ⇔ m $\neq$ -4

Vậy m $\neq$ -2; m $\neq$ -4

Câu 5:

Cho hai đồ thị của hàm số bậc nhất là hai đường thẳng d: y = (m + 2)x - m và d': y = -2x - 2m + 1. Với giá trị nào của m thì d // d' ?

A. m = -2

B. m = -4

C. m = 2

D. m $\neq$ 2; m $\neq$ -4

Xem đáp án

Đáp án B

• Ta thấy d: y = (m + 2)x - m có a = m + 2; b = -m và d': y = -2x - 2m + 1 có

• Để y = (m + 2)x - m là hàm số bậc nhất thì m + 2 $\neq$ 0 ⇔ m $\neq$ -2

• Để d // d' ⇔ a = a'; b ≠ b'

a = a' ⇔ m + 2 = -2 ⇔ m = -4

b $\neq$ b' ⇔ -m $\neq$ -2m + 1 ⇔ m $\neq$ 1

Vì m = -4 thỏa mãn m $\neq$ -2; m $\neq$ 1 nên giá trị m cần tìm là m = -4

Vậy m = -4

Câu 6:

Cho hàm số y = (2m + 1) x + n . Biết rằng đồ thị hàm số trùng với đường thẳng y = 3x - 2. Tính m + n?

A. -1

B. 0

C. 1

D. 2

Xem đáp án

Đáp án A

Để đồ thị hàm số y = (2m + 1)x + n trùng với đường thẳng y = 3x - 2 thì:

Câu 7:

Cho hàm số bậc nhất y = (2m + 1)x + 3.Tìm m để đồ thị hàm số cắt đường thẳng y = x + 1 tại điểm có tung độ bằng 2?

A. m = 1

B. m = 0

C. m = -1

D. m = 2

Xem đáp án

Đáp án C

Điều kiện để hàm số đã cho là hàm số bậc nhất là: 2m + 1 $\neq$ 0 ⇔ m $\neq$ $\frac{- 1}{2}$

* Ta tìm tọa độ điểm A thuộc đường thẳng y= x + 1 có tung độ bằng 2:

⇒ 2 = x + 1 ⇔ x = 1 ⇒ A(1; 2)

* vì đồ thị hàm số y = (2m + 1)x + 3 cắt đường thẳng y = x + 1 tại điểm có tung độ bằng 2 nên đồ thị hàm số y = (2m + 1)x + 3 đi qua A(1;2).

⇒ 2 = (2m + 1).1 + 3 ⇔ 2 = 2m + 4

⇔ -2m = 2 ⇔ m = -1 (tm)

Câu 8:

Cho ba đường thẳng $d_{1}$ : y = 2x +1; $d_{2}$ : y = x – 1 và $d_{3}$ : y = (m + 1)x – 2. Tìm m để ba đường thẳng đã cho đồng quy.

A. m = -1

B. $m = \frac{1}{2}$

C. $m = \frac{- 1}{2}$

D. $m = - \frac{1}{4}$

Xem đáp án

Đáp án C

Hoành độ giao điểm của $d_{1}$ và $d_{2}$ là nghiệm phương trình:

2x + 1 = x -1 nên x = -2

Với x = -2 thì y = 2. (-2) + 1 = -3

Vậy 2 đường thẳng $d_{1}$ và d2 cắt nhau tại A(-2; -3).

Để ba đường thẳng đã cho đồng quy thì điểm A(-2; -3) thuộc đồ thị hàm số y = (m + 1)x – 2

Suy ra: -3 = (m + 1).(-2) - 2

Câu 9:

Cho đồ thị hàm số y = (m -2)x + 8. Tìm m biết rằng đồ thị hàm số cắt trục hoành tại tại điểm có hoành độ là 2?

A. m = -2

B. m = 2

C. m = 1

D. m = -1

Xem đáp án

Đáp án A

Vì đồ thị hàm số cắt trục hoành tại tại điểm có hoành độ là 2 nên điểm A(2; 0) thuộc đồ thị hàm số đã cho.

Thay x = 2; y = 0 ta được: 0 = (m -2).2 + 8

⇔ 0 = 2m - 4 + 8 ⇔ 0 = 2m + 4 ⇔ m = -2

Câu 10:

Cho hai hàm số y = 3x + k và y = (m -2)x + (2k + 3). Biết rằng đồ thị hai hàm số đã cho trùng nhau. Tính m + k ?

A. 1

B. -2

C.3

D. 2

Xem đáp án

Đáp án D

Vì đồ thị hai hàm số đã cho trùng nhau nên:

Câu 11:

Viết phương trình đường thẳng d biết d song song với đường thẳng $y = - 5 x - 3$ và cắt trục hoành tại điểm có hoành độ bằng 5

A. $y = \frac{1}{5} x - 25$

B. $y = 5 x + 25$

C. $y = - 5 x + 25$

D. $y = - 5 x - 25$

Xem đáp án

Gọi phương trình đường thẳng d cần tìm là $y = a x + b (a \neq 0)$

Vì d song song với đường thẳng $y = - 5 x - 3 n ê n a = - 5; b \neq - 3 \Rightarrow d : y = - 5 x + b$

Giao điểm của đường thẳng d với trục hoành có tọa độ (5; 0)

Thay $x = 5; y = 0$ vào phương trình đường thẳng d: $y = - 5 x + b$ ta được

$- 5 . 5 + b = 0 \Rightarrow b = 25 (T M) \Rightarrow y = - 5 x + 25$

Vậy d: $y = - 5 x + 25$

Đáp án cần chọn là: C

Câu 12:

Viết phương trình đường thẳng d biết d đi qua hai điểm A (1; 2); B (−2; 0)

A. $y = - \frac{2}{3} x - \frac{4}{3}$

B. $y = - \frac{2}{3} x + \frac{4}{3}$

C. $y = \frac{2}{3} x - \frac{4}{3}$

D. $y = \frac{2}{3} x + \frac{4}{3}$

Xem đáp án

Gọi phương trình đường thẳng d cần tìm là $y = a x + b (a \neq 0)$

Thay tọa độ điểm A vào phương trình đường thẳng d ta được $a + b = 2 \Rightarrow b = 2 - a$

Thay tọa độ điểm B vào phương trình đường thẳng d ta được $- 2 a + b = 0 \Rightarrow b = 2 a$

Suy ra $2 a = 2 - a \Leftrightarrow a = \frac{2}{3} \Rightarrow b = 2. \frac{2}{3} = \frac{4}{3} \Rightarrow y = \frac{2}{3} x + \frac{4}{3} (T M)$

Vậy d: $y = \frac{2}{3} x + \frac{4}{3}$

Đáp án cần chọn là: D

Câu 13:

Viết phương trình đường thẳng d biết d đi qua hai điểm A (3; 3); B (−1; 4)

A. $y = \frac{1}{4} x - \frac{15}{4}$

B. $y = - \frac{1}{4} x + \frac{15}{4}$

C. $y = - \frac{1}{4} x - \frac{15}{4}$

D. $y = \frac{1}{4} x + \frac{15}{4}$

Xem đáp án

Gọi phương trình đường thẳng d cần tìm là $y = a x + b (a \neq 0)$

Thay tọa độ điểm A vào phương trình đường thẳng d ta được $3 a + b = 3 \Rightarrow b = 3 - 3 a$

Thay tọa độ điểm B vào phương trình đường thẳng d ta được $- 1 . a + b = 4 \Rightarrow b = 4 + a$

Suy ra $3 - 3 a = 4 + a \Leftrightarrow 4 a = - 1 \Leftrightarrow a = - \frac{1}{4} \Rightarrow b = 4 + a = 4 + (- \frac{1}{4})$

$\Rightarrow b = \frac{15}{4} \Rightarrow y = \frac{- 1}{4} x + \frac{15}{4}$

Vậy d: $y = - \frac{1}{4} x + \frac{15}{4}$

Đáp án cần chọn là: B

Câu 14:

Tìm điểm cố định mà đường thẳng d: $y = 3 m x - (m + 3)$ đi qua với mọi m.

A. $M (\frac{1}{3}; 3)$

B. $M (\frac{1}{3}; - 3)$

C. $M (- \frac{1}{3}; - 3)$

D. $M (- \frac{1}{3}; 3)$

Xem đáp án

Gọi M (x; y) là điểm cố định cần tìm khi đó

$3 m x - (m + 3) = y$ đúng với mọi m

$3 m x - m - 3 - y = 0$ đúng với mọi m

$m (3 x - 1) + - 3 - y = 0$ đúng với mọi m

$\Leftrightarrow \{\begin{cases} 3 x - 1 = 0 \\ - 3 - y = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{1}{3} \\ y = - 3 \end{cases} \Rightarrow M (\frac{1}{3}; - 3)$

Vậy điểm $M (\frac{1}{3}; - 3)$ là điểm cố định cần tìm.

Đáp án cần chọn là: B

Câu 15:

Tìm điểm cố định mà đường thẳng d: $y = (5 - 2 m) x + m + 1$ đi qua với mọi m

A. $M (\frac{7}{2}; \frac{1}{2})$

B. M (1; 7)

C. $M (- \frac{1}{2}; \frac{7}{2})$

D. $M (\frac{1}{2}; \frac{7}{2})$

Xem đáp án

Gọi M (x; y) là điểm cố định cần tìm, khi đó

$(5 - 2 m) x + m + 1 = y$ đúng với mọi m

$- 2 m x + m + 1 + 5 x - y = 0$ đúng với mọi m

$m (- 2 x + 1) + 1 - y + 5 x = 0$ đúng với mọi m

$\begin{array}{l} \Leftrightarrow \{\begin{cases} - 2 x + 1 = 0 \\ 1 - y + 5 x = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{1}{2} \\ 1 - y + 5. \frac{1}{2} = 0 \end{cases} \\ \Leftrightarrow \{\begin{cases} x = \frac{1}{2} \\ y = \frac{7}{2} \end{cases} \Rightarrow M (\frac{1}{2}; \frac{7}{2}) \end{array}$

Vậy điểm $M (\frac{1}{2}; \frac{7}{2})$ là điểm cố định cần tìm

Đáp án cần chọn là: D

Câu 16:

Cho đường thẳng d: $y = (m^{2} - 2 m + 2) x + 4$ . Tìm m để d cắt Ox tại A và cắt Oy tại B sao cho diện tích tam giác OAB lớn nhất.

A. $m = 1$

B. $m = 0$

C. $m = - 1$

D. $m = 2$

Xem đáp án

$\begin{array}{l} d \cap O y = \{B\} \\ x_{B} = 0 \Rightarrow y_{B} = 4 \Leftrightarrow B (0; 4) \Rightarrow O B = |4| = 4 \\ d \cap O x = \{A\} \\ y_{A} = 0 \Leftrightarrow (m^{2} - 2 m + 2) x_{A} + 4 = 0 \\ x_{A} = \begin{array}{l} x_{A} = \frac{- 4}{m^{2} - 2 m + 2} \Rightarrow A (\frac{- 4}{m^{2} - 2 m + 2}; 0) \\ \Rightarrow O A |\frac{- 4}{m^{2} - 2 m + 2}| \end{array} \end{array}$

$\ S_{Δ A O B} = \frac{1}{2} O A . O B = \frac{1}{2} .4. |\frac{- 4}{m^{2} - 2 m + 2}| = \frac{8}{{(m - 1)}^{2} + 1}$

Ta có ${(m - 1)}^{2} + 1 \geq 1 \forall m$

Do đó $S_{Δ A O B} = \frac{8}{{(m - 1)}^{2} + 1} \leq \frac{8}{1} = 8$

Dấu “=” xảy ra khi $m - 1 = 0 \Leftrightarrow m = 1$

Hay tam giác OAB có diện tích lớn nhất là 8 khi $m = 1$

Đáp án cần chọn là: A

Câu 17:

Điểm cố định mà đường thẳng d: $y = \frac{\sqrt{k} + 1}{\sqrt{3} - 1} x + \sqrt{k} + 3 (k \geq 0)$ luôn đi qua là:

A. $M (1 - \sqrt{3}; \sqrt{3} - 1)$

B. $M (\sqrt{3}; \sqrt{3})$

C. $M (\sqrt{3}; \sqrt{3} - 1)$

D. Cả A, B, C đều sai

Xem đáp án

Gọi M $(x_{0}; y_{0})$ là điểm cố định mà d luôn đi qua.

$M (x 0; y 0) \in d \forall k$

$\Leftrightarrow y_{0} = \frac{\sqrt{k} + 1}{\sqrt{3} - 1} x_{0} + \sqrt{k} + \sqrt{3} \forall k \Leftrightarrow \sqrt{k} x_{0} + x_{0} + \sqrt{3 k} - \sqrt{k} - \sqrt{3} + 3 - \sqrt{3} y_{0} + y_{0} = 0 \forall k \Leftrightarrow \sqrt{k} (x_{0} + \sqrt{3} - 1) + x_{0} + 3 - \sqrt{3} + (1 - \sqrt{3}) y_{0} = 0 \forall k \begin{array}{l} \Leftrightarrow \{\begin{cases} x_{0} + \sqrt{3} - 1 = 0 \\ x_{0} + (1 - \sqrt{3}) y_{0} + 3 - \sqrt{3} = 0 \end{cases} \\ \Leftrightarrow \{\begin{cases} x_{0} = 1 - \sqrt{3} \\ (1 - \sqrt{3}) + (1 - \sqrt{3}) y_{0} + 3 - \sqrt{3} = 0 \end{cases} \end{array} \begin{array}{l} \Leftrightarrow \{\begin{cases} x_{0} = 1 - \sqrt{3} \\ (1 - \sqrt{3}) y_{0} + 4 - 2 \sqrt{3} = 0 \end{cases} \\ \Leftrightarrow \{\begin{cases} x_{0} = 1 - \sqrt{3} \\ (1 - \sqrt{3}) y_{0} + {(1 - \sqrt{3})}^{2} = 0 \end{cases} \\ \Leftrightarrow \{\begin{cases} x_{0} = 1 - \sqrt{3} \\ y_{0} = - 1 + \sqrt{3} \end{cases} \end{array} \Rightarrow M (1 - \sqrt{3}; \sqrt{3} - 1)$

là điểm cố định mà d luôn đi qua

Đáp án cần chọn là: A

Câu 18:

Cho đường thẳng $d : y = (2 m + 1) x - 1$ . Tìm m để đường thẳng d cắt hai trục tọa độ tạo thành tam giác có diện tích bằng $\frac{1}{2}$

A. $m = 0$

B. $m = 1$

C. $m = - 1$

D. Cả A và C đều đúng

Xem đáp án

$d \cap O y = \{B\} \Rightarrow x_{B} = 0 \Rightarrow y_{B} = - 1 \Rightarrow B (0; - 1) \Rightarrow O B = |- 1| = 1 d \cap O x = \{A\} \Rightarrow y_{A} = 0 \Leftrightarrow (2 m + 1) {.x}_{A} - 1 = 0 \Leftrightarrow x_{A} = \frac{1}{2 m + 1} (m \neq \frac{- 1}{2})$

$\Rightarrow A (\frac{1}{2 m + 1}; 0) \Rightarrow O A = |\frac{1}{2 m + 1}|$

$\begin{array}{l} S_{Δ A O B} = \frac{1}{2} O A . O B = \frac{1}{2} .1. |\frac{1}{2 m + 1}| = \frac{1}{2} \\ \Leftrightarrow | 2 m + 1 | = 1 \Leftrightarrow [\begin{array}{l} m = 0 \\ m = - 1 \end{array} \end{array}$

Đáp án cần chọn là: D

Câu 19:

Biết đường thẳng d: $y = m x + 4$ cắt Ox tại A và cắt Oy tại B sao cho diện tích tam giác OAB bằng 6. Khi đó giá trị của m là:

A. $m = \pm \frac{4}{3}$

B. $m < \frac{4}{3}$

C. $m > \frac{4}{3}$

D. $m = \frac{4}{3}$

Xem đáp án

$d \cap O y = \{B\} ⇒ x_{B} = 0 \Rightarrow y_{B} = 4 \Rightarrow B (0; 4) \Rightarrow O B = |4| = 4 d \cap O x = \{A\} \Rightarrow y_{A} = 0 \Rightarrow m x_{A} + 4 = 0 \Leftrightarrow x_{A} = \frac{- 4}{m} (m \neq 0)$

$\Rightarrow A (\frac{- 4}{m}; 0) \Rightarrow O A = |\frac{4}{m}|$

$\begin{array}{l} S_{Δ A O B} = \frac{1}{2} O A . O B = \frac{1}{2} .4. |\frac{4}{m}| = 6 \\ \Leftrightarrow | m | = \frac{4}{3} \Leftrightarrow m = \pm \frac{4}{3} \end{array}$

Đáp án cần chọn là: A

Câu 20:

Cho đường thẳng d: $y = (k - 2) x - 1$ . Tìm k để d cắt 2 trục tọa độ tạo thành tam giác có diện tích bằng 1

A. $k = \frac{5}{2}$

B. $k = \frac{3}{2}$

C. $k = 1$

D. Cả A và B đều đúng

Xem đáp án

$d \cap O y = \{B\} ⇒ x_{B} = 0 \Rightarrow y_{B} = - 1 \Rightarrow B (0; - 1) \Rightarrow O B = |- 1| = 1 d \cap O x = \{A\} ⇒ y_{A} = 0 \Leftrightarrow (k - 2) x_{A} - 1 = 0 \Leftrightarrow x_{A} = \frac{1}{k - 2} (k \neq 2)$

$\Rightarrow A (\frac{1}{k - 2}; 0) \Rightarrow O A = |\frac{1}{k - 2}|$

$\begin{array}{l} S_{Δ A O B} = \frac{1}{2} O A . O B = 1 \Leftrightarrow \frac{1}{2} .1. |\frac{1}{k - 2}| = 1 \\ \Leftrightarrow | k - 2 | = \frac{1}{2} \Leftrightarrow [\begin{array}{l} k = \frac{5}{2} \\ k = \frac{3}{2} \end{array} \end{array}$ (tmdk)

Đáp án cần chọn là: D

Câu 21:

Cho đường thẳng d: $y = m x + m - 1$ . Tìm m để d cắt Ox tại A và cắt Oy tại B sao cho tam giác AOB vuông cân.

A. $m < 1$

B. $m = 1$

C. $m > 1$

D. $m = 1 h o ặ c m = - 1$

Xem đáp án

$d \cap O y = \{B\} ⇒ x_{B} = 0 \Rightarrow y_{B} = m - 1 \Rightarrow B (0; m - 1) \Rightarrow O B = |m - 1| d \cap O x = \{A\} \Rightarrow y_{A} = 0 \Rightarrow m x_{A} + m - 1 = 0 \Leftrightarrow x_{A} = \frac{1 - m}{m} (m \neq 0)$

$\Rightarrow A (\frac{1 - m}{m}; 0) \Rightarrow O A = |\frac{1 - m}{m}|$

Tam giác OAB vuông cân tại O

$O A = O B \Leftrightarrow |m - 1| = |\frac{1 - m}{m}| \Leftrightarrow [\begin{array}{l} m - 1 = \frac{1 - m}{m} \\ m - 1 = \frac{m - 1}{m} \end{array} \Leftrightarrow [\begin{array}{l} m^{2} = 1 \\ (m - 1) (1 - \frac{1}{m}) = 0 \end{array}$

$\Leftrightarrow [\begin{array}{l} m = \pm 1 \\ \frac{{(m - 1)}^{2}}{m} = 0 \end{array} \Leftrightarrow m = \pm 1$

Đáp án cần chọn là: D

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Toán 9 Bài 4 (có đáp án): Đường thẳng song song và đường thẳng cắt nhau

Trắc nghiệm Toán 9 Bài 4 (có đáp án): Đường thẳng song song và đường thẳng cắt nhau

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương