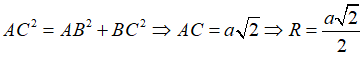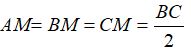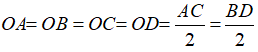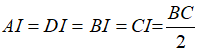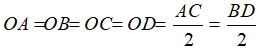Trắc nghiệm Toán 9 Bài 1 (có đáp án): Sự xác định đường tròn. Tính chất đối xứng của đường tròn.
Trắc nghiệm Toán 9 Bài 1 (có đáp án): Sự xác định đường tròn. Tính chất đối xứng của đường tròn.
-
1078 lượt thi
-
10 câu hỏi
-
15 phút
Danh sách câu hỏi
Câu 1:
Số tâm đối xứng của đường tròn là
Đáp án A
Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.
Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn
Câu 2:
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn
Đáp án D
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn
Nên đường tròn có vô số trục đối xứng
Câu 3:
Tâm của đường tròn ngoại tiếp tam giác là
Đáp án B
Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó
Câu 4:
Cho đường tròn (O; R) và điểm M bất kì, biết rằng OM = R . Chọn khẳng định đúng?
Đáp án B
Cho điểm M và đường tròn (O; R) ta so sánh khoảng cách OM với bán kính R để xác định vị trí tương đối theo bảng sau:
Câu 5:
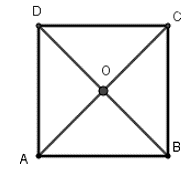
Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a
Đáp án C
Gọi O là giao hai đường chéo của hình vuông ABCD.
Khi đó theo tính chất của hình vuông ta có OA = OB = OC = OD nên O là tâm đường tròn ngoại tiếp hình vuông ABCD, bán kính R = OA = AC/2
Xét tam giác ABC vuông B tại ta có:
Vậy tâm đường tròn ngoại tiếp hình vuông ABCD cạnh a là giao điểm hai đường chéo, bán kính là
Câu 6:
Cho tam giác ABC vuông tại A. Khi đó, tâm đường tròn ngoại tiếp tam giác ABC là?
Đáp án D
Gọi M là trung điểm của BC.
Tam giác ABC vuông tại A có đường trung tuyến AM ứng với cạnh huyền BC nên:
Suy ra, điểm M là tâm đường tròn ngoại tiếp tam giác ABC
Câu 7:
Cho tứ giác ABCD là hình bình hành và . Tìm tâm đường tròn ngoại tiếp tứ giác ABCD?
Đáp án A
Vì tứ giác ABCD là hình bình hành và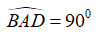 
nên ABCD là hình chữ nhật.
Gọi O là giao điểm hai đường chéo.
Theo tính chất hình chữ nhật ta có:
Do đó, O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
Câu 8:
Cho 4 điểm phân biệt A, B, C và D sao cho tam giác ABC vuông tại A và tam giác BCD vuông tại D. Tìm tâm đường tròn ngoại tiếp tứ giác ABCD?
Đáp án C
Gọi I là trung điểm BC.
Ta có; tam giác BCD vuông tại D có DI là đường trung tuyến ứng với cạnh huyền BC nên:
(1)
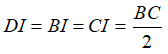
Tam giác ABC vuông tại A có AI là đường trung tuyến ứng với cạnh huyền BC nên:
(2)
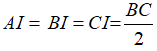
Từ (1) và (2) suy ra: 
Do đó, I là tâm đường tròn ngoại tiếp tứ giác ABCD.
Câu 9:
Cho hình thoi ABCD có AC = BD . Tìm tâm đường tròn ngoại tiếp hình thoi ABCD ?
Đáp án B
Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..
Gọi O là tâm hình vuông.
Theo tính chất hình vuông ta có:
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.
Câu 10:
Hình tròn tâm I, bán kính R = 4cm là gồm tất cả các điểm ........
Đáp án D
Hình tròn tâm I, bán kính R = 4cm là gồm tất cả các điểm có khoảng cách đến điểm I nhỏ hơn hoặc bằng 4 cm.
Chú ý tránh nhầm lẫn giữa khái niệm đường tròn và hình tròn.