Bài tập theo tuần Toán 9 - Tuần 16
-
349 lượt thi
-
13 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Vì nên hệ có nghiệm duy nhất
Câu 4:
Đoán nhận số nghiệm hệ phương trình sau, có giải thích
Vì nên hệ có nghiệm duy nhất
Câu 5:
Chứng tỏ rằng hệ phương trình có 1 nghiệm duy nhất với m = 3. Tìm nghiệm đó.
Khi hệ có nghiệm duy nhất
Câu 10:
Tọa độ giao điểm của là nghiệm hệ
Thay (2; 4) vào đều thỏa
Vậy 4 đường thẳng đồng quy tại (2; 4)
Câu 11:
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại S. Kẻ tiếp tuyến chung ngoài AB, CD với A, C thuộc (O),
Chứng minh rằng
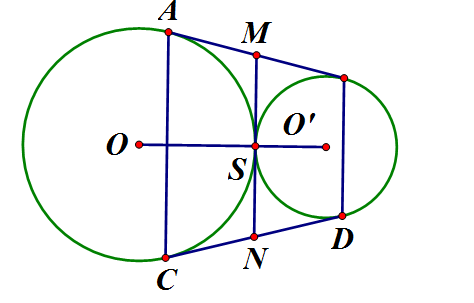
Vẽ tiếp tuyến chung tại S lần lượt cắt AB, CD ở M, N. Theo tính chất tiếp tuyến ta có:
do đó:
Mặt khác OO' là trục đối xứng của hình nên C đối xứng với A qua OO', D đối xứng với B qua OO' nên do đó là hình thang.
M, N lần lượt là trung điểm của AB, CD nên MN là đường trung bình hình thang ABCD.
Từ (1) và (2) suy ra
Câu 12:
Cho vuông tại A (AB < AC) nội tiếp đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng:
a) cân
b) cân
c) HA là tiếp tuyến của (O)
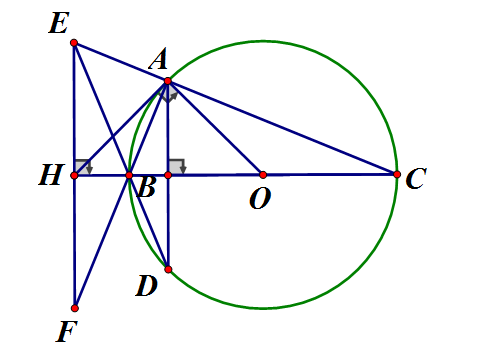
a) Vì AD // EF (cùng vuông góc BC) (so le trong ) (1)
Ta lại có có BO vừa là đường cao vừa là đường trung tuyến (tính chất tiếp tuyến – dây cung) nên cân tại mà (so le trong) (3)
Từ (1), (2), (3) cân tại B
b) cân tại B đường cao cũng là trung tuyến là trung điểm EF vuông tại A, AH đường trung tuyến
cân tại H
c) Vì cân tại H mà (cùng phụ góc E) (5)
cân ) (6)
Từ (4), (5), (6)
và là tiếp tuyến của (O).
Câu 13:
Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB, AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC
a) Chứng minh rằng: tứ giác BDCE là hình thoi
b) Gọi I là giao điểm của OC và đường tròn (O'). Chứng minh ba điểm D, A, I thẳng hàng
c) Chứng minh rằng KI là tiếp tuyến của đường tròn (O')
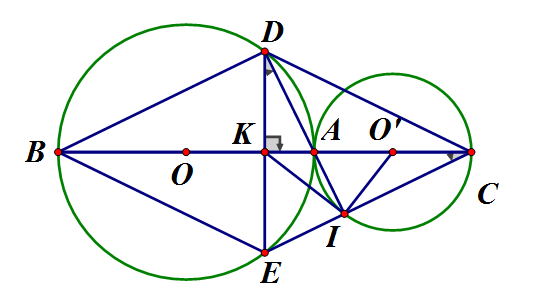
Ta có: tại K nên K là trung điểm Tứ giác BDCE có hai dường chéo BC, DE vuông góc nhau tại trung điểm mỗi đường
là hình thoi
Ta có: (so le trong ) (1)
là đường kính (2)
Từ (1), (2) suy ra và có:
mà hai góc ở vị trí đối đỉnh và B, K, C thẳng hàng nên D, A, I thẳng hàng
vuông tại I có IK trung tuyến
Mà (cùng phụ
Lại có ( cân tại O') (5)
Từ (3), (4), (5)
Và là tiếp tuyến của (O')
