5 câu hỏi trắc nghiệm thuộc Chủ đề 1: Định lí PYTHAGORE và những ứng dụng trong các bài toán thực tế có đáp án

Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 9: Bài toán thực tế Hình học có đáp án

Chủ đề 1: Định lí PYTHAGORE và những ứng dụng trong các bài toán thực tế có đáp án

1754 lượt thi
5 câu hỏi
60 phút

Danh sách câu hỏi

Câu 1:

Từ đỉnh một cái cây có treo một cái dây thả xuống đất thì thừa một đoạn có độ dài là $d$ . Nếu kéo căng dây ra thì đầu dây chạm đất ở một khoảng cách là $b$ so với gốc cây. Hãy tìm độ dài của dây.

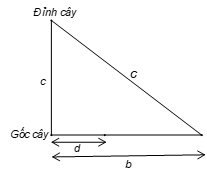
Từ đỉnh một cái cây có treo một cái dây thả xuống đất thì thừa một đoạn có độ dài là d. Nếu (ảnh 1)

Xem đáp án

Nếu cây có độ dài $a$ thì có bài toán là tính độ dài $c$ của cạnh huyền một tam giác vuông có cạnh bên là $a = c - d$ và $b$ . Theo định lí Pythagore ta có:

$a = c - d$ .

Từ đây suy ra: $c = \frac{b^{2} + d^{2}}{2 d}$ .

Câu 2:

Có một cây tre có độ cao là a. Khi gãy ngọn tre chạm đất ở một khoảng cách là b so với gốc tre. Hãy tìm độ cao chỗ cây tre.

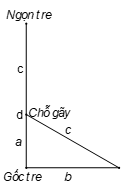
Có một cây tre có độ cao là a. Khi gãy ngọn tre chạm đất ở một khoảng cách là b so với gốc tre. (ảnh 1)

Xem đáp án

Ta phải tính cạnh a của một tam giác vuông có cạnh bên là b và cạnh huyền là $c = d - a$ .

Theo định lí Pythagore ta có: $a^{2} + b^{2} = {(d - a)}^{2}$ .

Từ đây suy ra: $a = \frac{d^{2} - b^{2}}{2 d}$ .

Câu 3:

Có một cái ao hình vuông, mỗi cạnh dài 3,33m, chính giữa cái ao có một cây sậy nhô lên khỏi mặt nước vừa đúng 0,33m, kéo ngọn cây sậy vào bờ thì chọn cây vừa chạm mặt nước. Hỏi độ sau của nước và cây sậy cao bao nhiêu?

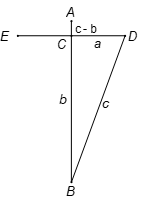
Có một cái ao hình vuông, mỗi cạnh dài 3,33m, chính giữa cái ao có một cây sậy nhô lên khỏi mặt (ảnh 1)

Xem đáp án

Giả sử chiều rộng của ao là $E D = 2 a = 3,33$ (m), C là trung điểm của ED nên: $D C = a = 1,665$ (m).

Chiều cao cây sậy mặt giữa ao là AB, phần nhô khỏi mặt nước $A C = 0,33$ (m).

Mà $A B = B D$ , giả sử $B D = c$ , độ sâu của nước $B C = b$ , tam giác BCD là tam giác vuông. Rõ ràng là $A C = A B - B C = c - b = 0,33$ (m).

Độ dài của AC bằng hiệu giữa đường huyền với cạnh dài của góc vuông.

Vậy bài toán quy về việc tính chiều dài cạnh huyền và cạnh góc vuông lớn của
một tam giác vuông khi biết cạnh góc vuông bé và hiệu giữa cạnh huyền và cạnh góc vuông lớn.

Từ định lí Pythagore, ta có:

$a^{2} = c^{2} - b^{2}$

$a^{2} - {(c - b)}^{2} = c^{2} - b^{2} - {(c - b)}^{2}$

$= c^{2} - b^{2} - (c^{2} - 2 b c + b^{2})$

$= 2 b c - 2 b^{2}$

$= 2 b (c - b)$ .

Vì thế

$b = \frac{a^{2} - {(c - b)}^{2}}{2 (c - b)}$ (1)

$c = b + (c - b)$ (2)

Đem giá trị của a, c-b thay vào hai công thức (1) và (2) sẽ dễ dàng tính được độ sâu của nước là:

$b = \frac{{1,665}^{2} - {0,33}^{2}}{2.0,33} = \frac{2,772225 - 0,1089}{0,66} \approx 4,035$ (m).

Độ cao của cây sậy là: $c = 4,035 + 0,33 = 4,365$ (m).

Câu 4:

Tính bán kính đường tròn ngoại tiếp một tam giác có các cạnh là 50, 50, 60.

Xem đáp án

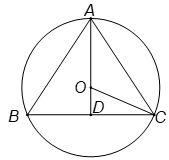
Theo định lí Pythagore, ta có: $A D^{2} = A C^{2} - D C^{2}$ .

Do $D C = B C : 2 = 30$ , nên:

$A D = \sqrt{50^{2} - 30^{2}} = 40$ .

Ta lại có:

$O C^{2} = D C^{2} + {(A D - O A)}^{2}$

$= D C^{2} + A D^{2} - 2 A D . O C + O C^{2}$ .

Do đó: $O C^{2} = \frac{D C^{2} + A D^{2}}{2 A D} = \frac{30^{2} + 40^{2}}{2.40} = \frac{125}{4}$ .

Câu 5:

Dựng một hình vuông có diện tích bằng diện tích một hình chữ nhật cho trước.

Xem đáp án

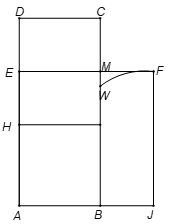
Cho hình chữ nhật ABCD. Ta vẽ hình chữ vuông ABKH trong hình chữ nhật ABCD. Sau đó xác định các trung điểm E và M của DH và CK .

Dựng hình vuông AEFJ đi qua M. Lấy J làm tâm vẽ một đường tròn có bán kính JF cắt BM ở W. Hình vuông có cạnh bằng BW sẽ có diện tích bằng diện tích ABCD vì theo định lí Pythagore ta có:

B W^{2} = J W^{2} - B J^{2}

$= J F^{2} - K M^{2}$

$= (J F - B J) (J F + K M)$

$= A B . B C$ .

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 9: Bài toán thực tế Hình học có đáp án

Chủ đề 1: Định lí PYTHAGORE và những ứng dụng trong các bài toán thực tế có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương