8 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 15

Câu 1:

Với các giá trị nào của m thì hàm số $y = (m^{2} - 4) x + 31$ đồng biến

Xem đáp án

$y = (m^{2} - 4) x + 31$ đồng biến khi $m^{2} - 4 > 0 \Rightarrow [\begin{array}{l} m < - 2 \\ m > 2 \end{array}$

Câu 2:

Với giá trị nào của m thì hàm số $y = (m^{2} - 2) x - 7$ nghịch biến

Xem đáp án

$y = (m^{2} - 2) x - 7$ nghịch biến khi $m^{2} - 2 < 0 \Rightarrow - \sqrt{2} < m < \sqrt{2}$

Câu 3:

Cho đường thẳng $y = m x + 5 (D_{1})$ và đường thẳng $y = - 2 x (D_{2})$ và điểm A(-2; 1)

a) Xác định m biết $(D_{1})$ qua A. Vẽ $(D_{1}); (D_{2})$ trên mặt phẳng tọa độ

b) Viết phương trình đường thẳng $(D_{3})$ biết $(D_{3}) / / (D_{1})$ và $(D_{3})$ cắt $(D_{2}^{})$ tại điểm C có tung độ là -2.

Xem đáp án

a) $A (- 2; 1) \in (D_{1}) \Rightarrow 1 = m . (- 2) + 5 \Leftrightarrow m = 2$ . Học sinh tự vẽ đồ thị $(D_{1}), (D_{2})$

b) Gọi phương trình $(D_{3})$ có dạng $y = a x + b (a \neq 0)$

$(D_{3}) / / (D_{1}) : y = 2 x + 5 \Rightarrow \{\begin{cases} a = 2 \\ b \neq 5 \end{cases}$

$(D_{3})$ cắt $(D_{2})$ tại C có tung độ $- 2 \Rightarrow \{\begin{cases} y_{C} = - 2 \\ \Rightarrow x_{C} = 1 \end{cases}$ . Thay C(1; -2) vào y = ax + b ta có:

$- 2 = 2.1 + b \Rightarrow b = - 4 (t m)$ . Vậy $(D_{3}) : y = 2 x - 4$

Câu 4:

Cho đường thẳng $y = m x + m + 2 (D_{m})$ điểm A(1; 4), đường thẳng y = -x + 4 (d)

a) Xác định m để $(D_{m}) / / (d)$

b) Chứng minh đường thẳng $(D_{m})$ luôn đi qua điểm cố định

c) Tìm trên (d) điểm B sao cho khoảng cách AB ngắn nhất

Xem đáp án

a) $(D_{m}) : y = m x + m + 2 / / (d) : y = - x + 4$ $\Leftrightarrow \{\begin{cases} m = - 1 \\ m + 2 \neq 4 \end{cases} \Leftrightarrow \{\begin{cases} m = - 1 \\ m \neq 2 \end{cases} \Rightarrow m = - 1$

b) Gọi $M (x_{0}; y_{0})$ là điểm mà $(D_{m})$ y = mx + m + 2 luôn đi qua

$\begin{array}{l} \Rightarrow y_{0} = m x_{0} + m + 2 \\ \Leftrightarrow m x_{0} + m = y_{0} + 2 \Leftrightarrow m (x_{0} + 1) = y_{0} + 2 (*) \end{array}$

Phương trình (*) luôn thỏa mãn $\Leftrightarrow \{\begin{cases} x_{0} + 1 = 0 \\ y_{0} + 2 = 0 \end{cases} \Rightarrow \{\begin{cases} x_{0} = - 1 \\ y_{0} = - 2 \end{cases}$

Vậy M(-1; -2) là điểm mà $(D_{m})$ luôn đi qua .

$\begin{array}{l} c) B \in (d) y = - x + 4 \Rightarrow B (x_{B}; 4 - x_{B}) \\ A B = \sqrt{{(x_{A} - x_{B})}^{2} + {(y_{A} - y_{B})}^{2}} = \sqrt{{(1 - x_{B})}^{2} + {(4 - 4 + x_{B})}^{2}} \\ = \sqrt{1 - 2 x_{B} + 2 x_{B}^{2}} \end{array}$

AB ngắn nhất $\Leftrightarrow 2 x_{B}^{2} - 2 x_{B} + 1$ nhỏ nhất

$\Leftrightarrow {(\sqrt{2} x_{B})}^{2} - 2. \sqrt{2} x_{B} . \frac{1}{\sqrt{2}} + \frac{1}{2} + \frac{1}{2}$ nhỏ nhất

$\Leftrightarrow {[\sqrt{2} x_{B} - 1]}^{2} + \frac{1}{2} \geq 0$ $\Rightarrow M i n A B = \frac{1}{2} \Leftrightarrow \sqrt{2} x_{B} - \frac{1}{2} = 0 \Leftrightarrow x_{B} = \frac{\sqrt{2}}{4}$

Vậy $B (\frac{\sqrt{2}}{4}; \frac{16 - \sqrt{2}}{4})$ thì $A B_{\min} = \frac{1}{2}$

Câu 5:

Tìm tọa độ giao điểm đường thẳng sau:

2 x - 3 y = 1

và x - y = 1

Xem đáp án

$\{\begin{cases} 2 x - 3 y = 1 \\ x - y = 1 \end{cases} \Leftrightarrow \{\begin{cases} 2 x - 3 y = 1 \\ 2 x - 2 y = 2 \end{cases} \Leftrightarrow \{\begin{cases} y = 1 \\ x = 2 \end{cases}$

Vậy tọa độ giao điểm là (2; 1)

Câu 6:

Tìm tọa độ giao điểm đường thẳng sau:

3x - y = 3 và x + y = 5

Xem đáp án

$\{\begin{cases} 3 x - y = 3 \\ x + y = 5 \end{cases} \Leftrightarrow \{\begin{cases} 4 x = 8 \\ y = 5 - x \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = 3 \end{cases}$

Vậy tọa độ giao điểm là (2; 3)

Câu 7:

Cho hai đường tròn (O; 12cm) và (O'; 5cm), OO' = 13cm.

a) Chứng tỏ rằng hai đường tròn (O) và (O') cắt nhau tại hai điểm phân biệt

b) Gọi A, B là giao điểm của hai đường tròn (O) và (O'). Chứng minh rằng OA là tiếp tuyến của đường tròn (O'). Tính độ dài AB.

Xem đáp án

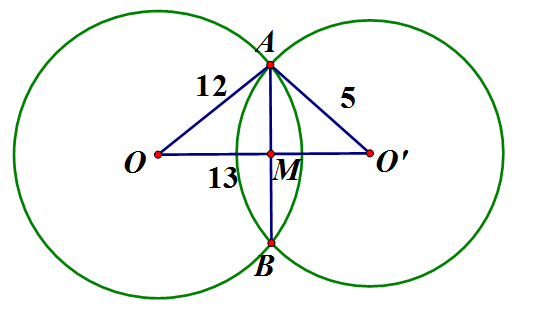
Cho hai đường tròn (O; 12cm) và (O'; 5cm), OO' = 13cm. a) Chứng tỏ rằng (ảnh 1)

a) Ta có: $O A + O' A > O O' (12 + 5 > 13) \Rightarrow (O)$ và (O’) cắt nhau tại 2 điểm phân biệt

b) Ta có: $O A^{2} + O' A^{2} = 5^{2} + 12^{2} = 169 = 13^{2} = O O'^{2}$ $\Rightarrow Δ O A O'$ vuông tại A (định lý Pytago đảo) $\Rightarrow O A ⊥ O' A$

Vì $A \in (O') \Rightarrow O A$ là tiếp tuyến của (O’)

Gọi $M = A B \cap O O'$

Theo tính chất 2 đường tròn cắt nhau $\Rightarrow A B$ là đường trung trực $O O' \Rightarrow M$ là trung điểm $O O' . Δ O A O'$ vuông tại A, có AM đường cao

$\Rightarrow \frac{1}{A M^{2}} = \frac{1}{A O^{2}} + \frac{1}{A O'^{2}}$ (hệ thức lượng) hay $\frac{1}{A M^{2}} = \frac{1}{12^{2}} + \frac{1}{5^{2}} \Rightarrow A M = \frac{60}{13} (c m)$

\Rightarrow A B = 2 A M = 2. \frac{60}{13} = \frac{120}{13} (c m)

Câu 8:

Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Đường thẳng qua A cắt (O) tại B, cắt (O') tại $C (C \neq A)$

a) Chứng minh OB // O'C

b) Gọi d là tiếp tuyến tại B của đường tròn (O), d' là tiếp tuyến tại C của (O'). Chứng minh rằng d // d'.

Xem đáp án

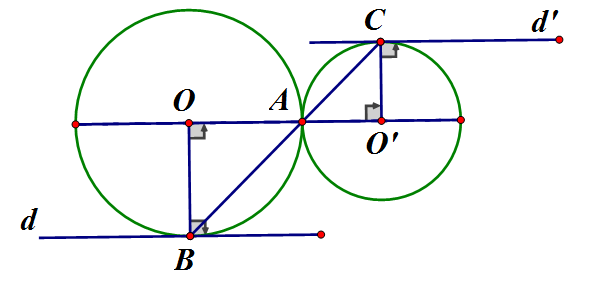
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Đường thẳng qua A cắt (O) (ảnh 1)

a)

O A = O B (= R) \Rightarrow Δ O A B

cân tại O

\Rightarrow \hat{O B A} = \hat{O A B}, c m t t \Rightarrow \hat{O' A C} = \hat{O' C A}

Mà $\hat{O B A} = \hat{O' C A}$ (đối đỉnh), do đó: $\hat{O B A} = \hat{O' C A} \Rightarrow O B / / O' C$

$d ⊥ O B$ (d là tiếp tuyến tại B của (O)) $\Rightarrow O B / / O' C \Rightarrow d ⊥ O' C$ (d' là tiếp tuyến tại (C) của (O')). Do đó d // d'.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập theo tuần Toán 9 - Tuần 15

Bài tập theo tuần Toán 9 - Tuần 15

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương