8 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 35 - Đề 1

Bài tập theo tuần Toán 9 - Tuần 35

Bài tập theo tuần Toán 9 - Tuần 35 - Đề 1

1307 lượt thi
8 câu hỏi
30 phút

Danh sách câu hỏi

Câu 1:

\{\begin{cases} 2 x + y = 5 \\ x - y = 4 \end{cases}

Xem đáp án

$\{\begin{cases} 2 x + y = 5 \\ x - y = 4 \end{cases} \Leftrightarrow \{\begin{cases} 3 x = 9 \\ y = x - 4 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = 1 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất

(x; y) = (3; - 1)

Câu 2:

Cho phương trình bậc hai: $x^{2} - 2 x + m = 0$

a) Xác định các hệ số a, b, c của phương trình

b) Giải phương trình với m = - 8

Xem đáp án

$a) x^{2} - 2 x + m = 0 \Rightarrow a = 1; b = - 2; c = m$

b) Khi m = -8 phương trình thành: $x^{2} - 2 x - 8 = 0 \Leftrightarrow [\begin{array}{l} x = 4 \\ x = - 2 \end{array}$

Vậy $S = \{4; - 2\}$

Câu 3:

Cho hàm số $y = f (x) = x^{2}$ có đồ thị là (P).

Tính f(0) và $f (\sqrt{3})$

Xem đáp án

$f (0) = 0^{2} = 0 f (\sqrt{3}) = {(\sqrt{3})}^{2} = 3$

Câu 4:

Cho hàm số $y = f (x) = x^{2}$ có đồ thị là (P)

Vẽ đồ thị (P)

Xem đáp án

Học sinh tự vẽ

Câu 5:

Cho hàm số $y = f (x) = x^{2}$ có đồ thị là (P)

Gọi N là điểm thuộc đồ thi (P) nói trên và có hoành độ bằng $- \sqrt{3}$ . Hãy tính độ dài đoạn thẳng ON (điểm O là gốc tọa độ, đơn vị đo trên mỗi trục tọa độ là cm)

Xem đáp án

$x_{N} = - \sqrt{3} \Rightarrow y_{N} = {(- \sqrt{3})}^{2} = 3 \Rightarrow N (- \sqrt{3}; 3)$

$\Rightarrow O N = \sqrt{{(- \sqrt{3} - 0)}^{2} + {(3 - 0)}^{2}} = 2 \sqrt{3}$

Câu 6:

Hai số có tổng bằng 24. Nếu tăng số thứ nhất lên gấp 4 lần và tăng số thứ hai lên gấp 3 lần thì tổng của hai số mới bằng 81. Tìm hai số đó

Xem đáp án

Gọi a, b là hai số cần tìm , theo đề ta có hệ phương trình

$\{\begin{cases} a + b = 24 \\ 4 a + 3 b = 81 \end{cases} \Leftrightarrow \{\begin{cases} b = 24 - a \\ 4 a + 3 (24 - a) = 81 \end{cases} \Leftrightarrow \{\begin{cases} a = 9 \\ b = 15 \end{cases}$

Vậy hai số cần tìm là 9 và 15.

Câu 7:

Cho phương trình bậc hai: $x^{2} - (m + 1) x - 1 = 0.$ Xác định m để phương trình có hai nghiệm $x_{1}, x_{2}$ thỏa mãn hệ thức $x_{1} + x_{2} + x_{1} . x_{2} = 2018$

Xem đáp án

$\begin{array}{l} x^{2} - (m + 1) x - 1 = 0 \\ Δ = {(m + 1)}^{2} - 4. (- 1) = m^{2} + 2 m + 5 > 0 \end{array}$

Nên phương trình luôn có hai nghiệm phân biệt, áp dụng Vi et ta có:

$\{\begin{cases} x_{1} + x_{2} = m + 1 \\ x_{1} x_{2} = - 1 \end{cases}$

Ta có:

$\begin{array}{l} x_{1} + x_{2} + x_{1} x_{2} = 2018 \\ h a y m + 1 - 1 = 2018 \Leftrightarrow m = 2018 \end{array}$

Vậy m = 2018 thì $x_{1} + x_{2} + x_{1} x_{2} = 2018$

Câu 8:

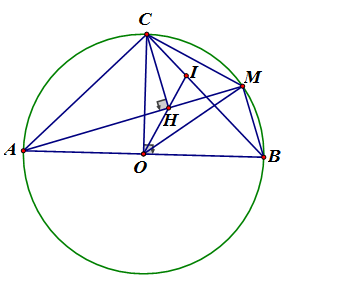
Cho nửa đường tròn (O;R) đường kính AB, bán kính OC vuông góc với AB.Gọi M là một điểm trên cung BC $(M \neq B; M \neq C)$ . Kẻ CH vuông góc với AM tại H

a) Tính diện tích hình quạt ứng với cung AC của nửa đường tròn (O) khi R = 3cm

b) Chứng minh rằng tứ giác OACH nội tiếp trong một đường tròn.

c) Chứng minh rằng OH là tia phân giác của góc MOC

d) Tia OH cắt BC tại điểm I. Chứng minh $O I . A M = R^{2} . \sqrt{2}$

Xem đáp án

Cho nửa đường tròn (O;R) đường kính AB, bán kính OC vuông góc với AB (ảnh 1)

a) Vì $C O ⊥ A B \Rightarrow \hat{C O A} = 90^{0} \Rightarrow S_{q u a t} = \frac{π {.3}^{2} {.90}^{0}}{360^{0}} = \frac{9 π}{4} (c m^{2})$

b) Ta có $\hat{C O A} = \hat{C H A} = 90^{0}$ có 2 đỉnh liên tiếp H, O cùng nhìn cạnh AC dưới 1 góc $90^{0}$ $\Rightarrow C H O A$ là tứ giác nội tiếp

c) Ta có $\hat{C A M} = \hat{C O H}$ (CAOH nội tiếp ) mà $\hat{C A M}$ và $\hat{C O M}$ là góc nội tiếp và góc ở tâm cùng chắn cung CM $\Rightarrow \hat{C O H} = \frac{1}{2} \hat{C O M}$ nên OH là tia phân giác góc COM

d) Ta có: $\hat{C M A} = \frac{1}{2} s d \overset{⏜}{A C} = 45^{0}$

$Δ C O B$ vuông cân $\Rightarrow \hat{O C B} = 45^{0}$

Xét $Δ O I C$ và $Δ A C M$ có:

$\hat{C A M} = \hat{C O I}$ (vì CAOH nội tiếp), $\hat{O C I} = \hat{A M C} = 45^{0}$

$\Rightarrow Δ O I C ~ Δ A C M (g . g) \Rightarrow \frac{O I}{O C} = \frac{A C}{A M} \Rightarrow O I . A M = O C . A C = R . R \sqrt{2} = R^{2} \sqrt{2}$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập theo tuần Toán 9 - Tuần 35

Bài tập theo tuần Toán 9 - Tuần 35 - Đề 1

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương