14 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 10

Câu 1:

Cho hình chữ nhật ABCD có AD = 9,3cm, CD = 12,4cm. Chứng minh rằng bốn điểm A, B, C, Dcùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Xem đáp án

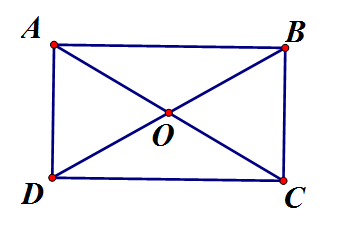
Cho hình chữ nhật ABCD có AD = 9,3cm, CD = 12,4cm. Chứng minh rằng bốn (ảnh 1)

Theo tính chất hình chữ nhật, ta có:

O A = O B = O C = O D \Rightarrow A, B, C, ​ D \in (O)

O A = \frac{1}{2} A C = \frac{1}{2} . \sqrt{A B^{2} + B C^{2}} = \frac{1}{2} . \sqrt{9, 3^{2} + 12, 4^{2}} = 7, 75 (c m)

Câu 2:

Cho một tứ giác ABCD có 2 đường chéo AC, BD vuông góc với nhau. Gọi M, N, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh rằng 4 điểm M, N, R, S cùng nằm trên đường tròn.

Xem đáp án

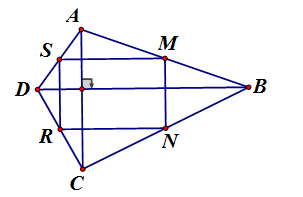
Cho một tứ giác ABCD có 2 đường chéo AC, BD vuông góc với nhau. Gọi (ảnh 1)

$Δ A D B$ có S là trung điểm AD, M là trung diểm AB

$\Rightarrow S M$ là đường trung bình $Δ A D B$

$\Rightarrow S M = \frac{1}{2} D B, S M / / D B$

Chứng minh tương tự $\Rightarrow R N = \frac{1}{2} D B, R S / / B D \Rightarrow S M N R$ là hình bình hành (1)

Mà $S M / / B D, M N / / A C, A C ⊥ B D \Rightarrow S M / / M N (2)$

Từ (1) và (2) suy ra SMNR là hình chữ nhật nên 4 điểm M, N, R, S cùng nằm trên đường tròn

Câu 3:

Cho tam giác ABC nhọn. Vẽ đường tròn (O) có đường kính BC, nó cắt cạnh AB, AC theo thứ tự ở D và E.

a) Chứng minh rằng $C D ⊥ A B, B E ⊥ A C$

b) Gọi K là giao điểm của BE, CD. Chứng minh $A K ⊥ B C$

Xem đáp án

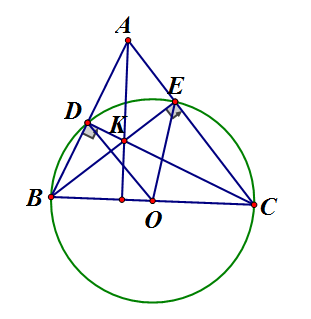
Cho tam giác ABC nhọn. Vẽ đường tròn (O) có đường kính BC, nó cắt cạnh AB (ảnh 1)

a) $Δ B D C$ có $O D = O B = O C = \frac{1}{2} B C \Rightarrow Δ B D C$ vuông tại A (theo định lý đảo đường trung tuyến ứng với cạnh huyền) $\Rightarrow C D ⊥ A B$

Chứng minh tương tự $\Rightarrow B E ⊥ A C$

b) Vì $C D ⊥ A B, B E ⊥ A C, K$ là giao điểm của $B E, C D \Rightarrow K$ là trực tâm $Δ A B C$

nên $A K ⊥ B C$

Câu 4:

Tính bán kính đường tròn ngoại tiếp $Δ A B C$ đều có cạnh là a

Xem đáp án

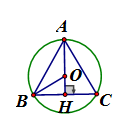
Tính bán kính đường tròn ngoại tiếp tam giác ABC đều có cạnh là a (ảnh 1)

$Δ A B C$ đều cạnh $a \Rightarrow A H = \frac{a \sqrt{3}}{2}$

Theo tính chất trọng tâm : $\Rightarrow R = A O = \frac{2}{3} A H = \frac{a \sqrt{3}}{2} . \frac{2}{3} = \frac{a \sqrt{3}}{3}$

Câu 5:

Cho hình thoi ABCD cạnh a. Gọi R và r lần lượt là bán kính các đường tròn ngoại tiếp tam giác ABD, ABC. Chứng minh rằng: $\frac{1}{R^{2}} + \frac{1}{r^{2}} = \frac{4}{a^{2}}$

Xem đáp án

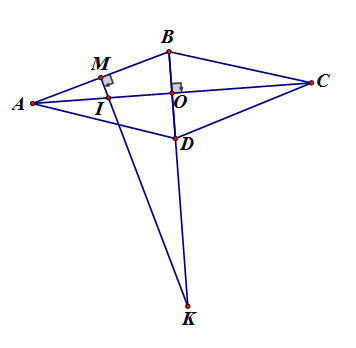
Cho hình thoi ABCD cạnh a. Gọi R và r lần lượt là bán kính các đường tròn (ảnh 1)

Gọi M, I, K là giao điểm của đường trung trực AB với AB, AC, BD, O là giao điểm của AC và BD.

Ta có: $O A = O C, O B = O D, A C ⊥ B D$ (Vì ABCD là hình thoi)

Nên AC là trung trực của BD, BD là trung trực của AC

Do đó I, K lần lượt là tâm đường tròn ngoại tiếp $Δ A D B, Δ A B C$ $\Rightarrow I A = R, K B = r$

Xét $Δ O A B$ và $Δ M K B$ có $\hat{A B O}$ chung, $\hat{A O B} = \hat{K M B} (= 90^{0})$

Do đó: $Δ O A B ~ Δ M K B$

$\Rightarrow \frac{O B}{M B} = \frac{A B}{K B} \Rightarrow \frac{O B}{\frac{a}{2}} = \frac{a}{r} \Rightarrow O B^{2} = {(\frac{a^{2}}{2 r})}^{2} = \frac{a^{4}}{4 r^{2}}$

Tương tự ta có: $O A^{2} = \frac{a^{2}}{4 R^{2}}$

$Δ O A B$ vuông tại O, theo định lý Pytago ta có:

$O A^{2} + O B^{2} = A B^{2} \Rightarrow \frac{a^{4}}{4 R^{2}} + \frac{a^{4}}{4 R^{2}} = a^{2} \Rightarrow \frac{1}{R^{2}} + \frac{1}{r^{2}} = \frac{4}{a^{2}} (d f c m)$

Câu 6:

Cho hàm số $y = f (x) = - \frac{2}{15} x$ . Tính $f (- 12); f (0); f (- 5)$

Xem đáp án

$\begin{array}{l} y = f (x) = \frac{- 2}{15} x; f (- 12) = \frac{- 2}{15} . (- 12) = \frac{8}{5} \\ f (0) = \frac{- 2}{15} .0 = 0 f (- 5) = \frac{- 2}{15} . (- 5) = \frac{2}{3} \end{array}$

Câu 7:

Cho hàm số $y = f (x) = 3 x^{4} .$

a) Tính $f (- 1); f (1); f (a)$

b) Chứng minh rằng: f(x) = f(-x)

Xem đáp án

$\begin{array}{l} a) f (- 1) = 3. {(- 1)}^{4} = 3; f (1) = {3.1}^{4} = 3 f (a) = 3 a^{4} \\ b) f (x) = 3 x^{4}; f (- x) = 3. {(- x)}^{4} = 3 x^{4} \Rightarrow f (x) = f (- x) \end{array}$

Câu 8:

Chứng minh rằng $y = f (x) = 88 x + 1963, x \in ℝ$ hàm số đồng biến

Xem đáp án

$a = 88 > 0 \Rightarrow y = f (x) = 88 x + 1963$ đồng biến

Câu 9:

Chứng minh rằng hàm số $y = f (x) = 4 - \frac{2}{5} x, x \in ℝ$ nghịch biến

Xem đáp án

$a = \frac{- 2}{5} < 0 \Rightarrow y = f (x) = 4 - \frac{2}{5} x$ nghịch biến

Câu 10:

Tìm TXĐ của hàm số sau:

y = \frac{3 x}{x^{2} - 4} + \sqrt{x - 1}

Xem đáp án

$y = \frac{3 x}{x^{2} - 4} + \sqrt{x - 1}$ xác định $\Leftrightarrow \{\begin{cases} x^{2} - 4 \neq 0 \\ x - 1 \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq 2 \\ x \geq 1 \end{cases}$

Câu 11:

Tìm TXĐ của hàm số sau:

$y = \sqrt{x^{2} - 6 x + 5}$

Xem đáp án

$y = \sqrt{x^{2} - 6 x + 5}$ có nghĩa $\Leftrightarrow x^{2} - 6 x + 5 \geq 0 \Leftrightarrow (x - 1) (x - 5) \geq 0 \Leftrightarrow [\begin{array}{l} x \leq 1 \\ x \geq 5 \end{array}$

Câu 12:

Tìm TXĐ của hàm số sau:

y = \frac{1 + x}{|x - 2| - |x + 1|}

Xem đáp án

$y = \frac{1 + x}{|x - 2| - |x + 1|}$ có nghĩa $\Leftrightarrow |x - 2| \neq |x - 1| \Leftrightarrow 2 - x \neq x - 1 \Leftrightarrow x \neq \frac{3}{2}$

Câu 13:

Tìm TXĐ của hàm số sau:

y = \sqrt{5 - \sqrt{x - 2}}

Xem đáp án

$y = \sqrt{5 - \sqrt{x - 2}}$ có nghĩa $\{\begin{cases} 5 - \sqrt{x - 2} \geq 0 \\ x - 2 \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} x - 2 \leq 25 \\ x \geq 2 \end{cases} \Leftrightarrow 2 \leq x \leq 27$

Câu 14:

Chứng minh rằng hàm số $y = x^{3} - x^{2} + x - 6$ đồng biến trên $ℝ$

Xem đáp án

$y = x^{3} - x^{2} + x - 6 = x (x^{2} - x + 1) - 6$

Ta có $a = x^{2} - x + 1 = {(x - \frac{1}{2})}^{2} + \frac{3}{4} > 0$

$\Rightarrow y = x^{3} - x^{2} + x - 6$ đồng biến trên $ℝ$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập theo tuần Toán 9 - Tuần 10

Bài tập theo tuần Toán 9 - Tuần 10

Danh sách câu hỏi

Có thể bạn quan tâm

Các bài thi hot trong chương