Bài tập theo tuần Toán 9 - Tuần 11
-
885 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số bậc nhất Tìm các giá trị của m để hàm số
a) Đồng biến
b) Nghịch biến
Cho hàm số bậc nhất:
a) Hàm số (1) đồng biến khi
b) Hàm số (1) nghịch biến khi
Câu 2:
Cho hai hàm số và Chứng minh rằng:
a) Hàm số là các hàm số đồng biến
b) Hàm số f(x) - g(x) là hàm số nghịch biến.
Ta có
Hàm số f(x) + g(x) đồng biến.
Ta có
Hàm số đồng biến
Ta có
Vì hàm số f(x) - g(x) đồng biến
Vì
f(x) - g(x) nghịch biến
Câu 3:
Với các giá trị nào của m thì hàm số sau là hàm số bậc nhất:
là hàm số bậc nhất khi
Câu 4:
là hàm số bậc nhất khi
Câu 7:
Cho tam giác ABC nhọn các đường cao BD, CE cắt nhau tại H
a) CMR: B, E, D, C cùng thuộc một đường tròn
b) CMR: A, D, H, E cùng thuộc một đường tròn
c) CMR:
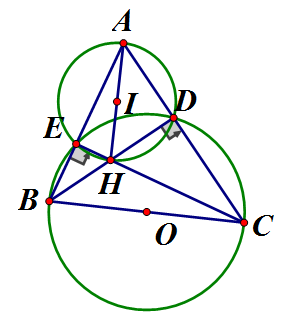
Gọi I là trung điểm AH. Theo tính chất đường trung tuyến trong tam giác vuông
đường trong (I; IA)
Trong (O) ta có BC là đường kính, DE là dây cung
Trong (I) ta có AH là đường kính, DE là dây cung nên
Câu 8:
Cho đường tròn (O; R), A và B thuộc (O) sao cho Gọi M là trung điểm AB.
a) Chứng minh
b) Tính độ dài AB, OM theo R
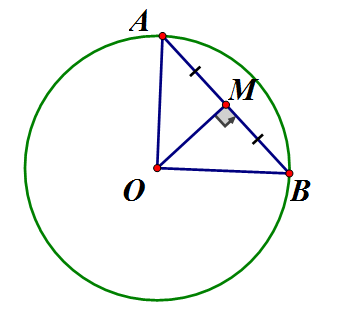
a) Ta có AB là dây cung, M là trung điểm (tính chất đường kính dây cung)
b) vuông cân tại O
vuông tại O có OM là đường trung tuyến
Câu 9:
Cho đường tròn (O; R), A và B di động trên đường tròn (O) thỏa mãn Vẽ tại H
a) Chứng minh H là trung điểm của AB
b) Tính OH, AB. Diện tích theo R
c) Tia OH cắt (O; R) tại C. Tứ giác OACB là hình gì ? Vì sao ?
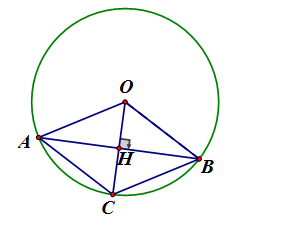
a) Ta có AB là dây cung mà là trung điểm AB (tính chất đường kính – dây cung)
b) cân tại O (OA = OB = R), có OH là đường cao là đường phân giác
vuông tại H có đều
và
là trung điểm OC
c) Tứ giác OACB có hai đường chéo OC, AB vuông góc nhau tại trung điểm mỗi đường là hình thoi
Câu 10:
Cho đường tròn (O; R) và một dây cung AB. Gọi I là trung điểm của AB. Tia OI cắt cung AB tại M
a) Cho Tính độ dài dây cung MA
b) Gọi N là điểm đối xứng của M qua O, giả sử Tính bán kính R.
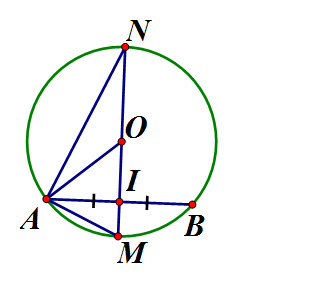
a) Vì I là trung điểm của AB (tính chất đường kính dây cung)
Vì
vuông tại I, theo định lý Pytago
vuông tại I, theo định lý Pytago
Vậy
b) vuông tại I, áp dụng định lý Pytago
