35 câu hỏi trắc nghiệm thuộc 160 câu trắc nghiệm Phương pháp tọa độ trong mặt phẳng (P6)

Câu 1:

Cho elip có phương trình: $\frac{x^{2}}{4} + \frac{y^{2}}{1} = 1$ Khi đó tọa độ hai đỉnh trên trục lớn của elip là.

A. A₁( -1; 0) và A₂( 1;0)

B. A₁( 0; -1) và A₂( 0; 1)

C. A₁( 2;0) và A₂( 1; 0)

D. A₁( (-2;0) và A₂(2;0)

Xem đáp án

Ta có: a²= 4 mà a> 0 nên a= 2

- Hai đỉnh trên trục lớn là: . A₁( (-2;0) và A₂(2;0)

Chọn D

Câu 2:

Cho elip có phương trình: $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ Khi đó tọa độ hai đỉnh trên trục nhỏ của elip là.

A. B₁( 0; -2) và B₂( 0;2)

B. B₁( -2;0) và B₂( 2; 0)

C. B₁( -3;0) và B₂( -2;0)

D. B₁( 0;3) và B₂(0;-3)

Xem đáp án

Ta có: b²= 4 mà b> 0 nên b= 2

- Hai đỉnh trên trục nhỏ là: B₁( 0; -2) và B₂( 0;2)

Chọn A

Câu 3:

Trong mặt phẳng với hệ trục tọa độ Oxy cho elip (E) có độ dài trục lớn bằng 12 và độ dài trục bé bằng 6. Phương trình

nào sau đây là phương trình của elip (E) .

A. $\frac{x^{2}}{144} + \frac{y^{2}}{36} = 1$

B. $\frac{x^{2}}{9} + \frac{y^{2}}{36} = 1$

C. $\frac{x^{2}}{36} + \frac{y^{2}}{9} = 1$

D. $\frac{x^{2}}{144} + \frac{y^{2}}{36} = 0$

Xem đáp án

Phương trình chính tắc của elip có dạng : $(E) \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a, b > 0)$

Ta có :

+ Độ dài trục lớn là 12 nên 2a= 12 => a= 6 .

+ Độ dài trục bé là 6 nên 2b = 6 => b= 3

Vậy phương trình của Elip là: $\frac{x^{2}}{36} + \frac{y^{2}}{9} = 1$ .

Chọn C.

Câu 4:

Trong mặt phẳng với hệ trục tọa độ Oxy cho elip ( E) có độ dài trục lớn bằng 10 và độ dài tiêu cự bằng 6 . Phương

trình nào sau đây là phương trình của elip (E).

A. $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$

B. $\frac{x^{2}}{16} + \frac{y^{2}}{25} = 1$

C. $\frac{x^{2}}{36} + \frac{y^{2}}{9} = 1$

D. $\frac{x^{2}}{144} + \frac{y^{2}}{36} = 0$

Xem đáp án

Ta có: độ dài trục lớn là 10 nên 2a= 10 => a= 5.

Độ dài tiêu cự là 6 nên 2c= 6 => c= 3

Ta có: b²= a²- c²= 25- 9= 16 => b= 4

Vậy phương trình của Elip là: $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$

Chọn A.

Câu 5:

Trong mặt phẳng với hệ trục tọa độ Oxy cho elip (E) có độ dài trục nhỏ bằng 8 và độ dài tiêu cự bằng 10 Phương

trình nào sau đây là phương trình của elip (E)

A. $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$

B. $\frac{x^{2}}{16} + \frac{y^{2}}{41} = 1$

C. $\frac{x^{2}}{36} + \frac{y^{2}}{9} = 1$

D. $\frac{x^{2}}{41} + \frac{y^{2}}{16} = 1$

Xem đáp án

Ta có: độ dài trục nhỏ là 8 nên 2b = 8 => b= 4.

Độ dài tiêu cự là 10 nên 2c = 10 => c= 5.

Lại có : a²= b²+ c²= 16+ 25= 41

Vậy phương trình của Elip là: $\frac{x^{2}}{41} + \frac{y^{2}}{16} = 1$

Chọn D.

Câu 6:

Trong mặt phẳng với hệ trục tọa độ Oxy; phương trình (E) đi qua điểm $M (0; 3), N (3; - \frac{12}{5})$ là:

A. $\frac{x^{2}}{6} + \frac{y^{2}}{3} = 1$

B. $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$

C. $\frac{x^{2}}{5} + \frac{y^{2}}{3} = 1$

D. $\frac{x^{2}}{36} + \frac{y^{2}}{9} = 1$

Xem đáp án

Phương trình elip có dạng:

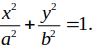
Đi qua hai điểm M; N ta được:

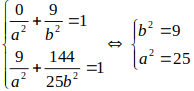
Vậy phương trình elip:

Chọn B.

Câu 7:

Cho elíp $(E) : \frac{x^{2}}{16} + \frac{y^{2}}{9} = 1$ và đường thẳng d: 3x+ 4y -12= 0. Số giao điểm của đường thẳng d và elip (E) là:

A. 0

B.1

C. 2

D. 3

Xem đáp án

Ta có d: 3x+ 4y -12= 0 $\Leftrightarrow y = 3 - \frac{3 x}{4}$ , thay vào phương trình $(E) : \frac{x^{2}}{16} + \frac{y^{2}}{9} = 1$ ta được

=> $2 x^{2} - 8 x = 0$

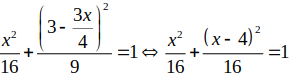
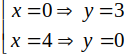
Vậy d luôn cắt (E) tại hai điểm phân biệt A(0;3) và B(4;0).

Chọn C

Câu 8:

Cho Elip (E) : $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ Đường thẳng d: x+ 4= 0 cắt (E) tại hai điểm M; N . Khi đó:

A. $M N = \frac{9}{25}$

B. $M N = \frac{18}{25}$

C. $M N = \frac{18}{5}$

D. $M N = \frac{9}{5}$

Xem đáp án

Xét d: x+4= 0 $\Leftrightarrow x = - 4$ Thay vào (E), ta được:

$\frac{{(- 4)}^{2}}{25} + \frac{y^{2}}{9} = 1 \Leftrightarrow y^{2} = \frac{81}{25} \Leftrightarrow y = \frac{9}{5} h o ặ c y = - \frac{9}{5}$

Do đó giao điểm của đường thẳng d với (E) là hai điểm M ( -4; $\frac{9}{5}$ ) và N ( -4; $- \frac{9}{5}$ )

Khi đó MN = $\sqrt{{(\frac{9}{5} + \frac{9}{5})}^{2}} = \frac{18}{5}$

Chọn C.

Câu 9:

Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và có tiêu cự bằng $4 \sqrt{3}$

A.

B.

C.

D.

Xem đáp án

Gọi phương trình chính tắc của Elip

.

Do độ dài trục lớn gấp đôi trục bé nên 2a= 2( 2b) .

Theo giả thiết ta có

$\{\begin{array}{l} 2 a = 2.2 b \\ 2 c = 4 \sqrt{3} \end{array} \Rightarrow \{\begin{cases} a^{2} = 4 b^{2} \\ a^{2} - b^{2} = 12 \end{cases} \Rightarrow \{\begin{cases} a^{2} = 16 \\ b^{2} = 4 \end{cases}$

Vậy phương trình( E) cần tìm là:

$\frac{x^{2}}{16} + \frac{y^{2}}{4} = 1$

_{Chọn D.}

Câu 10:

Cho Elip $\frac{x^{2}}{5} + \frac{y^{2}}{4} = 1$ . Tính tỉ số của tiêu cự với độ dài trục lớn của Elip.

A. $\frac{\sqrt{5}}{4}$

B. $\frac{\sqrt{5}}{5}$

C. $\frac{3 \sqrt{5}}{5}$

D. $\frac{2 \sqrt{5}}{5}$

Xem đáp án

Gọi phương trình chính tắc của Elip có dạng

.

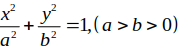Elip $\frac{x^{2}}{5} + \frac{y^{2}}{4} = 1$ có a²= 5; b²= 4 => c²= 5-4= 1 => c= 1

Độ dài trục lớn: $2 a = 2 \sqrt{5}$ và tiêu cự: 2c= 2

Tỉ số $e = \frac{2 c}{2 a} = \frac{1}{\sqrt{5}}$

Chọn B.

Câu 11:

Cho Elip có phương trình : 9x²+ 25y²= 225. Lúc đó hình chữ nhật cơ sở có diện tích bằng

A. 20

B. 35

C. 60

D. 40

Xem đáp án

Ta có

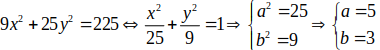
Độ dài trục lớn ( chiều dài hình chữ nhật cơ sở ): 2a= 10 .

Độ dài trục nhỏ ( chiều rộng hình chữ nhật cơ sở : 2b= 6

Diện tích hình chữ nhật cơ sở là 2a. 2b= 10.6= 60 .

Chọn C.

Câu 12:

Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là M(4;3)

A.

B.

C.

D.

Xem đáp án

Gọi phương trình chính tắc của Elip có dạng

Các đỉnh của hình chữ nhật cơ sở có tọa độ: (a; b) ; (a; -b) ; ( -a; b) và (-a; -b)

Ta có M( 4;3) là một đỉnh của hình chữ nhật cơ sở nên chọn

.

_{=> phương trình chính tắc của (E) là}

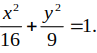
_{Chọn A.}

Câu 13:

Tìm phương trình chính tắc của Elip đi qua điểm (6; 0) và có tâm sai bằng 1/2

A.

B.

C.

D.

Xem đáp án

Do tâm sai của ( E) là 1/2 nên

mà Elip qua điểm (6;0) nên a= 6

=> c= 3 => b²= a²- c²= 36- 9= 27

Vậy

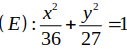
Chọn A.

Câu 14:

Trong các phương trình sau, phương trình nào biểu diễn một elíp có khoảng cách giữa các đường chuẩn là 50/3 và

tiêu cự 6?

A.

B.

C.

D.

Xem đáp án

Ta có: Tiêu cự 2c= 6 => c= 3

Khoảng cách giữa 2 đường chuẩn .

$\frac{2 a}{e} = \frac{50}{3}$

=> 6a²= 50 c nên a²= 25 => b²= 16

_{Vậy phương trình (E) cần tìm là:}

_{Chọn C.}

Câu 15:

Cho elíp có phương trình 16x²+ 25y²= 100.Tính tổng khoảng cách từ điểm thuộc elíp có hoành độ x= 2 đến hai

tiêu điểm.

A. $\sqrt{3}$

B. $2 \sqrt{2}$

C. 5

D. $4 \sqrt{3}$

Xem đáp án

Ta có:

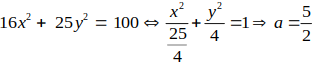
Tổng khoảng cách từ 1 điểm thuộc Elip đến 2 tiêu điểm bẳng 2a= 5.

Chọn C.

Câu 16:

Cho Elip (E) $\frac{x^{2}}{16} + \frac{y^{2}}{12} = 1$ và điểm M nằm trên (E) . Nếu điểm M có hoành độ bằng 1 thì các khoảng cách từ M tới 2

tiêu điểm của (E) bằng

A. $4 \pm \sqrt{2}$

B. 3 và 5.

C. 3,5 và 4,5

D. $4 \pm \frac{\sqrt{2}}{2}$

Xem đáp án

Ta có a²= 16 và b²= 12 nên c²= 16-12= 4

=> 2 tiêu cự là F₁( -2;0) và F₂( 2;0)

Điểm M thuộc (E) và

Từ đó

Chọn C

Câu 17:

Đường thẳng nào dưới đây là 1 đường chuẩn của Elip $\frac{x^{2}}{16} + \frac{y^{2}}{12} = 1$

A. $x + \frac{4}{3} = 0$

B. x+ 2= 0

C. $x - \frac{3}{4} = 0$

D. x+ 8= 0

Xem đáp án

_{Ta có}: a²= 16; b²= 12 nên c²= 16-12= 4

_{=> c = 2}

Đường chuẩn .

Chọn D.

Câu 18:

Một elip có trục lớn bằng 26, tâm sai e =12/13. Trục nhỏ của elip có độ dài bằng bao nhiêu?

A. 10.

B. 12.

C. 24.

D. 5.

Xem đáp án

Ta có a= 13, mà

Suy ra

Dộ dài trục nhỏ là 2b= 10.

Chọn A.

Câu 19:

Lập phương trình chính tắc của elip có tâm O, hai trục đối xứng là hai trục toạ độ và qua hai điểm $M (- 2 \sqrt{3}; \frac{3}{2}); N (2; \frac{3 \sqrt{3}}{2})$

A.

B.

C.

D.

Xem đáp án

Gọi phương trình chính tắc elip cần tìm là

.

Do elip đi qua

,

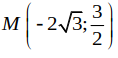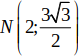
nên ta có hệ

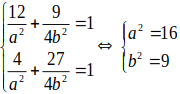
Vậy elip cần tìm là

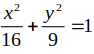
Chọn C.

Câu 20:

Cho elip $(E) : \frac{x^{2}}{169} + \frac{y^{2}}{144} = 1$ và điểm M nằm trên (E). Nếu M có hoành độ bằng - 13 thì khỏang cách từ M đến hai tiêu điểm bằng

A. 10 và 6.

B. 8 và 18.

C. 13 $\pm \sqrt{5}$ .

D. 13 $\pm \sqrt{10}$ .

Xem đáp án

Từ dạng của elip

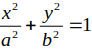ta có .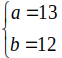

=> c²= a²- b²= 13²- 12²= 25 => c= 5.

Tâm sai của elip

.

MF₁= a+ e.x_M= 8 và MF₂= a- e.x_M= 18

Chọn B.

Câu 21:

Tâm sai của elip $\frac{x^{2}}{16} + \frac{y^{2}}{7} = 1$ bằng

A. $\frac{3}{4}$

B. 2

C. $\frac{\sqrt{7}}{4}$

D. 3

Xem đáp án

Từ dạng của elip

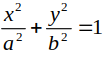ta có .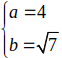

Khi đó ; c²= a²- b² = 9 nên c=3 .

Tâm sai của elip: $e = \frac{c}{a} = \frac{3}{4}$

Chọn A.

Câu 22:

Hypebol $\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1$ có hai tiêu điểm là :

A. F₁( -5;0) và F₂(5;0)

B. F₁( -2;0) và F₂(2;0)

C. F₁( - 3;0) và F₂(3;0)

D. F₁( -4;0) và F₂(4;0)

Xem đáp án

Chọn A.

Ta có: $[\begin{matrix} a^{2} = 16 \\ b^{2} = 9 \\ c^{2} = a^{2} + b^{2} \end{matrix}$ $\Rightarrow [\begin{matrix} a = 5 \\ b = 3 \\ c = 5 \end{matrix}$

Các tiêu điểm là F₁( -5;0) và F₂(5;0).

Câu 23:

Đường thẳng nào dưới đây là đường chuẩn của Hyperbol $\frac{x^{2}}{16} - \frac{y^{2}}{12} = 1$

A. $x - \frac{3}{4} = 0$

B. x+2=0

C. x-4=0

D. $x + \frac{8 \sqrt{7}}{7} = 0$

Xem đáp án

Đáp án : D

Ta có $[\begin{matrix} a^{2} = 16 \\ b^{2} = 12 \\ c^{2} = a^{2} + b^{2} \end{matrix}$ $\Rightarrow$ $[\begin{matrix} a = 4 \\ b = 2 \sqrt{3} \\ c = 2 \sqrt{7} \end{matrix}$

Tâm sai $e = \frac{c}{a} = \frac{2 \sqrt{7}}{4} = \frac{\sqrt{7}}{2}$ . Đường chuẩn: $x + \frac{a}{e} = 0 \Leftrightarrow x + \frac{4}{\frac{\sqrt{7}}{2}} = 0 \Leftrightarrow x + 8 \sqrt{7} = 0$ và $x - 8 \sqrt{7} = 0$ .

Câu 24:

Hypebol có nửa trục thực là 4, tiêu cự bằng 10 có phương trình chính tắc là:

A.

B.

C.

D.

Xem đáp án

Chọn B

Ta có $[\begin{matrix} a = 4 \\ 2 c = 10 \\ b^{2} = c^{2} - a^{2} \end{matrix}$ $\Rightarrow$ $[\begin{matrix} a = 4 \\ c = 5 \\ b = 3 \end{matrix}$

Phương trình chính tắc của Hyperbol là

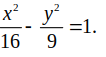
Câu 25:

Tìm phương trình chính tắc của Hyperbol mà hình chữ nhật cơ sở có một đỉnh là (2;-3)

A.

B.

C.

D.

Xem đáp án

Chọn B.

Gọi (H): $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ .

Tọa độ đỉnh của hình chữ nhật cơ sở là A(a; b); B( a; -b); C( -a; b) và D( –a; -b).

Hình chữ nhật cơ sở của (H) có một đỉnh là (2;-3),

suy ra $[\begin{matrix} a = 2 \\ b = 3 \end{matrix}$ .

Phương trình chính tắc của (H) là

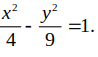
Câu 26:

Đường Hyperbol $\frac{x^{2}}{16} - \frac{y^{2}}{9} = 1$ có một tiêu điểm là điểm nào dưới đây ?

A. $(\sqrt{7}; 0)$

B. $(0; \sqrt{7})$

C. (0;5)

D. (-5; 0)

Xem đáp án

Ta có

$[\begin{matrix} a^{2} = 16 \\ b^{2} = 9 \\ c^{2} = a^{2} + b^{2} \end{matrix}$ $\Rightarrow$ c=5

Các tiêu điểm của (H) là (-5;0) và (5;0) .

Câu 27:

Tâm sai của Hyperbol $\frac{x^{2}}{5} - \frac{y^{2}}{4} = 1$ bằng :

A. $\frac{3}{\sqrt{5}}$

B. $\frac{3}{5}$

C. $\frac{\sqrt{5}}{5}$

D. $\frac{4}{5}$

Xem đáp án

Chọn A

Ta có $[\begin{matrix} a^{2} = 5 \\ b^{2} = 4 \\ c^{2} = a^{2} + b^{2} \end{matrix}$ $\Rightarrow$ $[\begin{matrix} a = \sqrt{5} \\ b = 2 \\ c = 3 \end{matrix}$

=> $c = \frac{e}{a} = \frac{3}{\sqrt{5}}$

Câu 28:

Hypebol 3x²- y²= 12 có tâm sai là:

A. $e = \frac{1}{\sqrt{3}}$

B. $e = \frac{1}{2}$

C. e=2

D. $e = \sqrt{3}$

Xem đáp án

Chọn C.

Ta có: $3 x^{2} - y^{2} = 12 \Rightarrow \frac{x^{2}}{4} - \frac{y^{2}}{12} = 1$

$[\begin{matrix} a^{2} = 4 \\ b^{2} = 12 \\ c^{2} = a^{2} + b^{2} \end{matrix}$ $\Rightarrow$ $[\begin{matrix} a = 2 \\ b = 2 \sqrt{3} \\ c = 4 \end{matrix}$

=> $e = \frac{c}{a} = 2$

Câu 29:

Đường Hyperbol $\frac{x^{2}}{20} - \frac{y^{2}}{16} = 1$ có tiêu cự bằng :

A.12

B.2

C.4

D. 6

Xem đáp án

Chọn A.

Ta có : $a^{2} = 20 b^{2} = 16 c^{2} = a^{2} + b^{2}$ $\Rightarrow$ $[\begin{matrix} a = 2 \sqrt{5} \\ b = 4 \\ c = 6 \end{matrix}$

Khi đó, tiêu cự là 2c = 2.6 = 12

Câu 30:

Tìm phương trình chính tắc của hyperbol nếu nó có tiêu cự bằng 12 và độ dài trục thực bằng 10.

A.

B.

C.

D.

Xem đáp án

Chọn A

Ta có $[\begin{matrix} 2 c = 12 \\ 2 a = 10 \\ b^{2} = c^{2} - a^{2} \end{matrix}$ $\Rightarrow$ $[\begin{matrix} c = 6 \\ a = 5 \\ b^{2} = 11 \end{matrix}$

Phương trình chính tắc (H) $\frac{x^{2}}{25} - \frac{y^{2}}{11} = 1$

Câu 31:

Tìm góc giữa 2 đường tiệm cận của hyperbol $\frac{x^{2}}{3} - y^{2} = 1$

A. 45⁰

B. 30⁰

C.90⁰

D. 60⁰

Xem đáp án

Chọn D.

Ta có $[\begin{matrix} a^{2} = 3 \\ b^{2} = 1 \end{matrix}$ $\Rightarrow$ $[\begin{matrix} a = \sqrt{3} \\ b = 1 \end{matrix}$ :

Đường tiệm cận của (H) là $y = \frac{1}{\sqrt{3}} x$ và $y = - \frac{1}{\sqrt{3}} x$ hay $x - \sqrt{3} y = 0$ và $x + \sqrt{3} y = 0$ .

Gọi là góc giữa hai đường tiệm cận, ta có

$\cos a = |\frac{1.1 - \sqrt{3} . \sqrt{3}}{\sqrt{1^{2} + {(- \sqrt{3})}^{2}} . \sqrt{1^{2} + {\sqrt{3}}^{2}}}| = \frac{1}{2} \Rightarrow a = 60^{0}$

Câu 32:

Hypebol $\frac{x^{2}}{4} - \frac{y^{2}}{9} = 1$ có

A. Hai đỉnh A( -2; 0) và B( 2;0) và tâm sai $e = \frac{2}{\sqrt{13}}$ .

B. Hai đường tiệm cận $y = \pm \frac{2}{3} x$ và tâm sai $e = \frac{\sqrt{13}}{2}$ .

C. Hai đường tiệm cận $y = \pm \frac{3}{2} x$ và tâm sai $e = \frac{\sqrt{13}}{2}$ .

D. Hai tiêu điểm F₁(-2;0) và F₂(2;0) và tâm sai $e = \frac{2}{\sqrt{13}}$ .

Xem đáp án

Chọn C.

Ta có : $[\begin{matrix} a^{2} = 4 \\ b^{2} = 9 \\ c^{2} = a^{2} + b^{2} \end{matrix}$ $\Rightarrow$ $[\begin{matrix} a = 2 \\ b = 3 \\ c = \sqrt{13} \end{matrix}$

Tọa độ đỉnh A(-2 ;0) và B( 2 ;0) tâm sai $e = \frac{c}{a} = \frac{\sqrt{13}}{2}$ ,

hai tiêu điểm $F_{1} (- \sqrt{13}; 0)$ và $F_{2} (\sqrt{13}; 0)$ , hai đường tiệm cận $y = \pm \frac{3}{2} x$ .

Câu 33:

Phương trình hai tiệm cận $y = \pm \frac{2}{3} x$ là của hypebol có phương trình chính tắc nào sau đây?

A.

B.

C.

D.

Xem đáp án

Chọn D.

Ta có: $\pm \frac{b}{a} = \pm \frac{2}{3}$ $\Rightarrow$ $[\begin{matrix} a = 3 \\ b = 2 \end{matrix}$ .

Phương trình (H) : $\frac{x^{2}}{9} - \frac{y^{2}}{4} = 1$

Câu 34:

Đường Hyperbol $\frac{x^{2}}{5} - \frac{y^{2}}{4} = 1$ có tiêu cự bằng :

A.2

B. 6

C. 3

D. 1

Xem đáp án

Chọn B.

Ta có: $[\begin{matrix} a^{2} = 5 \\ b^{2} = 4 \\ c^{2} = a^{2} + b^{2} \end{matrix}$ $\Rightarrow$ $[\begin{matrix} a = \sqrt{5} \\ b = 2 \\ c = 3 \end{matrix}$