18 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 22 - qa.haylamdo.com

Bài tập theo tuần Toán 9 - Tuần 22

Đề số 1

Bài tập theo tuần Toán 9 - Tuần 22

450 lượt thi
18 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Một ô tô đi quãng đường AB với vận tốc 50km/h rồi đi tiếp quãng đường BC với vận tốc 45km/h. Biết quãng đường tổng cộng dài 165km và thời gian ô tô đi trên quãng đường AB ít hơn thời gian đi trên quãng đường BC là 30 phút. Tính thời gian ô tô đi trên mỗi đoạn đường.

Gọi thời gian ô tô đi trên AB, BC lần lượt là x, y (x, y > 0)

Quãng đường AB: 50x, quãng đường $B C = 45 y \Rightarrow 50 x + 45 y = 165 (1)$

Vì thời gian đi trên AB ít hơn trên BC là $30' = \frac{1}{2} h \Rightarrow x - y = - \frac{1}{2} (2)$

Từ (1) và (2) ta có hệ phương trình: $\{\begin{cases} x - y = - \frac{1}{2} \\ 50 x + 45 y = 165 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{3}{2} \\ y = 2 \end{cases} (t m)$

Vậy ô tô đi trên AB hết $\frac{3}{2} h,$ trên BC hết 2h

Câu 2:

Một đội công nhân theo kế hoạch mỗi ngày là 400 chi tiết máy. Do cải tiến kỹ thuật nên mỗi ngày làm được 520 chi tiết máy, vì vậy đội không những xong kế hoạch trước 2 ngày mà còn làm được thêm 40 chi tiết máy. Tính thời gian và tổng số chi tiết máy mà đội công nhân phải làm theo kế hoạch

Gọi x là thời gian đội làm theo kế hoạch, y là thời gian thực tế (x > y > 2)

Vì thực tế xong trước 2 ngày nên x - y = 2 (1)

Số sản phẩm dự định: 400x số sản phẩm thực tế: 520y. Vì làm thêm 40 chi tiết nên 400x - 520y = -40 (2)

Từ $(1), (2) \Rightarrow \{\begin{cases} x - y = 2 \\ 400 x - 520 y = - 40 \end{cases} \Leftrightarrow \{\begin{cases} x = 9 \\ y = 7 \end{cases} (t m)$

Vậy theo kế hoạch thời gian là 7 ngày, số sản phẩm dự định:400.7 = 2800 (chi tiết)

Câu 3:

Một bè gỗ thả trôi sông từ A. Sau khi bè gỗ trôi được 3 giờ 20 phút, một người chèo thuyền từ A đuổi theo và đi được 10km thì gặp bè gỗ. Tính vận tốc của bè gỗ, biết vận tốc người chèo thuyền lớn hơn vận tốc bè gỗ là 4km/h

Gọi x (km/h) là vận tốc chèo (x > 4)

y (km/h) là vận tốc bè gỗ (y > 4)

Vì vận tốc chèo lớn hơn vận tốc bè là 4km nên x - y = 4 (1)

Thời gian chèo : $\frac{10}{x} 3 h 20' = \frac{10}{3}$

Thời gian bè trôi: $\frac{10}{y} \Rightarrow \frac{10}{y} - \frac{10}{x} = \frac{10}{3} \Rightarrow \frac{1}{y} - \frac{1}{x} = \frac{1}{3} (2)$

Từ (1) và (2) $\Rightarrow \{\begin{cases} x = y + 4 \\ \frac{1}{y} - \frac{1}{x} = \frac{1}{3} \end{cases} \Leftrightarrow [\begin{array}{l} \{\begin{cases} x = 6 \\ y = 2 \end{cases} (t m) \\ \{\begin{cases} x = - 2 \\ y = - 6 \end{cases} (k t m) \end{array}$

Vậy vận tốc bè gỗ là 2 km/h.

Câu 4:

Hai vòi nước cùng chảy vào 1 bể thì sau 4 giờ 48 phút bể đầy. Nếu vòi I chảy trong 4 giờ, vòi II chảy trong 3 giờ thì cả hai vòi chảy được $\frac{3}{4}$ bể. Tính thời gian mỗi vòi chảy một mình đầy bể

Gọi x (giờ) là thời gian chảy đầy của vòi I

y (giờ) là thời gian chảy đầy của vòi II (x > 4,8; y > 4,8)

$4 h 48' = \frac{24}{5} \Rightarrow$ Trong 1 giờ 2 vòi chảy được : $\frac{1}{x} + \frac{1}{y} = \frac{5}{24} (1)$

Vòi I chảy 4h, vòi II chảy 3 giờ được $\frac{3}{4}$ bể nên $\frac{4}{x} + \frac{3}{y} = \frac{3}{4} (2)$

Từ (1), (2) ta có hệ phương trình $\{\begin{cases} \frac{1}{x} + \frac{1}{y} = \frac{5}{24} \\ \frac{4}{x} + \frac{3}{y} = \frac{3}{4} \end{cases} \Leftrightarrow \{\begin{cases} x = 8 \\ y = 12 \end{cases} (t m)$

Vậy, vòi I: 8 giờ, vòi II: 12 giờ.

Câu 5:

Một tam giác có chiều cao bằng $\frac{3}{4}$ cạnh đáy. Nếu chiều cao tăng thêm 3dm và cạnh đáy giảm đi 3dm thì diện tích của nó tăng thêm $12 d m^{2} .$ Tính chiều cao và cạnh đáy của tam giác.

Gọi x (dm) là chiều cao, y (dm) là cạnh đáy (y > x > 0, y > 3)

Vì chiều cao $= \frac{3}{4}$ cạnh đáy $\Rightarrow x - \frac{3}{4} y = 0 (1)$

Nếu tăng chiều cao thêm 3dm, giảm đáy 3dm thì diện tích tăng $12 d m^{2}$

$\Rightarrow \frac{(x + 3) (y - 3)}{2} - \frac{x y}{2} = 12 \Leftrightarrow x y + 3 y - 3 x - 9 - x y = 24 \Leftrightarrow x - y = - 11 (2)$

Từ (1), (2) suy ra $\{\begin{cases} x - \frac{3}{4} y = 0 \\ x - y = 11 \end{cases} \Leftrightarrow \{\begin{cases} x = 33 \\ y = 44 \end{cases} (t m)$

Vậy chiều cao: 33dm, cạnh đáy: 44dm

Câu 6:

Một khu vườn hình chữ nhật có chu vi bằng 48m. Nếu tăng chiều dài lên 4 lần và chiều rộng lên 3 lần thì chu vi của khu vườn sẽ là 162m. Hãy tìm diện tích của khu vườn ban đầu.

Gọi x (m) là chiều dài, y (m) là chiều rộng (0 < y < x < 24)

Vì chu vi là 48m $\Rightarrow x + y = 24 (1)$

Tăng chiều dài 4 lần, chiều rộng 3 lần được chu vi $162 m \Rightarrow 4 x + 3 y = 81 (2)$

Từ (1), (2) ta có hệ $\{\begin{cases} x + y = 24 \\ 4 x + 3 y = 81 \end{cases} \Leftrightarrow \{\begin{cases} x = 9 \\ y = 15 \end{cases} (t m)$

Vậy diện tích ban đầu: $15.9 = 135 (m^{2})$

Câu 7:

Tìm số tự nhiên có 2 chữ số, biết rằng chữ số hàng đơn vị lớn hơn chữ số hàng chục là 3 đơn vị, nếu viết thêm chữ số 1 vào giữa chữ số hàng chục và hàng đơn vị thì số đó tăng thêm 460 đơn vị.

Gọi a là chữ số hàng chục, b là chữ số hàng đơn vị $(a, b \in ℕ, 3 < a < b < 10)$

Vì hàng đơn vị hơn hàng chục 3 đơn vị nên -a + b = 3 (1)

Nếu viết 1 vào giữa hai số được số mới tăng $460 \Rightarrow \bar{a 1 b} - \bar{a b} = 460$

$\Leftrightarrow 100 a + 10 b - 10 b - b = 5 = 460 \Leftrightarrow a = 5 \Rightarrow b = 8 (t m)$

Vậy số cần tìm là 58.

Câu 8:

Trong hội trường có một số băng ghế, mỗi băng ghế quy định ngồi một số người như nhau. Nếu bớt 2 băng ghế và mỗi băng ghế ngồi thêm 1 người thì thêm được 8 người. Nếu thêm 3 băng ghế và mỗi băng ghế bớt 1 người thì giảm 8 chỗ. Tính số băng ghế trong hội trường.

Gọi x (ghế) là số ghế 1 hàng $(x, y \in ℕ *)$ , y là số hàng

Theo bài ta có hệ phương trình:

$\{\begin{cases} (y - 2) (x + 1) = x y + 8 \\ (y + 3) (x - 1) = x y + 8 \end{cases} \Leftrightarrow \{\begin{cases} - 2 x + y = 10 \\ 3 x - y = 11 \end{cases} \Leftrightarrow \{\begin{cases} x = 21 \\ y = 52 \end{cases}$ (tm)

Vây có 52 băng ghế.

Câu 9:

Trong một kỳ thi, hai trường A, B có tổng cộng 350 học sinh dự thi. Kết quả hai trường đó có 338 học sinh trúng tuyển, tính ra thì trường A có 97% và trường B có 96% số học sinh trúng tuyển. Hỏi mỗi trường có bao nhiêu học sinh dự thi

Gọi x, y lần lượt là số thí sin trường A, B $(x, y \in ℕ *, 0 < x < y < 350)$

Vì tổng có 350 học sinh nên x + y = 350 (1)

Số học sinh trúng tuyển : $338 \Rightarrow 0, 97 x + 0, 96 y = 338 (2)$

Từ (1) và (2) ta có hệ $\{\begin{cases} x + y = 350 \\ 0, 97 x + 0, 96 y = 338 \end{cases} \Leftrightarrow \{\begin{cases} x = 200 \\ y = 150 \end{cases} (t m)$

Vậy trường A: 200 em, trường B: 150 em.

Câu 10:

Một chiếc thuyền xuôi, ngược trên khúc sông dài 40km hết 4 giờ 30 phút. Cho biết thời gian thuyền xuôi dòng 5km bằng thời gian ngược dòng 4km. Hãy tính vận tốc dòng nước.

Gọi x là vận tốc ca nô thực , y là vận tốc nước (x > y > 0)

Tổng thời gian đi và về: $4 h 30' = \frac{9}{2} h$

Thời gian xuôi: $\frac{5}{x + y};$ thời gian ngược: $\frac{4}{x - y} \Rightarrow \frac{5}{x + y} - \frac{4}{x - y} = 0 (1)$

Thời gian xuôi: $\frac{40}{x + y};$ thời gian ngược: $\frac{40}{x - y}$ $\Rightarrow \frac{40}{x + y} + \frac{40}{x - y} = \frac{9}{2} (2)$

Từ (1), (2) $\Rightarrow \{\begin{cases} \frac{5}{x + y} - \frac{4}{x - y} = 0 \\ \frac{40}{x + y} + \frac{40}{x - y} = \frac{9}{2} \end{cases} \Leftrightarrow \{\begin{cases} \frac{1}{x + y} = \frac{1}{20} \\ \frac{1}{x - y} = \frac{1}{16} \end{cases} \Leftrightarrow \{\begin{cases} x = 18 \\ y = 2 \end{cases} (t m)$

Vậy vận tốc nước là 2 km/h

Câu 11:

Cho hai vòi chảy nước cùng 1 lúc vào 1 cái bể cạn thì sau 12 giờ sẽ đầy bể. Nếu cho vòi nước I chảy trong 4 giờ rồi khóa vòi I lại, cho vòi II chảy tiếp trong 6 giờ nữa thì được $\frac{2}{5}$ bể. Tính thời gian mỗi vòi chảy riêng để đầy bể.

Gọi x, y lần lượt là thời gian vòi I, II chảy đầy bể (x, y > 12)

Vì chảy 12 giờ đầy bể nên $\frac{1}{x} + \frac{1}{y} = \frac{1}{12} (1)$

Vòi I chảy 4 giờ, vòi II chảy 6 giờ được $\frac{2}{5}$ bể nên $\frac{4}{x} + \frac{6}{y} = \frac{2}{5} (2)$

Từ (1), (2) ta có hệ $\{\begin{cases} \frac{1}{x} + \frac{1}{y} = \frac{1}{12} \\ \frac{4}{x} + \frac{6}{y} = \frac{2}{5} \end{cases} \Leftrightarrow \{\begin{cases} x = 20 \\ y = 30 \end{cases} (t m)$

Vậy vòi I: 20 giờ , vòi II: 30 giờ.

Câu 12:

Từ một điểm M cố định ở bên ngoài đường tròn (O), ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn. Chứng minh $M T^{2} = M A . M B$

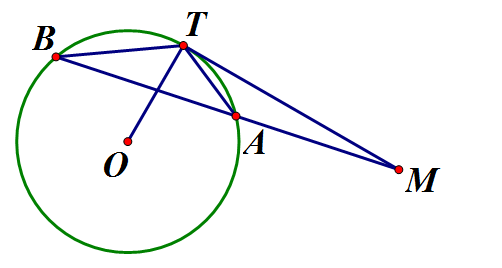
Từ một điểm M cố định ở bên ngoài đường tròn (O), ta kẻ một tiếp tuyến MT (ảnh 1)

Xét

Δ B T M

và

Δ T A M

có:

∠ B = ∠ T, ∠ M \Rightarrow Δ B T M ~ Δ T A M (g . g)

\Rightarrow \frac{M T}{M B} = \frac{M A}{M T} \Rightarrow M T^{2} = M A . M B

Câu 13:

Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại A cắt BC ở I

a) Chứng minh : $\frac{I B}{I C} = \frac{A B^{2}}{A C^{2}}$

b) Tính IA, IC biết rằng $A B = 20 c m, A C = 28 c m, B C = 24 c m$

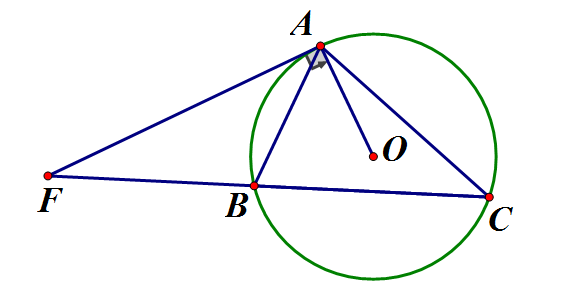
Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại A cắt BC ở I a) Chứng minh (ảnh 1)

a) Ta có: $∠ B A I = ∠ C, ∠ I c h u n g \Rightarrow Δ B A I ~ Δ A C I (g . g)$

$\Rightarrow \frac{A B}{A C} = \frac{I B}{I C} \Rightarrow \frac{A B^{2}}{A C^{2}} = \frac{I B^{2}}{I A^{2}}$

Ta lại có : $I A^{2} = I B . I C \Rightarrow \frac{A B^{2}}{A C^{2}} = \frac{I B}{I C}$

b) Đặt IA = x, IC = y. Ta có: $Δ B A I ~ Δ A C I (g . g)$

$\Rightarrow \frac{A I}{C I} = \frac{B I}{A I} = \frac{A B}{C A} \Rightarrow \frac{x}{y} = \frac{y - 24}{x} = \frac{20}{28} = \frac{5}{7} \Rightarrow \{\begin{cases} x = 35 \\ y = 49 \end{cases}$

Câu 14:

Cho tam giác ABC nội tiếp (O). Tiếp tuyến tại A của (O) cắt BC tại P

a) Chứng minh $Δ P A C ~ Δ P B A$

b) Chứng minh : $P A^{2} = P B . P C$

c) Tia phân giác trong của góc $∠ A$ cắt BC và (O) lần lượt tại D và M. Chứng minh $M B^{2} = M A . M D$

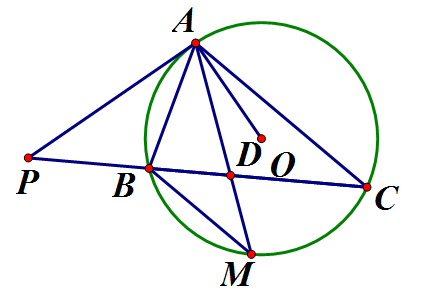
Cho tam giác ABC nội tiếp (O). Tiếp tuyến tại A của (O) cắt BC tại P a) Chứng minh (ảnh 1)

$∠ P A C = ∠ A B P$ (tính chất tiếp tuyến); $∠ P$ chung $\Rightarrow Δ P A C ~ Δ P B A (g - g)$

$Δ P A C ~ Δ P B A (c m t) \Rightarrow \frac{P A}{P B} = \frac{P C}{P A} \Rightarrow P A^{2} = P B . P C$

$∠ B A M = ∠ C A M$ (phân giác) $\Rightarrow ∠ C A M = ∠ C B M \Rightarrow ∠ B A M = ∠ D B M$ và $∠ M$ chung nên $Δ A B M ~ Δ B D M \Rightarrow \frac{M A}{D M} = \frac{M A}{M B} \Rightarrow M B^{2} = M A . M D$

Câu 15:

Cho tam giác ABC nội tiếp đường tròn (O) và AB < AC. Đường tròn (O) đi qua B và C, tiếp xúc với AB tại B cắt đường thẳng AC tại D. Chứng minh $O A ⊥ B D$

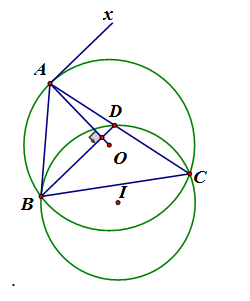
Cho tam giác ABC nội tiếp đường tròn (O) và AB < AC. Đường tròn (O) (ảnh 1)

Vẽ tiếp tuyến Ax của (O), có:

$∠ x A B = \frac{1}{2} s d \overset{⏜}{A B}$ (tiếp tuyến dây cung); $∠ A C B = \frac{1}{2} s d \overset{⏜}{A B}$ (góc nội tiếp) nên $∠ x A B = ∠ A C B (1)$ , có: $∠ A B D$ và $∠ A C B > ∠ x A C$

$A x / / B y \{\begin{cases} ∠ A B D = \frac{1}{2} s d \overset{⏜}{B C} \\ ∠ A C B = \frac{1}{2} s d \overset{⏜}{B D} \end{cases} \Rightarrow ∠ A B D = ∠ A C B (2)$

Từ (1) và (2) suy ra $∠ x A B = ∠ A B D \Rightarrow A x / / B D$ mà $O A ⊥ A x \Rightarrow O A ⊥ B D$

Câu 16:

Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Từ A vẽ hai tiếp tuyến với hai đường tròn, Hai tiếp tuyến này gặp (O) ở C và gặp (O') ở D. Chứng minh rằng $∠ C B A = ∠ D B A$

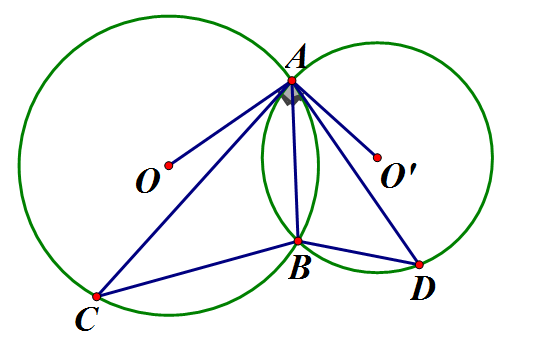
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Từ A vẽ hai tiếp tuyến với (ảnh 1)

Δ A B C, Δ P B A

có

∠ A_{1} = ∠ D, ∠ C = ∠ B A D

(cùng chắn cung AB)

\Rightarrow Δ A B C ~ Δ D B A (g . g) \Rightarrow ∠ C B A = ∠ D B A

Câu 17:

Tam giác đều ABC nội tiếp đường tròn (O). Vẽ một đường tròn (O') tiếp xúc trong với đường tròn (O) tại điểm T trên cung nhỏ AB và cắt các dây TA, TB, TC lần lượt tại D, E, F. Chứng minh rằng:

$\begin{array}{l} a) E F / / B C, D F / / A C, D E / / A B \\ b) T C = T A + T B \end{array}$

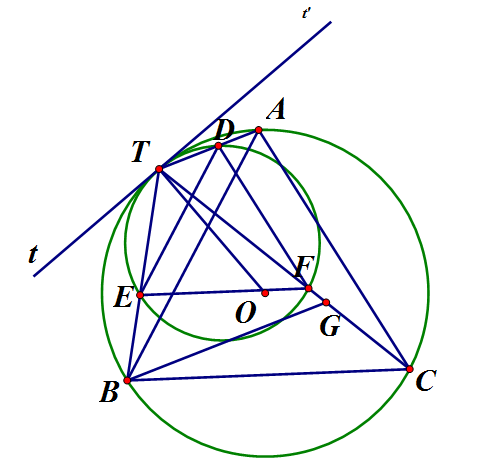
Tam giác đều ABC nội tiếp đường tròn (O). Vẽ một đường tròn (O') tiếp xúc trong (ảnh 1)

Qua T vẽ tiếp tuyến chung tTt'với hai đường tròn

Ta có: $∠ B T t = ∠ E F T$ (tiếp tuyến – dây cung)

Tương tự: $∠ B T t = ∠ B C T \Rightarrow ∠ E F T = ∠ B C T \Rightarrow E F / / B C$

Chứng minh tương tự : $D F / / A C, D E / / A B$

Lấy G thuộc tia TC sao cho TG = TB

$Δ T B G$ cân (TG = TB) và $∠ B T G = 60^{0} \Rightarrow Δ T B G$ đều $\Rightarrow ∠ B G T = 60^{0}$

Xét $Δ A T B, Δ C G B$ có: $∠ T A B = ∠ T C B$ (cùng chắn $\overset{⏜}{T B}), A B = B C (g t), ∠ T B A = ∠ G B C$

Do đó: $Δ A T B = Δ C G B (g . c . g) \Rightarrow T A = G C$ mà $T G + G C = T C = T A + T B$ (đpcm)

Câu 18:

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài nhau tại P. Từ một điểm A của (O) kẻ hai tiếp tuyến (O') với (O) cắt AP tại C. Tia AP cắt (O') tại D.

Chứng minh : $∠ C P B = ∠ B P D$

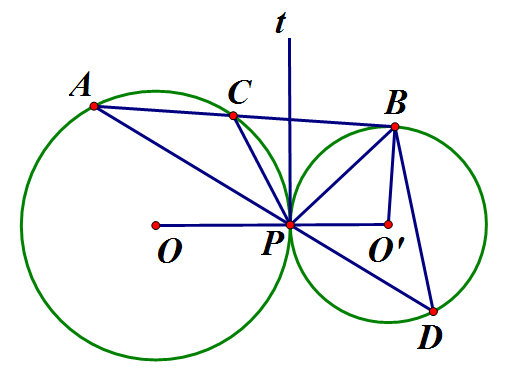
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài nhau tại P. Từ một điểm A (ảnh 1)

Vẽ tiếp tuyến chung Pt của đường tròn (O) và (O'). Ta có: $∠ C P t = ∠ A C P$

Mà $∠ C B P = ∠ B P t$ (cùng chắn cung PB của (O))

$\Rightarrow ∠ C P t + ∠ B P t = ∠ C A P + ∠ C B P$ hay $∠ C P B = ∠ C A P + ∠ C B P$

Mặt khác $Δ A B P$ có $∠ B P D$ là góc ngoài $\Rightarrow ∠ B P D = ∠ C A P + ∠ C B P$

Vậy $∠ C P B = ∠ B P D$

Bắt đầu thi ngay

Có thể bạn quan tâm

Các bài thi hot trong chương