Dạng 6: Trắc nghiệm Hình học có đáp án
-
1184 lượt thi
-
13 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hình vuông ABCD. Gọi là diện tích phần giao của hai nửa đường tròn đường kính AB và AD. là diện tích phần còn lại của hình vuông nằm ngoài hai nửa đường trong nói trên (như hình vẽ bên).Tính
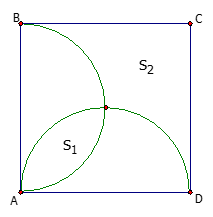
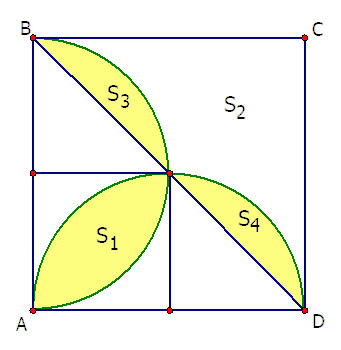
Gọi a là cạnh hình vuông ABCD. Ta cm được:
Câu 2:
Áp dụng Pitago vào tam giác vuông
.
Áp dụng hệ thức lượng vào tam giác vuông ABC
Do đó
Áp dụng Pitago vào tam giác vuông ABC
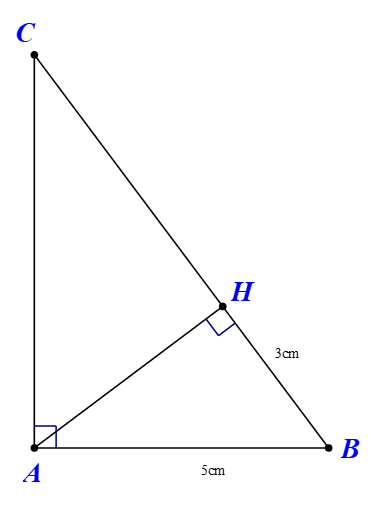
Câu 3:
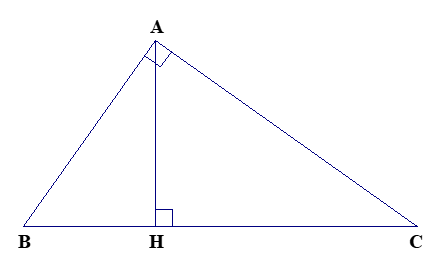
Áp dụng hệ thức lượng vào tam giác ABC vuông tại A, đường cao ta có:
Câu 4:
a) Chứng minh . Từ đó suy ra tứ giác nội tiếp.
b) Chứng minh song song với .
c) Tìm hệ thức liên hệ giữa sđ và sđ để song song với .
Câu 5:
Cho đường tròn (O; R) có đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn (O; R) sao cho đoạn thẳng AC cắt đường tròn (O; R) tại điểm K (K khác A), hai dây MN và BK cắt nhau ở E.
a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.
b) Chứng minh: CA.CK = CE.CH.
c) Qua điểm N, kẻ đường thẳng (d) vuông góc với AC, (d) cắt tia MK tại F. Chứng minh tam giác cân.
d) Khi KE = KC. Chứng minh rằng: OK // MN.
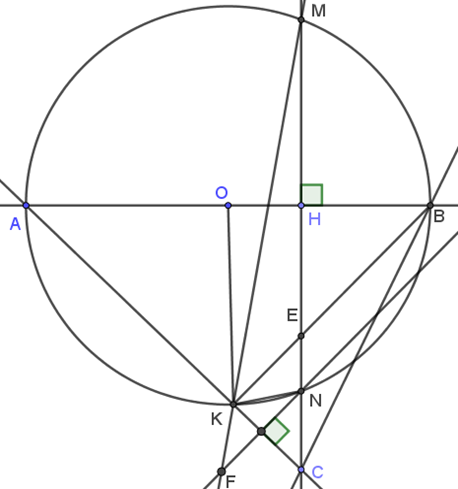
a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.
Ta có :
(1)
Hai góc đối nhau (2)
Từ (1), (2) ta có tứ giác AHEK nội tiếp đường tròn đường kính AE.
b) Chứng minh: CA.CK = CE.CH.
Do tứ giác AHEK nội tiếp nên
vì chung và
nên
c)Qua điểm N, kẻ đường thẳng (d) vuông góc với AC, (d) cắt tia MK tại F. Chứng minh tam giác cân.
Do KB // FN nên (3)
mà (góc nội tiếp cùng chắn cung bằng nhau) (4)
(3), (4) nên tam giác KFN cân tại K.
d) Khi KE = KC. Chứng minh rằng: OK // MN.
Ta có vuông tại K.
mà KE = KC nên tam giác KEC vuông cân tại K
hay
mà nên OK //MN
Câu 6:
Nhằm tiếp tục đẩy mạnh phong trào xây dựng trường học Xanh-Sạch-Đẹp, trường THCS A đã thiết kế một khuôn viên để trồng hoa có dạng hình tam giác vuông (như hình bên). Biết rằng tam giác MNK vuông tại M , MN=6m, MK=8m, MH vông góc với NK , MN=6m, MK=8 m, MH vuống góc NK . Nhà trường trồng hoa mười giờ dọc theo các đoạn NK , MH.
Tính độ dài các đoạn NK, MH. Biết chi phí trồng hoa mười giờ là đồng trên mỗi mét chiều dài. Tính tổng chi phí để trồng các luống hoa mười giờ đó.
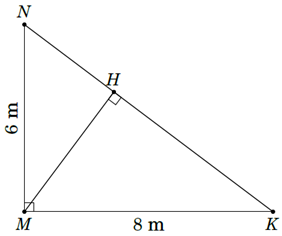
Tam giác vuông tại M nên m.
Lại có nên m.
Tổng chiều dài NK và là m.
Tổng chi phí để trồng các luống hoa mười giờ đó là đồng.
Câu 7:
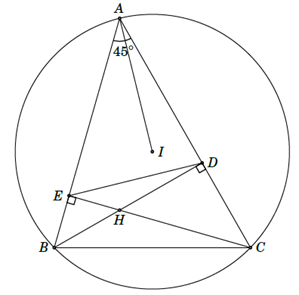
a) Theo giả thiết . Khi đó tứ giác có đỉnh E và D cùng nhìn cạnh dưới hai góc bằng nhau nên tứ giác nội tiếp.
b) Tứ giác nội tiếp nên (cùng bù với ).
Xét và có và chung nên .
Do đó .
Từ .
Vì vuông tại D nên ta có
.
c) vuông tại D và nên
vuông cân tại E . (1)
Chứng minh tương tự vuông cân tại D . (2)
Từ (1) và (2) suy ra .
d) Vì I là tâm đường tròn ngoại tiếp tam giác ABC nên I là giao điểm của ba đường trung trực của tam giác ABC .
Ta có thuộc trung trực của ; E thuộc trung trực của AC (vì tam giác AEC vuông cân tại E) suy ra . (3)
Chứng minh tương tự . (4)
Từ (3) và (4) suy ra là trực tâm của .
Câu 8:
a) Chứng minh tứ giác AHCE là tứ giác nội tiếp
b) Chứng minh
c) Chứng minh tam giác EHC cân
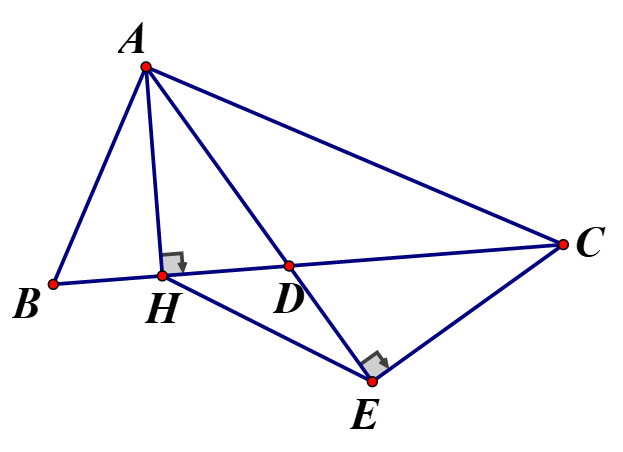
Ta có: mà H, E là hai đỉnh kề nhau cùng nhìn AC
Suy ra tú giác AHEC nội tiếp
b. Xét và có:
( đối đỉnh)
( cùng nhìn EC trong tứ giác nội tiếp AHEC)
\
c. Ta có: BA=BD (gt) suy ra tam giác ABD cân tại B
Mà ( đối đỉnh)
Mà (cùng nhìn cung EC)
cân tại E
Câu 9:
Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn đó. Kẻ cát tuyến AMN không đi qua (O) (M nằm giữa A và N). Kẻ hai tiếp tuyến AB, AC với (O;R). (B và C là hai tiếp điểm và C tuộc cung nhỏ MN). Đường thẳng BC cắt MN và AO lần lượt tại E và F. Gọi I là trung điểm của MN.
a) Chứng minh rằng tứ giác ABOC nội tiếp được trong đường tròn.
b) Chứng minh EB.EC = EM.EN và IA là phân giác của .
c) Tia MF cắt (O;R) tại điểm thứ hai là D. Chứng minh rằng và .
d) Giả sử OA = 2R. Tính diện tích tam giác ABC theo R.
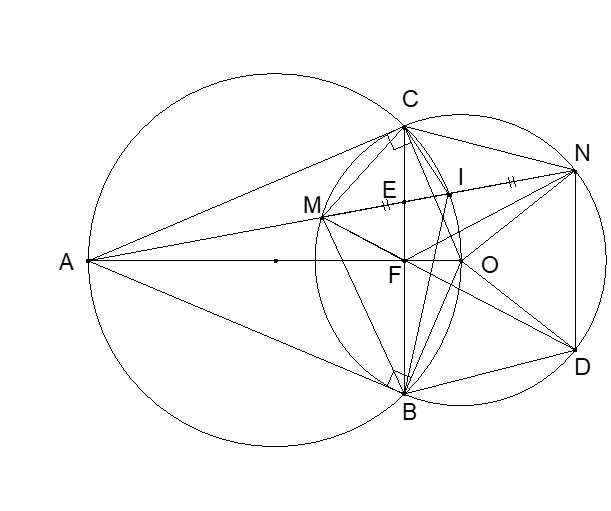
a) Vì AB là tiếp tuyến của (O) tại tiếp điểm B AB OB hay
Vì AC là tiếp tuyến của (O) tại tiếp điểm C AC OC hay .
Tứ giác ABOC có nên tứ giác ABOC nội tiếp đường tròn đường kính AO.
b) Xét và có:
(hai góc nội tiếp cùng chắn cung NB)
(hai góc nội tiếp cùng chắn cung MC)
.
Vì AB, AC là tiếp tuyến của (O) lần lượt tại các tiếp điểm B và C nên và AB = AC (tính chất hai tiếp tuyến cắt nhau)
Vì I là trung điểm MN (quan hệ vuông góc giữa đường kính và dây)
I nằm trên đường tròn đường kính OA.
Xét đường tròn đường kính OA ta có:
(hai góc nội tiếp cùng chắn một cung)
Mà
hay IA là phân giác của .
d) Xét vuông tại C ta có:
.
Xét vuông tại C ta có:
có AB = AC và suy ra là tam giác đều.
đường cao
Câu 10:
Cho điểm S cố định ở bên ngoài đường tròn (O). Vẽ tiếp tuyến SA của đường tròn (O) (với A là tiếp điểm) và cát tuyến SCB không qua tâm O, điểm O nằm trong góc ASB, điểm C nằm giữa S và B. Gọi H là trung điểm của đoạn thẳng CB.
a) Chứng minh rằng tứ giác SAOH nội tiếp một đường tròn
b) Chứng mnh rằng
c) Gọi MN là đường kính bất kỳ của đường tròn (O) sao cho ba điểm S, M, N không thẳng hàng. Xác định vị trí của MN để diện tích tam giác SMN lớn nhất
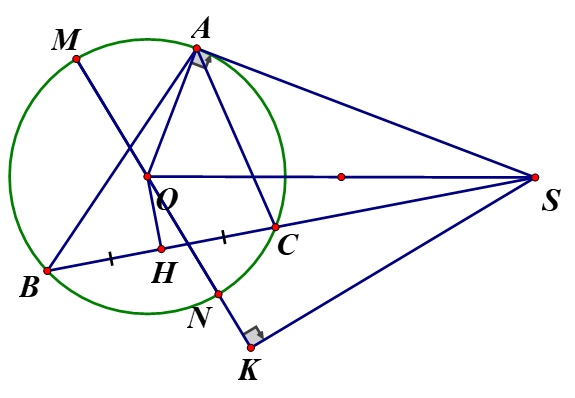
a) Vì H là trung điểm của BC
Tứ giác OASH có : là tứ giác nội tiếp
b) Xét và có : chung; (cùng chắn cung AC)
(g.g)
c) Kẻ
Ta có (vì vuông tại O )
Vậy để lớn nhất thì
vừa là đường trung tuyến, vừa là đường cao
cân tại S
Câu 11:
Kim tự tháp Keop – Ai cập có dạng hình chóp đều, đáy là hình vuông, các mặt bên là các tam giác cân chung đỉnh. Mỗi cạnh bên của kim tự tháp dài 214m, cạnh đáy của nó dài 230m.
a) Tính theo mét chiều cao h của kim tự tháp (làm tròn đến số thập phân thứ nhất)
b) Cho biết thể tích của hình chóp được tính theo công thức , trong đó S là diện tích mặt đáy, h là chiều cao của hình chóp. Tính theo m3 thể tích của kim tự tháp (làm tròn đến hàng nghìn)
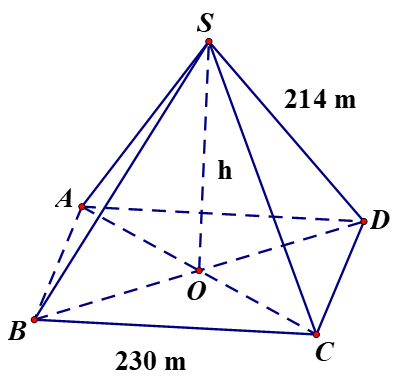
a) Vì ABCD là hình vuông
Tam giác SAO vuông tại O nên áp dụng Pytago ta có:
b) T a có diện tích mặt đáy là:
Thể tích của kim tự tháp là
Câu 13:
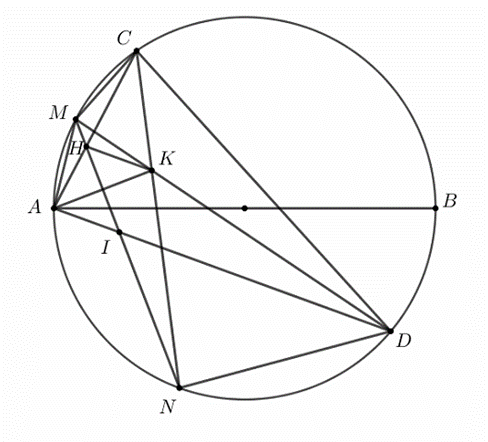
Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O. Tiếp tuyến của đường tròn tâm O tại điểm C cắt các đường thẳng AB và AD theo thứ tự tại M, N. Gọi H là chân đường cao hạ từ A xuống BD, K là giao điểm của hai đường thẳng MN và BD.
a) Chứng minh tứ giác AHCK là tứ giác nội tiếp
b) Chứng minh:
c) Gọi E là trung điểm của MN. Chứng minh ba điểm A, H, E thẳng hàng
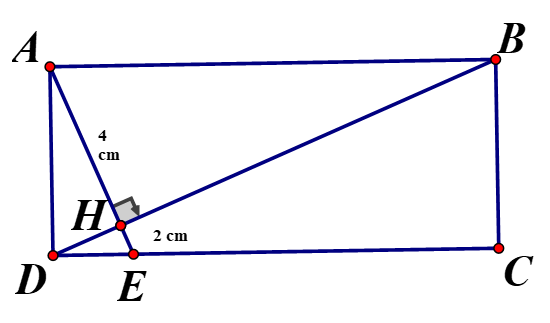
d) Cho AB = 6 cm, AD = 8 cm. Tính độ dài đoạn MN.
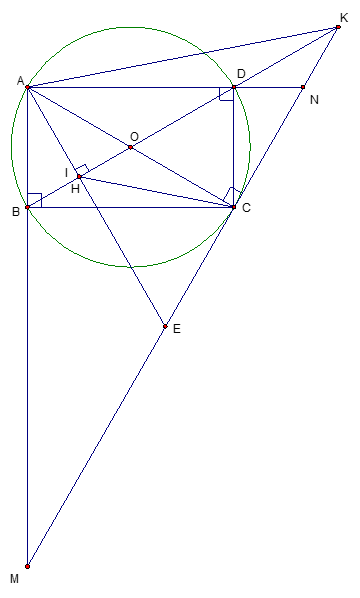
a) Xét tứ giác AHCK có (gt)
CK là tiếp tuyến của đường tròn tâm O, AC là đường kính nên .
Suy ra
Vậy hai đỉnh H và C cùng nhìn AK dưới một góc vuông
nên AHCK là tứ giác nội tiếp.
b) Vì ABCD là hình chữ nhậ nên
(cùng phụ với )
Do đó
Xét và ta có:
(cmt)
Nên (g.g)
Suy ra
c) Gọi E là trung điểm của MN. Chứng minh ba điểm thẳng hàng
Giả sử AE cắt BD tại I, ta chứng minh . Thật vậy:
Tam giác AMN vuông tại A có E là trung điểm MN nên tam giác AEN cân tại E, do đó (3)
Theo chứng minh trên: (4)
Từ (3) và (4) ta có: hay
Suy ra tại I. Do đó hay thẳng hàng.
d) Đặt . Khi đó và:
Mặt khác: .