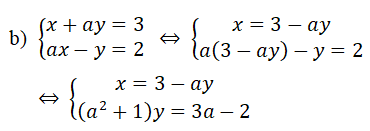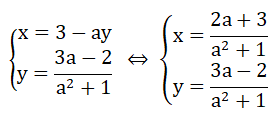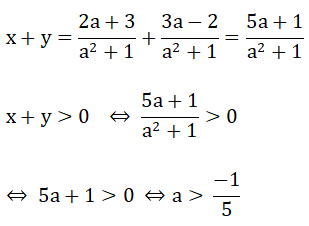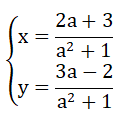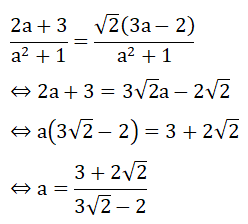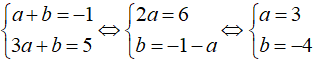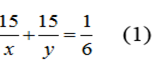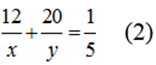11 câu hỏi trắc nghiệm thuộc Đề kiểm tra 1 tiết Toán 9 Chương 3 Đại số có đáp án (Đề 3)

Đề kiểm tra 1 tiết Toán 9 Chương 3 Đại số có đáp án

Đề kiểm tra 1 tiết Toán 9 Chương 3 Đại số có đáp án (Đề 3)

2001 lượt thi
11 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Phần trắc nghiệm

Nội dung câu hỏi 1

Cho phương trình 3x + 4y = 5 . Khẳng định nào sau đây là sai?

A. Phương trình có vô số nghiệm trên R

B. Công thức nghiệm tổng quát của phương trình là: $(x \in ℝ; y = \frac{- 3 x + 5}{4})$

C. Phương trình có cặp nghiệm là cặp số tự nhiên

D. Phương trình không có nghiệm là cặp số nguyên âm.

Xem đáp án

Đáp án là C

Câu 2:

Cho hệ phương trình bậc nhất hai ẩn:

$(I) \{\begin{cases} a x + b y = c \\ a' x + b' y = c' \end{cases}$

Với a, b, c, a’, b’, c’ ≠ 0. Hệ (I) có nghiệm duy nhất khi:

A. $\frac{a}{a'} = \frac{b}{b'} \neq \frac{c}{c'}$

B. $\frac{a}{a'} \neq \frac{b}{b'}$

C. $\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'}$

Xem đáp án

Đáp án là B

Câu 3:

Cho hệ phương trình: $\{\begin{cases} 3 x - 4 y = 7 \\ x - 2 y = 3 \end{cases}$

Nghiệm của hệ là:

A.(1;1)

B.(-1;1)

C.(1;-1)

D.(2;-1)

Xem đáp án

Đáp án là C

Câu 4:

Cho hệ phương trình: $\{\begin{cases} m x - y = m + 2 \\ x + y = 1 \end{cases}$

Giá trị m để hệ có nghiệm duy nhất là:

A. m ≠ -1

B. m = 1

C. m ≠ 3

D. m ≠ -2

Xem đáp án

Đáp án là A

Câu 5:

Phương trình ax + by =c là phương trình bậc nhất hai ẩn, trong đó a, b, c là các số đã biết, với:

A. a ≠ 0 hoặc b ≠ 0 và x, y là các ẩn

B. a, b là các số nguyên, a ≠ 0; b ≠ 0 và x, y là các ẩn

C. $a^{2} + b^{2}$ = 0 và x, y là các ẩn

D. $a^{2} + b^{2}$ = 0;x ≠ 0;y ≠ 0

Xem đáp án

Đáp án là A

Câu 6:

Cho hệ phương trình: $\{\begin{cases} m x + y = - 3 \\ 3 x - 2 y = 6 \end{cases}$

Giá trị m để hệ phương trình có vô số nghiệm là:

A. m = 1

B. m = -3

C. m = 2

D. m = -3/2

Xem đáp án

Đáp án là D

Câu 7:

Phần tự luận

Nội dung câu hỏi 1

Cho hệ phương trình : $\{\begin{cases} x + a y = 3 \\ a x - y = 2 \end{cases}$

a) Giải hệ phương trình khi a = 2

Xem đáp án

a) Khi a = 2, ta có hệ phương trình

Vậy hệ phương trình có nghiệm duy nhất (x; y) = (7/5; 4/5)

Câu 8:

Cho hệ phương trình :

$\{\begin{cases} x + a y = 3 \\ a x - y = 2 \end{cases}$

b) Tìm điều kiện của a để hệ phương trình có nghiệm duy nhất thỏa mãn x + y > 0

Xem đáp án

Do $a^{2}$ + 1 ≠ 0 ∀ x nên hệ phương trình trở thành:

Khi đó:

Vậy với a > (-1)/5 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x+y >0

Câu 9:

Cho hệ phương trình : $\{\begin{cases} x + a y = 3 \\ a x - y = 2 \end{cases}$

c) Tìm giá trị của a để hệ phương trình có nghiệm (x; y) thỏa mãn x = $\sqrt{2}$ y

Xem đáp án

c) Hệ phương trình đã cho có nghiệm

Theo đề bài : x= $\sqrt{y}$

Vậy với thì hệ phương trình có nghiệm (x; y) thỏa mãn x = $\sqrt{2}$ y

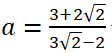
Câu 10:

Lập phương trình đường thẳng đi qua hai điểm (1; -1) và (3; 5)

Xem đáp án

Phương trình đường thẳng cần tìm có dạng: y = ax + b

Đường thẳng đi qua điểm (1; -1) nên ta có: a + b = -1

Đường thẳng đi qua điểm (3; 5) nên ta có: 3a + b = 5

Khi đó ta có hệ phương trình

Vậy phương trình đường thẳng cần tìm là y = 3x – 4.

Câu 11:

Hai người cùng làm chung trong 15 giờ thì được 1/6 công việc. Nếu để người thứ nhất làm một mình trong 12 giờ, người thứ hai làm trong 20 giờ thì cả hai làm được 1/5 công việc. Hỏi nếu để mỗi người làm riêng thì xong công việc trong bao lâu?

Xem đáp án

Gọi thời gian người thứ nhất làm riêng xong công việc là x(giờ)

Gọi thời gian người thứ hai làm riêng xong công việc là y(giờ)

Điều kiện: x; y > 0

Trong 1 giờ người thứ nhất làm được 1/x (công việc)

Trong 1 giờ người thứ hai làm được 1/y (công việc)

Vì hai người làm chung trong 15 giờ được 1/6 công việc nên ta có phương trình: