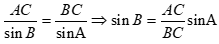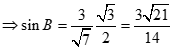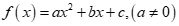Đề kiểm tra giữa học kì 2 Toán 10 có đáp án (Mới nhất) (Đề 3)
-
1436 lượt thi
-
38 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
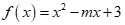 . Với giá trị nào của m thì f(x) có hai nghiệm phân biệt?
. Với giá trị nào của m thì f(x) có hai nghiệm phân biệt?Chọn đáp án A
Để f(x) có hai nghiệm phân biệt thì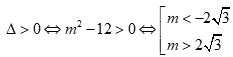
Câu 2:
Tìm tất cả các giá trị thỏa mãn điều kiện của bất phương trình ![]()
Chọn đáp án D
Điều kiện: 2- x > 0
Vậy
Câu 3:
Cặp bất phương trình nào sau đây là tương đương?
Chọn đáp án B
Bất phương trình![]()
Bất phương trình 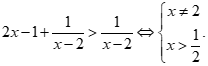 Đáp án A sai.
Đáp án A sai.
Bất phương trình 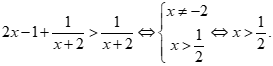 Đáp án B đúng.
Đáp án B đúng.
Bất phương trình 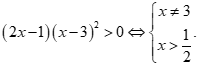 Đáp án C sai.
Đáp án C sai.
Bất phương trình 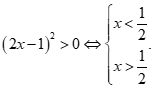 Đáp án D sai.
Đáp án D sai.
Ghi nhớ: Hai bất phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.
Câu 4:
Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
Chọn đáp án C
Ghi nhớ: Bất phương trình bậc nhất một ẩn x có dạng tổng quát là: 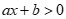 ;
; ![]() ;
; ![]() ;
; ![]() . Trong đó, a, b là các hằng số,
. Trong đó, a, b là các hằng số, ![]() và x là ẩn số.
và x là ẩn số.
Câu 5:
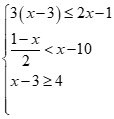 có tập nghiệm là
có tập nghiệm làChọn đáp án C
Ta có 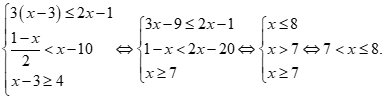
Vậy tập nghiệm của hệ bất phương trình ![]()
Câu 6:
Bảng xét dấu sau là của biểu thức nào?

Chọn đáp án C
* Ta có:
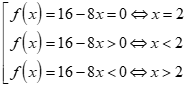
* Hoặc nhận dạng bảng xét dấu của nhị thức bậc nhất “phải cùng trái khác với a”.
Câu 7:
Tập nghiệm của bất phương trình ![]() là:
là:
Chọn đáp án A
![]()
![]()
Vậy tập nghiệm của bất phương trình là ![]()
Câu 8:
Chọn đáp án C
* Với a > 0 ta có: ![]() (không thỏa mãn yêu cầu bài toán là
(không thỏa mãn yêu cầu bài toán là ![]() )
)
* Với a < 0 ta có: ![]() (không thỏa mãn yêu cầu bài toán là
(không thỏa mãn yêu cầu bài toán là ![]() )
)
* Với a = 0 ta có ![]() khi đó
khi đó ![]()
Vậy ![]()
Câu 9:
Chọn đáp án C.
*) Nếu ![]() ta được bất phương trình (1) trở thành
ta được bất phương trình (1) trở thành ![Tìm số các giá trị nguyên của m để mọi x thuộc đoạn [-1; 2] đều là nghiệm của bất phương trình (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2022/06/anh54-1656323504.png) , bất phương trình này đúng với mọi x thuộc
, bất phương trình này đúng với mọi x thuộc ![]()
*) Nếu ![]() ta được bất phương trình (1) có tập nghiệm
ta được bất phương trình (1) có tập nghiệm ![Tìm số các giá trị nguyên của m để mọi x thuộc đoạn [-1; 2] đều là nghiệm của bất phương trình (ảnh 7)](https://video.vietjack.com/upload2/quiz_source1/2022/06/anh57-1656323542.png) khi đó yêu cầu bài toán xảy ra khi
khi đó yêu cầu bài toán xảy ra khi ![]() . Kết hợp với
. Kết hợp với ![Tìm số các giá trị nguyên của m để mọi x thuộc đoạn [-1; 2] đều là nghiệm của bất phương trình (ảnh 9)](https://video.vietjack.com/upload2/quiz_source1/2022/06/anh55-1656323572.png) nên
nên ![]()
*) Nếu ![]() ta được bất phương trình (1) có tập nghiệm
ta được bất phương trình (1) có tập nghiệm ![Tìm số các giá trị nguyên của m để mọi x thuộc đoạn [-1; 2] đều là nghiệm của bất phương trình (ảnh 12)](https://video.vietjack.com/upload2/quiz_source1/2022/06/anh61-1656323640.png) khi đó yêu cầu bài toán xảy ra khi
khi đó yêu cầu bài toán xảy ra khi ![]() . Kết hợp với
. Kết hợp với ![]() nên
nên![]()
Kết hợp cả 3 trường hợp ta có: m thuộc đoạn ![]() sẽ thỏa mãn. Do m nguyên nên
sẽ thỏa mãn. Do m nguyên nên ![]()
Câu 10:
Miền nghiệm của bất phương trình 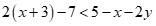 không chứa điểm nào trong các điểm sau?
không chứa điểm nào trong các điểm sau?
Chọn đáp án A
![]()
![]()
![]()
Ta có ![]() , vô lý.
, vô lý.
Vậy miền nghiệm của bất phương trình ![]() không chứa điểm
không chứa điểm ![]()
Câu 11:
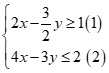 có tập nghiệm là S. Mệnh đề nào sau đây là đúng?
có tập nghiệm là S. Mệnh đề nào sau đây là đúng?Chọn đáp án C
Ta có: 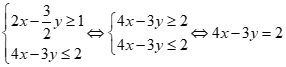
Vậy tập nghiệm của hệ bất phương trình là ![]()
Câu 12:
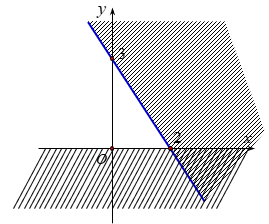
Chọn đáp án B
Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng ![]() và đường thẳng
và đường thẳng![]()
Miền nghiệm gồm phần phía trên trục hoành nên y nhận giá trị dương.
Lại có (0;0) thỏa mãn bất phương trình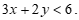
Câu 13:
Chọn đáp án D
Gọi diện tích trồng mía là x (đơn vị: sào, đk: 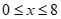 )
)
Gọi diện tích trồng ngô là y (đơn vị: sào, đk: ![]() )
)
Diện tích trồng mía và ngô dự định là 8 sào nên ta có bpt: 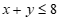
Tổng số công cần dùng cho cả hai loại không vượt quá 90 nên ta có bpt: ![]()
Tổng số tiền lãi thu được là: 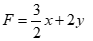 (đơn vị: triệu đồng)
(đơn vị: triệu đồng)
Khi đó, ta đưa về bài toán tìm (x; y) thỏa mãn hbpt: 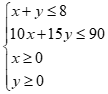 để
để ![]() đạt giá trị lớn nhất.
đạt giá trị lớn nhất.
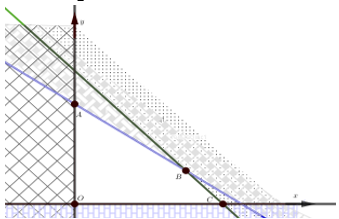
Biểu diễn hình học tập nghiệm hbpt ta được miền nghiệm cuả hbpt là tứ giác OABC kể cả biên,
với 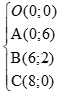
![]()
Câu 14:
Chọn đáp án A
Ta có: 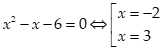
Bảng xét dấu:
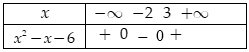
Dựa vào bảng xét dấu ta có: ![]()
Câu 15:
Chọn đáp án C
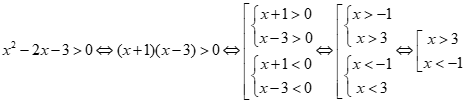
Vậy x < -1 hoặc x>3
Câu 16:
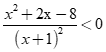 là:
là:Chọn đáp án A
ĐKXĐ: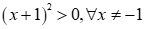 nên bất phương trình đã cho tương đương với
nên bất phương trình đã cho tương đương vớiCâu 17:
Chọn đáp án A
![]()
BXD:

Tập nghiệm của bất phương trình: ![]()
Nghiệm nguyên nhỏ nhất: ![]() ; nghiệm nguyên lớn nhất:
; nghiệm nguyên lớn nhất: ![]()
![]()
Câu 18:
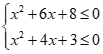 có tất cả bao nhiêu nghiệm nguyên?
có tất cả bao nhiêu nghiệm nguyên?Chọn đáp án C
Ta có 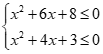
![]()
![]() . Vì
. Vì ![]() nên
nên ![]() . Vậy hệ bất phương trình có hai nghiệm nguyên thoả mãn.
. Vậy hệ bất phương trình có hai nghiệm nguyên thoả mãn.
Câu 19:
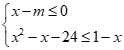 . Hệ đã cho có nghiệm khi và chỉ khi
. Hệ đã cho có nghiệm khi và chỉ khiChọn đáp án D
Hệ tương đương:Câu 23:
Chọn đáp án B
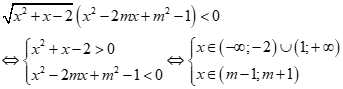
Bất phương trình có nghiệm ![]() (*)
(*)
Ta có ![]()
Câu 24:
Chọn đáp án D
Ta có : 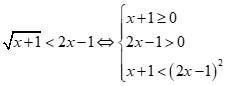
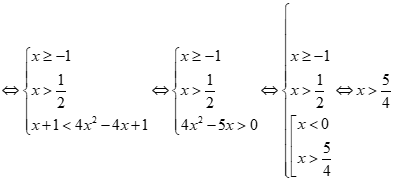 hay
hay ![]()
Ghi nhớ: Công thức được sử dụng:
1) 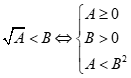 2)
2) 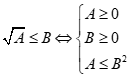
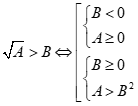 4)
4) 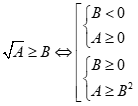
Câu 25:
Chọn đáp án A
Áp dụng định lý cosin trong tam giác, ta cóCâu 26:
Cho ![]() có
có ![]() trên cạnh BC lấy điểm M sao cho
trên cạnh BC lấy điểm M sao cho ![]() .
.
Tính độ dài đoạn AM.
Chọn đáp án D
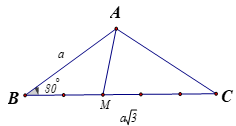
![]()
Áp dụng định lí cô sin cho tam giác ABM ta có:
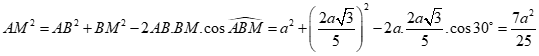
![]()
Câu 27:
Chọn đáp án A
Theo định lí hàm số sin ta có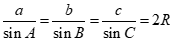
Câu 28:
Muốn đo khoảng cách từ người A trên bờ đến chiếc thuyền C neo đậu trên sông, người ta chọn một điểm B trên bờ và đo được 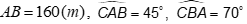 .Tính độ dài đoạn AC (xấp xỉ đến hàng phần trăm)
.Tính độ dài đoạn AC (xấp xỉ đến hàng phần trăm)
Chọn đáp án D
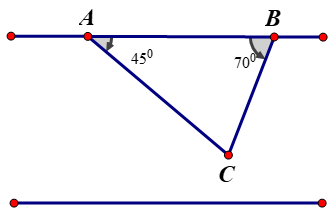
Ta có:
![]()
Áp dụng định lí hàm sin trong ![]() ta có:
ta có:
![]()
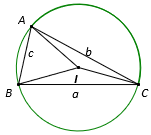
Ghi nhớ: Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.
Câu 29:
Cho tam giác ABC có AB = c, BC = a, AC = b. Gọi M là trung điểm của BC. Mệnh đề nào sau đây đúng?
Chọn đáp án D
Theo công thức tính độ dài đường trung tuyến ta có:
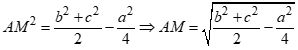
Câu 30:
Chọn đáp án B
Ta có:
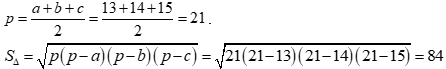
Lại có: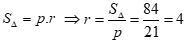
Vậy bán kính đường tròn nội tiếp tam giác r = 4 .
Câu 31:
Chọn đáp án D
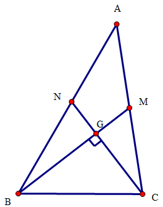
Ta có
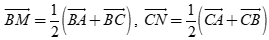
Do các đường trung tuyến BM, CN vuông góc với nhau nên
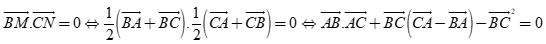
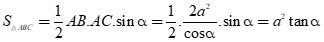
Câu 32:
Cho tam giác ABC có AB = c, AC = b, BC = a. Nhận dạng tam giác ABC biết ![]() .
.
Chọn đáp án A
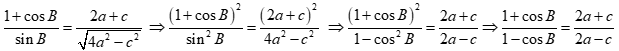
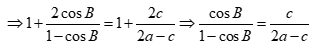
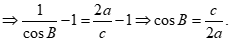
Vậy tam giác ABC cân tại C.
Câu 33:
Tam giác ABC có ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Chọn đáp án D
Áp dụng định lí sin: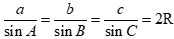
Suy ra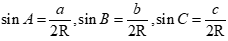
Thay vào biểu thức 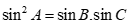 ta được:
ta được:
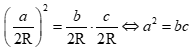
Do đó 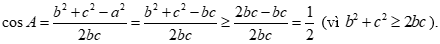
Câu 34:
Chọn đáp án C
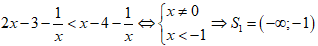
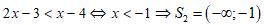
Câu 35:
Bất phương trình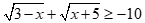 có bao nhiêu nghiệm?
có bao nhiêu nghiệm?
Chọn đáp án B
Điều kiện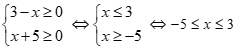
Ta có 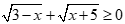 với
với 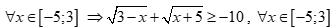
Vậy bất phương trình có vô số nghiệm.
Câu 37:
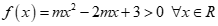
Với m = 0 thì bất phương trình trở thành 3 > 0 luôn đúng với mọi ![]() nên m = 0 thỏa mãn.
nên m = 0 thỏa mãn.
Với thì bất phương trình nghiệm đúng với 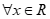 khi và chỉ khi
khi và chỉ khi
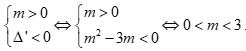
Kết luận: 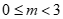 là điều kiện cần tìm.
là điều kiện cần tìm.
Câu 38:
Cho tam giác ABC có ![]() . Tính độ dài BC và sinB .
. Tính độ dài BC và sinB .
Áp dụng định lý cosin ta có
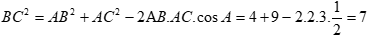
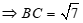
Áp dụng định lý sin ta có