39 câu hỏi trắc nghiệm thuộc Đề kiểm tra giữa học kì 2 Toán 10 có đáp án (Mới nhất) (Đề 10)

Câu 1:

\sqrt{x - 2021} > \sqrt{2021 - x}

là

A. $[2021, + \infty)$ .

B. $(- \infty,2021)$ .

C. $\{2021\}$ .

D. $\emptyset$ .

Xem đáp án

Chọn đáp án D

Điều kiện xác định: $\{\begin{cases} x \geq 2021 \\ x \leq 2021 \end{cases} \Leftrightarrow x = 2021$ .

Thử x = 2021 vào bất phương trình ta có $\sqrt{2021 - 2021} > \sqrt{2021 - 2021} \Leftrightarrow 0 > 0$ ( vô lý). Vậy bất phương trình vô nghiệm.

Câu 2:

Tập nghiệm của bất phương trình

\frac{2 x^{2} - 3 x + 4}{x^{2} + 3} > 2

là

A. $(\frac{3}{4} - \frac{\sqrt{23}}{4}; \frac{3}{4} + \frac{\sqrt{23}}{4})$ .

B. $(- \infty; \frac{3}{4} - \frac{\sqrt{23}}{4}) \cup (\frac{3}{4} + \frac{\sqrt{23}}{4}; + \infty)$ .

C. $(- \frac{2}{3}; + \infty)$ .

D. $(- \infty; - \frac{2}{3})$ .

Xem đáp án

Chọn đáp án D

Do $x^{2} + 3 > 0 \forall x \in ℝ$ nên bất phương trình đã cho tương đương với

$\frac{2 x^{2} - 3 x + 4}{x^{2} + 3} > 2$

$\Leftrightarrow 2 x^{2} - 3 x + 4 > 2 (x^{2} + 3) \Leftrightarrow 3 x < - 2 \Leftrightarrow x < - \frac{2}{3}$

Vậy tập nghiệm của BPT là $S = (- \infty; - \frac{2}{3})$ .

Câu 3:

Cho a là số thực dương. Mệnh đề nào dưới đây đúng?

A. $|x| \geq a \Leftrightarrow - a \leq x \leq a$ .

B. $|x| \leq a \Leftrightarrow x \leq a$ .

C. $|x| > a \Leftrightarrow x > a$ .

D. $|x| \geq a \Leftrightarrow [\begin{array}{l} x \leq - a \\ x \geq a \end{array}$ .

Xem đáp án

Chọn đáp án D

Với a là số thực dương, ta có: $|x| \geq a \Leftrightarrow [\begin{array}{l} x \leq - a \\ x \geq a \end{array}$ .

Câu 4:

Số nghiệm nguyên dương của bất phương trình

(2 - x) (x + 1) (3 - x) \leq 0

là

A. 1.

B. 4.

C. 2.

D. 3.

Xem đáp án

Chọn đáp án C

Ta có:

$2 - x = 0 \Leftrightarrow x = 2 x + 1 = 0 \Leftrightarrow x = - 1 3 - x = 0 \Leftrightarrow x = 3$

Bảng xét dấu vế trái

Số nghiệm nguyên dương của bất phương trình (2 - x)(x + 1)(3 - x) bé hơn bằng 0 là A. 1.B. 4.C. 2.D. 3. (ảnh 1)

Suy ra $x \in (- \infty; - 1] \cup [2; 3]$ .

Vậy số nghiệm nguyên dương của bất phương trình trên là 2.

Câu 5:

Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?

A. $2 x - 5 y + 3 z \leq 0$ .

B. $3 x^{2} + 2 x - 4 > 0$ .

C. $2 x^{2} + 5 y > 3$ .

D. $2 x + 3 y < 5$ .

Xem đáp án

Chọn đáp án D

Bất phương trình bậc nhất hai ẩn là bất phương trình có dạng ax + by + c > 0 (hoặc ax + by + c ≥ 0, ax + by + c < 0, ax + by + c ≤ 0).

Do đó chỉ có đáp án D là thỏa mãn

Câu 6:

Điều kiện xác định của bất phương trình

\frac{2 x}{|x + 1| - 3} - \frac{1}{\sqrt{2 - x}} \geq 1

là

A. $x \leq 2$ .

B. $\{\begin{cases} x \neq 2 \\ x \neq - 4 \end{cases}$ .

C. $\{\begin{cases} x < 2 \\ x \neq - 4 \end{cases}$ .

D. x < 2.

Xem đáp án

Chọn đáp án C

Điều kiện xác định của bất phương trình $\frac{2 x}{|x + 1| - 3} - \frac{1}{\sqrt{2 - x}} \geq 1$ là

$\{\begin{cases} |x + 1| - 3 \neq 0 \\ 2 - x > 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq 2 \\ x \neq - 4 \\ x < 2 \end{cases} \Leftrightarrow \{\begin{cases} x \neq - 4 \\ x < 2 \end{cases}$

Câu 7:

Cho các bất đẳng thức a > b và c > d. Bất đẳng thức nào sau đây đúng

A. a – c > b – d

B. a + c > b + d

C. ac > bd

D. $\frac{a}{c} > \frac{b}{d}$

Xem đáp án

Chọn đáp án B

Ta có: a > b và c > d

Suy ra a + c > b + d

Câu 8:

Tập nghiệm của hệ bất phương trình

\{\begin{cases} 4 - x \geq 0 \\ x + 2 \geq 0 \end{cases}

là

A. $S = (- \infty; - 2] \cup [4; + \infty)$ .

B. $S = [- 2; 4]$ .

C. $S = [2; 4]$ .

D. $S = (- \infty; - 2) \cup (4; + \infty)$ .

Xem đáp án

Chọn đáp án B

$\{\begin{cases} 4 - x \geq 0 \\ x + 2 \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \leq 4 \\ x \geq - 2 \end{cases} \Leftrightarrow - 2 \leq x \leq 4$ .

Vậy tập nghiệm của hệ bất phương trình là: [-2;4].

Câu 9:

Bảng xét dấu sau là của biểu thức nào?

A. $f (x) = x - 2$ .

B. $f (x) = 2 - 4 x$ .

C. $f (x) = 16 - 8 x$ .

D. $f (x) = - x - 2$ .

Xem đáp án

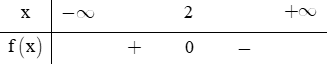
Chọn đáp án C

Ta thấy f(x) = 16 – 8x có nghiệm x = 2 đồng thời hệ số a = - 8 < 0 nên bảng xét dấu trên là của biểu thức f(x) = 16 – 8x .

Câu 10:

Cho tam giác ABC, có độ dài ba cạnh là BC = a, AC = b, AB = c. Gọi m_a là độ dài đường trung tuyến kẻ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác và S là diện tích tam giác đó. Mệnh đề nào sau đây sai?

A. $m_{a}^{2} = \frac{b^{2} + c^{2}}{2} - \frac{a^{2}}{4}$ .

B. $a^{2} = b^{2} + c^{2} + 2 b c \cos A$ .

C. $S = \frac{a b c}{4 R}$ .

D. $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R$ .

Xem đáp án

Chọn đáp án B

Theo định lý hàm số cosin trong tam giác ta có $a^{2} = b^{2} + c^{2} - 2 b c \cos A$ .

Câu 11:

Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 2x + y < 1?

A. (-2;1).

B. (3;-7).

C. (0;1).

D. (0;0).

Xem đáp án

Chọn đáp án C

Đáp án A. Thay x = -2 và y = 1 vào BPT đã cho, ta được 2.(-2) + 1 < 1 ⇔ - 3 < 1 (luôn đúng). Do đó (-2;1) là nghiệm của bất phương trình đã cho.

Đáp án B. Thay x = 3 và y = - 7 vào BPT đã cho, ta được 2.3 + -7 < 1 ⇔ - 1 < 1 (luôn đúng). Do đó (3;-7) là nghiệm của bất phương trình đã cho.

Đáp án C. Thay x = 0 và y = 1 vào BPT đã cho, ta được 2.0 + 1 < 1 ⇔ 1 < 1 (vô lí). Do đó (0;1) là nghiệm của bất phương trình đã cho.

Đáp án D. Thay x = 0 và y = 0 vào BPT đã cho, ta được 2.0 + 0 < 1 ⇔ 0 < 1 (luôn đúng). Do đó (0;0) là nghiệm của bất phương trình đã cho.

Vậy chỉ có cặp số (0;1) không thỏa bất phương trình.

Câu 12:

Tìm giá trị của tham số m để phương trình

x^{2} - (m - 2) x + m^{2} - 4 m = 0

có hai nghiệm trái dấu.

A. 0 < m < 4.

B. m < 0 hoặc m > 4.

C. m > 2.

D. m < 2.

Xem đáp án

Chọn đáp án A

Phương trình đã cho có hai nghiệm trái dấu khi $m^{2} - 4 m < 0 \Leftrightarrow 0 < m < 4$ .

Vậy tập xác định của hàm số là D = [-1;3].

Câu 13:

Tập nghiệm của bất phương trình

- x^{2} + x + 12 \geq 0

là

A. $(- \infty; - 3] \cup [4; + \infty)$ .

B. $\emptyset$ .

C. $(- \infty; - 4] \cup [3; + \infty)$ .

D. $[- 3; 4]$ .

Xem đáp án

Chọn đáp án D

Ta có $- x^{2} + x + 12 \geq 0 \Leftrightarrow - 3 \leq x \leq 4$ .

Vậy tập nghiệm của bất phương trình là $[- 3; 4]$ .

Câu 14:

Cho tam giác ABC thoả mãn:

b^{2} + c^{2} - a^{2} = \sqrt{3} b c

. Khi đó:

A. $\hat{A} = 30^{0} .$

B. $\hat{A} = 45^{0} .$

C. $\hat{A} = 60^{0} .$

D. $\hat{A} = 75^{0}$ .

Xem đáp án

Chọn đáp án A

Xét tam giác ABC, có:

$\cos A = \frac{b^{2} + c^{2} - a^{2}}{2 b c} = \frac{\sqrt{3} b c}{2 b c} = \frac{\sqrt{3}}{2}$

$\Rightarrow \hat{A} = 30^{0}$

Câu 15:

Gọi

S = m_{a}^{2} + m_{b}^{2} + m_{c}^{2}

là tổng bình phương độ dài ba trung tuyến của tam giác ABC. Trong các mệnh đề sau mệnh đề nào đúng?

A. $S = \frac{3}{4} (a^{2} + b^{2} + c^{2})$ .

B. $S = (a^{2} + b^{2} + c^{2})$ .

C. $S = \frac{3}{2} (a^{2} + b^{2} + c^{2})$ .

D. $S = 3 (a^{2} + b^{2} + c^{2})$ .

Xem đáp án

Chọn đáp án A

Ta có:

S = m_{a}^{2} + m_{b}^{2} + m_{c}^{2} = \frac{b^{2} + c^{2}}{2} - \frac{a^{2}}{4} + \frac{a^{2} + c^{2}}{2} - \frac{b^{2}}{4} + \frac{a^{2} + b^{2}}{2} - \frac{c^{2}}{4} = \frac{3}{4} (a^{2} + b^{2} + c^{2}) .

Câu 16:

Trong hệ trục tọa độ Oxy, Véctơ nào là một véctơ pháp tuyến của đường thẳng

d : \{\begin{cases} x = - 2 - t \\ y = - 1 + 2 t \end{cases}

?

A. $\vec{n} (- 2; - 1)$ .

B. $\vec{n} (2; - 1)$ .

C. $\vec{n} (- 1; 2)$ .

D. $\vec{n} (1; 2)$ .

Xem đáp án

Chọn đáp án A

Đường thẳng $d : \{\begin{cases} x = - 2 - t \\ y = - 1 + 2 t \end{cases}$ có VTCP là” (-1;2)

Do đó VTPT của đường thẳng d là: $\vec{n} (- 2; - 1)$ .

Câu 17:

Cho đường thẳng

Δ : x - 2 y + 3 = 0

. Véc tơ nào sau đây không là véc tơ chỉ phương của

Δ

?

A. $\vec{u} = (4; - 2)$ .

B. $\vec{v} = (- 2; - 1)$ .

C. $\vec{m} = (2; 1)$ .

D. $\vec{q} = (4; 2)$ .

Xem đáp án

Chọn đáp án A

Đường thẳng $Δ : x - 2 y + 3 = 0$ có VTPT của $Δ$ là $\vec{n} = (1; - 2)$

Khi đó VTCP của đường thẳng Δ là (2;1).

Do đó véc tơ $\vec{u} = (4; - 2)$ không phải là véc tơ chỉ phương của $Δ$ .

Câu 18:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng cắt hai trục Ox, Oy lần lượt tại hai điểm A(a; 0), B(0; b),

(a, b \neq 0)

. Viết phương trình đường thẳng d.

A. $d : \frac{x}{a} - \frac{y}{b} = 1$ .

B. $d : \frac{x}{b} + \frac{y}{a} = 1$ .

C. $d : \frac{x}{a} + \frac{y}{b} = 1$ .

D. $d : \frac{x}{a} + \frac{y}{b} = 0$ .

Xem đáp án

Chọn đáp án C

Vì d cắt hai trục Ox, Oy lần lượt tại hai điểm A(a; 0), B(0; b) nên phương trình đoạn chắn d là: $d : \frac{x}{a} + \frac{y}{b} = 1$

Câu 19:

Viết phương trình chính tắc của đường thẳng

∆

đi qua M(1; -3) và nhận vectơ

\vec{u} (1; 2)

làm vectơ chỉ phương.

A. $Δ : 2 x - y - 5 = 0.$

B. $Δ : \frac{x - 1}{1} = \frac{y + 3}{2} \cdot$

C. $Δ : \{\begin{cases} x = 1 + t \\ y = - 3 + 2 t \end{cases} \cdot$

D. $Δ : \frac{x + 1}{1} = \frac{y - 3}{2} \cdot$

Xem đáp án

Chọn đáp án B

Đường thẳng D đi qua M(1; -3) và nhận vectơ

\vec{u} (1; 2)

làm vectơ chỉ phương có phương trình chính tắc là

\frac{x - 1}{1} = \frac{y + 3}{2}

Câu 20:

Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A. B, C, D?

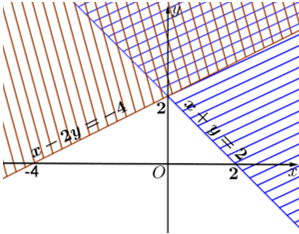
Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong (ảnh 1)

A. $\{\begin{cases} x + y \leq 2 \\ x - 2 y \geq - 4 \end{cases} .$

B. $\{\begin{cases} x + y \geq 2 \\ x - 2 y \geq - 4 \end{cases} .$

C. $\{\begin{cases} x + y \geq 2 \\ x - 2 y \leq - 4 \end{cases} .$

D. $\{\begin{cases} x + y \leq 2 \\ x - 2 y \leq - 4 \end{cases} .$

Xem đáp án

Chọn đáp án A

Xét hệ phương trình ở đáp án A $\{\begin{cases} x + y \leq 2 \\ x - 2 y \geq - 4 \end{cases}$

Thay điểm O(0;0) vào bất phương trình thứ nhất $0 + 0 \leq 2$ thỏa mãn nên gạch bỏ phần ko chứa điểm O.

Thay điểm O(0;0) vào bất phương trình thứ nhất $0 - 2.0 \geq - 4$ thỏa mãn nên gạch bỏ phần ko chứa điểm O.

Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương

\{\begin{cases} x + y \leq 2 \\ x - 2 y \geq - 4 \end{cases}

Câu 21:

Cho

x^{2} + y^{2} = 1

, gọi S = x + y. Khi đó ta có

A. $S \leq \sqrt{2}$

B. $S \geq \sqrt{2}$

C. $- \sqrt{2} \leq S \leq \sqrt{2}$

D. $- 1 \leq S \leq 1$

Xem đáp án

Chọn đáp án C

Ta có: $1 = x^{2} + y^{2} \geq 2 x y \Rightarrow 2 x y \leq 1$

Mặt khác:

S^{2} = {(x + y)}^{2} = x^{2} + 2 x y + y^{2} \leq 2 \Rightarrow - \sqrt{2} \leq S \leq \sqrt{2}

Câu 22:

Tập nghiệm của bất phương trình

\frac{3 x - 4}{x - 2} \leq 1

là:

A. $S = (1; 2]$

B. $S = [1; 2]$

C. $S = [1; 2)$

D. $S = (- \infty; 1] \cup (2; + \infty)$

Xem đáp án

Chọn đáp án C

$\frac{3 x - 4}{x - 2} \leq 1 \Leftrightarrow \frac{3 x - 4}{x - 2} - 1 \leq 0 \Leftrightarrow \frac{3 x - 4 - x + 2}{x - 2} \leq 0 \Leftrightarrow \frac{2 x - 2}{x - 2} \leq 0$

Nên tập nghệm của bất phương trình là [1;2).

Câu 23:

Tập nghiệm của bất phương trình

|2 x - 4| \leq x + 12

là

A. $S = [- \frac{8}{3}; + \infty)$

B. $S = (- \frac{8}{3}; 16)$

C. $S = (- \infty; 16]$

D. $S = [- \frac{8}{3}; 16]$

Xem đáp án

Chọn đáp án D

TH1: $x \geq 2$ bpt tương đương với $2 x - 4 \leq x + 12 \Leftrightarrow x \leq 16$ nên $2 \leq x \leq 16$

TH2: x < 2 bpt tương đương với $- 2 x + 4 \leq x + 12 \Leftrightarrow - 3 x \leq 8 \Leftrightarrow x \geq - \frac{8}{3}$ nên $- \frac{8}{3} \leq x < 2$

Kết hợp cả 2 trường hợp ta được tập nghiệm $- \frac{8}{3} \leq x \leq 16.$

Câu 24:

Cho bất phương trình

|\frac{2}{x - 13}| > \frac{8}{9}

. Số nghiệm nguyên nhỏ hơn 13 của bất phương trình là

A. 3.

B. 1.

C. 2.

D. 0.

Xem đáp án

Chọn đáp án C

Với $x < 13 \Leftrightarrow x - 13 < 0$ thì

$|\frac{2}{x - 13}| > \frac{8}{9} \Leftrightarrow - \frac{2}{x - 13} - \frac{8}{9} > 0 \Leftrightarrow \frac{- 18 - 8 (x - 13)}{9 (x - 13)} > 0$

$\Leftrightarrow \frac{- 8 x + 86}{9 (x - 13)} > 0 \Leftrightarrow - 8 x + 86 < 0 \Leftrightarrow x > \frac{43}{4}$

Vì $x \in ℤ, \frac{43}{4} < x < 13$ nên $x \in \{11; 12\}$

Câu 25:

Bất phương trình:

|3 x - 2| (x^{2} + 1) \geq 0

có tập nghiệm là:

A. $(\frac{2}{3}; + \infty)$ .

B. $[\frac{2}{3}; + \infty)$ .

C. $(- \infty; \frac{2}{3})$ .

D. $ℝ$ .

Xem đáp án

Chọn đáp án D

Ta có:

\begin{array}{l} |3 x - 2| \geq 0, \forall x \\ (x^{2} + 1) > 0, \forall x \end{array}\} \Rightarrow |3 x - 2| (x^{2} + 1) \geq 0, \forall x \in ℝ

Câu 26:

Cho tam giác ABC, các đường cao

h_{a}, h_{b}, h_{c}

thỏa mãn hệ thức

3 h_{a} = 2 h_{b} + h_{c}

. Tìm hệ thức giữa a, b, c.

A. $\frac{3}{a} = \frac{2}{b} - \frac{1}{c}$ .

B. 3a = 2b + c.

C. 3a = 2b – c.

D. $\frac{3}{a} = \frac{2}{b} + \frac{1}{c}$ .

Xem đáp án

Chọn đáp án D

Kí hiệu $S = S_{△ A B C}$ .

Ta có:

3 h_{a} = 2 h_{b} + h_{c} \Leftrightarrow \frac{3.2 S}{a} = \frac{2.2 S}{b} + \frac{2 S}{c} \Leftrightarrow \frac{3}{a} = \frac{2}{b} + \frac{1}{c}

Câu 27:

Tam giác ABC có

A = 120 °

thì câu nào sau đây đúng?

A. a² = b² + c² – 3bc.

B. a² = b² + c² + bc.

C. a² = b² + c² + 3bc.

D. a² = b² + c² – bc.

Xem đáp án

Chọn đáp án B

Áp dụng định lí hàm số cos tại đỉnh A ta có: $a^{2} = b^{2} + c^{2} - 2 b c . \cos A$ .

$\Rightarrow a^{2} = b^{2} + c^{2} - 2 b c . c os 120 ° \Rightarrow a^{2} = b^{2} + c^{2} + b c$ .

Câu 28:

Tập xác định của hàm số

y = \sqrt{x + 2} + \frac{1}{\sqrt{x^{2} - x - 6}}

là:

A. $D = (- 2; + \infty) .$

B. $D = (- 2; 3) .$

C. $D = (3; + \infty) .$

D. $D = (- \infty; - 2] .$

Xem đáp án

Chọn đáp án C

Điều kiện $\{\begin{cases} x + 2 \geq 0 \\ x^{2} - x - 6 > 0 \end{cases} \Leftrightarrow \{\begin{matrix} x \geq - 2 \\ [\begin{matrix} x < - 2 \\ x > 3 \end{matrix} \end{matrix} \Leftrightarrow x > 3.$

Vậy tập xác định $D = (3; + \infty) .$

Câu 29:

Nghiệm của bất phương trình

\frac{x^{2} + x - 1}{x^{2} + 4} < \frac{x^{2} + x}{x^{2} + 4}

là:

A. x > 1.

B. x < 1.

C. x > 4.

D. $x \in ℝ .$

Xem đáp án

Chọn đáp án D

Ta có $x^{2} + 4 > 0 \forall x \in ℝ$

Bất phương trình tương đương với $x^{2} + x - 1 < x^{2} + x \Leftrightarrow - 1 < 0$ đúng với $\forall x \in ℝ$ .

Câu 30:

Giải bất phương trình

|x + 1| + |x - 4| > 7

. Giá trị nghiệm nguyên dương nhỏ nhất của x thoả bất phương trình là

A. x = 9.

B. x = 8.

C. x = 7.

D. x = 6.

Xem đáp án

Chọn đáp án D

Xét dấu phá trị tuyệt đối:

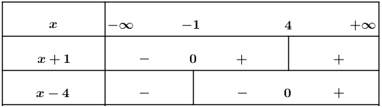
Giải bất phương trình |x + 1| + |x - 4| > 7. Giá trị nghiệm nguyên dương nhỏ nhất của x thoả bất (ảnh 1)

TH1. $x \in (- \infty; - 1)$

$|x + 1| + |x - 4| > 7 \Leftrightarrow \{\begin{cases} x \in (- \infty; - 1) \\ - (x + 1) - (x - 4) > 7 \end{cases}$

$\Leftrightarrow \{\begin{cases} x \in (- \infty; - 1) \\ - 2 x + 3 > 7 \end{cases} \Leftrightarrow \{\begin{cases} x \in (- \infty; - 1) \\ x < - 2 \end{cases} \Leftrightarrow x \in (- \infty; - 2)$

TH2. $x \in [- 1; 4)$

$|x + 1| + |x - 4| > 7 \Leftrightarrow \{\begin{cases} x \in [- 1; 4) \\ (x + 1) - (x - 4) > 7 \end{cases} \Leftrightarrow \{\begin{cases} x \in [- 1; 4) \\ 5 > 7 \end{cases} \Leftrightarrow x \in \emptyset$

TH3. $x \in [4; + \infty)$

$|x + 1| + |x - 4| > 7 \Leftrightarrow \{\begin{cases} x \in [4; + \infty) \\ (x + 1) + (x - 4) > 7 \end{cases} \Leftrightarrow \{\begin{cases} x \in [4; + \infty) \\ 2 x - 3 > 7 \end{cases}$

$\Leftrightarrow \{\begin{cases} x \in [4; + \infty) \\ x > 5 \end{cases} \Leftrightarrow x \in (5; + \infty)$

Tổng hợp lại, tập nghiệm của bất phương trình là:

T = (- \infty; - 2) \cup (5; + \infty) .

Câu 31:

Phương trình của đường thẳng qua

A (1; 4)

và cách

B (- 3; 1)

một khoảng bằng 3 là:

A. 24x + 7y – 52 = 0.

B. x = 4, y = 4.

C. y = 4, 24x – 7y + 4 = 0.

D. x = 4, 24x + 7y – 52 = 0.

Xem đáp án

Chọn đáp án C

$Δ$ qua $A (1; 4) \Rightarrow Δ : a (x - 1) + b (y - 4) = 0 \Leftrightarrow a x + b y - a - 4 b = 0$

$d (B, Δ) = 3 \Leftrightarrow \frac{|- 3 a + b - a - 4 b|}{\sqrt{a^{2} + b^{2}}} = 3 \Leftrightarrow |- 4 a - 3 b| = 3 \sqrt{a^{2} + b^{2}}$

$\Leftrightarrow 7 a^{2} + 24 a b = 0 \Leftrightarrow [\begin{array}{l} a = 0 \\ a = - \frac{24}{7} b \end{array}$

Với a = 0, chọn $b = 1 \Rightarrow Δ : y = 4$

Với $a = - \frac{24}{7} b$ , chọn $b = - 7 \Rightarrow a = 24 \overset{}{\to} Δ : 24 x - 7 y + 4 = 0$

Câu 32:

Với giá trị nào của m thì 2 đường thẳng sau đây vuông góc?

$Δ_{1} : (2 m - 1) x + m y - 10 = 0$ và $Δ_{2} : 3 x + 2 y + 6 = 0$

A. m = 0.

B. $m \in \emptyset$ .

C. m = 2.

D. $m = \frac{3}{8} \cdot$

Xem đáp án

Chọn đáp án D

$Δ_{1}$ có vectơ pháp tuyến là ${\vec{n}}_{1} = (2 m - 1; m)$ , $Δ_{2}$ có vectơ pháp tuyến là $\vec{n_{2}} = (3; 2)$ .

Ta có:

Δ_{1} ⊥ Δ_{2} \Leftrightarrow \vec{n_{1}} . \vec{n_{2}} = 0 \Leftrightarrow 3 (2 m - 1) + 2 m = 0 \Leftrightarrow m = \frac{3}{8} \cdot

Câu 33:

Giá trị nhỏ nhất của hàm số

f (x) = \frac{x}{2} + \frac{2}{x - 1}

với x > 1 là

A. 2.

B. $\frac{5}{2}$ .

C. $2 \sqrt{2}$ .

D. 3.

Xem đáp án

Chọn đáp án B

Ta có $f (x) = \frac{x}{2} + \frac{2}{x - 1} = \frac{x - 1}{2} + \frac{2}{x - 1} + \frac{1}{2} \geq 2 \sqrt{\frac{x - 1}{2} . \frac{2}{x - 1}} + \frac{1}{2} = \frac{5}{2}$

Dấu "=" xảy ra khi và chỉ khi $\frac{x - 1}{2} = \frac{2}{x - 1} \Leftrightarrow x = 3, (x > 1)$

Vậy giá trị nhỏ nhất của hàm số là $\frac{5}{2}$ khi x = 3.

Câu 34:

Đường thẳng

Δ : 5 x + 3 y = 15

tạo với các trục tọa độ một tam giác có diện tích bằng bao nhiêu?

A. 3.

B. 15.

C. 7,5.

D. 5.

Xem đáp án

Chọn đáp án C

Gọi A là giao điểm của $Δ$ và Ox, B là giao điểm của $Δ$ và Oy.

Ta có: $A (3; 0), B (0; 5) \Rightarrow O A = 3, O B = 5 \Rightarrow S_{Δ O A B} = \frac{15}{2}$

Câu 35:

Viết phương trình tổng quát của đường thẳng

Δ

đi qua điểm M(1;1) và song song với đường thẳng có phương trình

d : (\sqrt{2} - 1) x + y + 1 = 0

.

A. $(\sqrt{2} - 1) x + y = 0$ .

B. $x + (\sqrt{2} + 1) y - 2 \sqrt{2} = 0$ .

C. $(\sqrt{2} - 1) x - y + 2 \sqrt{2} - 1 = 0$ .

D. $(\sqrt{2} - 1) x + y - \sqrt{2} = 0$ .

Xem đáp án

Chọn đáp án D

Vì $Δ // d \Rightarrow Δ : (\sqrt{2} - 1) x + y + c = 0 (c \neq 1)$

Và $M (1; 1) \in Δ$ nên $Δ : (\sqrt{2} - 1) x + y - \sqrt{2} = 0$ .

Câu 36:

Giải bất phương trình

\sqrt{x^{2} + x - 12} < 6 - x

.

Xem đáp án

$\sqrt{x^{2} + x - 12} < 6 - x \Leftrightarrow \{\begin{cases} 6 - x > 0 \\ x^{2} + x - 12 \geq 0 \\ x^{2} + x - 12 < {(6 - x)}^{2} \end{cases}$

$\Leftrightarrow \{\begin{cases} x < 6 \\ x \in (- \infty; - 4] \cup [3; + \infty) \\ x^{2} + x - 12 < 36 - 12 x + x^{2} \end{cases}$

$\Leftrightarrow \{\begin{cases} x < 6 \\ x \in (- \infty; - 4] \cup [3; + \infty) \\ 13 x < 48 \end{cases}$

$\Leftrightarrow \{\begin{cases} x < 6 \\ x \in (- \infty; - 4] \cup [3; + \infty) \\ x < \frac{48}{13} \end{cases}$

$\Leftrightarrow x \in (- \infty; - 4] \cup [3; \frac{48}{13})$

Vậy tập nghiệm của bất phương trình là

S = (- \infty; - 4] \cup [3; \frac{48}{13})

Câu 37:

Cho tam giác ABC có $\hat{A} = 60 °; A B = 6, A C = 9$ . Tính diện tích S và đường cao AH của tam giác ABC.

Xem đáp án

$S = \frac{1}{2} . A B . A C . \sin A = \frac{1}{2} .6.9. \sin 60 ° = \frac{27 \sqrt{3}}{2}$

$B C^{2} = A B^{2} + A C^{2} - 2 A B . A C . c o s 60 °$

$= 6^{2} + 9^{2} - 2.6.9. \cos 60 ° = 63 \Rightarrow B C = 3 \sqrt{7}$

$S = \frac{1}{2} B C . A H \Rightarrow A H = \frac{2. S}{B C} = \frac{27 \sqrt{3}}{3 \sqrt{7}} = \frac{9 \sqrt{21}}{7}$

Câu 38:

Trong mặt phẳng với hệ tọa độ Oxy cho đường thằng $d : 3 x - 4 y + 1 = 0$ . Tìm tọa độ điểm M trên trục Ox sao cho điểm M cách đường thẳng d một khoảng bằng 2.

Xem đáp án

Điểm $M \in O x$ nên có tọa độ dạng M(m; 0).

Khi đó $d (M, O x) = \frac{|3. m - 4.0 + 1|}{\sqrt{3^{2} + {(- 4)}^{2}}} = \frac{|3 m + 1|}{5}$

Theo giả thiết ta có phương trình $\frac{|3 m + 1|}{5} = 2 \Leftrightarrow [\begin{array}{l} 3 m + 1 = 10 \\ 3 m + 1 = - 10 \end{array} \Leftrightarrow [\begin{array}{l} m = 3 \\ m = - \frac{11}{3} \end{array}$

Vậy có hai điểm thỏa mãn là

M_{1} (3; 0); M_{2} (- \frac{11}{3}; 0)

.

Câu 39:

Cho a, b là các số dương thỏa mãn

a^{2} + b^{2} = 2

. Chứng minh rằng

(\frac{a}{b} + \frac{b}{a}) (\frac{a}{b^{2}} + \frac{b}{a^{2}}) \geq 4

.

Xem đáp án

Áp dụng BĐT côsi ta có

$\frac{a}{b} + \frac{b}{a} \geq 2 \sqrt{\frac{a}{b} . \frac{b}{a}} = 2, \frac{a}{b^{2}} + \frac{b}{a^{2}} \geq 2 \sqrt{\frac{a}{b^{2}} . \frac{b}{a^{2}}} = \frac{2}{\sqrt{a b}}$

Suy ra $(\frac{a}{b} + \frac{b}{a}) (\frac{a}{b^{2}} + \frac{b}{a^{2}}) \geq \frac{4}{\sqrt{a b}}$ (1)

Mặt khác ta có $2 = a^{2} + b^{2} \geq 2 \sqrt{a^{2} b^{2}} = 2 a b \Rightarrow a b \leq 1$ (2)

Từ (1) và (2) suy ra $(\frac{a}{b} + \frac{b}{a}) (\frac{a}{b^{2}} + \frac{b}{a^{2}}) \geq 4$ (ĐPCM).

Đẳng thức xảy ra khi và chỉ khi a = b = 1.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra giữa học kì 2 Toán 10 có đáp án (Mới nhất)

Đề kiểm tra giữa học kì 2 Toán 10 có đáp án (Mới nhất) (Đề 10)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương