Đề kiểm tra giữa học kì 2 Toán 10 có đáp án (Mới nhất) (Đề 4)
-
1480 lượt thi
-
50 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
![Tập xác định của hàm số y = căn bậc 2( x^2 + 1/1-x) là A. D = (1; + vô cùng) B. D = R \{1} C. D = (- vô cùng; 1) D. D = (- vô cùng; 1] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/07/anh3-1656755084.png) là
làChọn đáp án C
Hàm số đã cho xác định khi và chỉ khi ![Tập xác định của hàm số y = căn bậc 2( x^2 + 1/1-x) là A. D = (1; + vô cùng) B. D = R \{1} C. D = (- vô cùng; 1) D. D = (- vô cùng; 1] (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/07/anh1-1656755008.png)
Câu 2:
Chọn đáp án A
Phương trình xác định khi 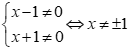 .
.
Phương trình![]()
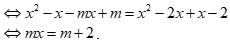
Để phương trình có nghiệm duy nhất thì 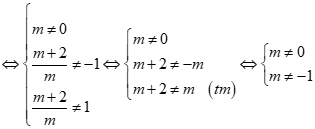
Câu 3:
Chọn đáp án A
Phương trình có hai nghiệm x1, x2 khi
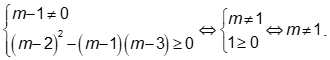
Khi đó 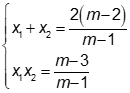
Theo đề, ta có ![]()
![]()
So với điều kiện, ta có ![]()
Câu 4:
Chọn đáp án C
Điều kiện xác định ![]() .
.
Với điều kiện đó, phương trình đã cho tương đương
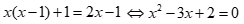
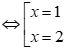
Đối chiếu điều kiện ta có x=2 là nghiệm duy nhất của phương trình.
Vậy phương trình đã cho có 1 nghiệm.
Câu 5:
Chọn đáp án C
PT 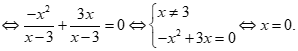
Vậy tập nghiệm phương trình là S = {0}.
Câu 6:
Chọn đáp án C
![]() (1)
(1)
Vì 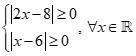 nên phương trình (1)
nên phương trình (1) ![]()
Vậy phương trình (1) vô nghiệm.
Câu 7:
Chọn đáp án D
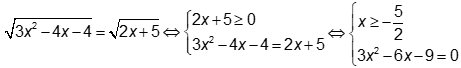
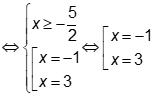
Câu 8:
Chọn đáp án D.
Xét phương trình: ![]()
Điều kiện: 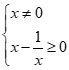
Chia hai vế phương trình cho ![]() ta được:
ta được:
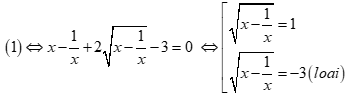
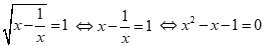 . Vì ac = -1 < 0 nên phương trình này có hai nghiệm phân biệt thỏa mãn điều kiện và có tích là x1.x2 = -1
. Vì ac = -1 < 0 nên phương trình này có hai nghiệm phân biệt thỏa mãn điều kiện và có tích là x1.x2 = -1 Câu 9:
Chọn đáp án D
Ta có ![]() , suy ra khẳng định D sai.
, suy ra khẳng định D sai.
Câu 11:
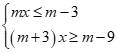 có nghiệm duy nhất khi và chỉ khi
có nghiệm duy nhất khi và chỉ khiChọn đáp án A
Hệ có nghiệm duy nhất khi và chỉ khi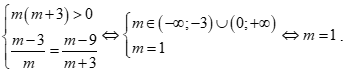
Câu 12:
Chọn đáp án C
Cách 1: Thay x = -2 lần lượt vào phương án A, B, C, D thì phương án C là đúng.
Cách 2:
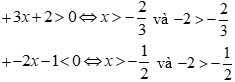
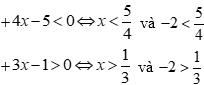
Câu 13:
Chọn đáp án D
Nhị thức bậc nhấtCâu 16:
Chọn đáp án B
+ Với ![]() thì ax + b > 0 có tập nghiệm
thì ax + b > 0 có tập nghiệm ![]() , đáp án A sai.
, đáp án A sai.
+ Với ![]() thì b > 0 có tập nghiệm
thì b > 0 có tập nghiệm ![]() , đáp án B đúng.
, đáp án B đúng.
+ Với ![]() thì ax > 0 có tập nghiệm
thì ax > 0 có tập nghiệm ![]() , đáp án C sai.
, đáp án C sai.
+ Với ![]() thì b > 0 vô nghiệm, đáp án D sai.
thì b > 0 vô nghiệm, đáp án D sai.
Câu 17:
Chọn đáp án B
Ta có dấu của bất phương trình ![]() cũng là dấu của bất phương trình
cũng là dấu của bất phương trình ![]()
![]()
Vậy tập nghiệm của bất phương trình đã cho là ![]()
Câu 18:
Chọn đáp án B
Theo định lí về dấu của tam thức bậc hai.
Câu 21:
Cho các mệnh đề
(I) với mọi ![]() thì
thì ![]() .
.
(II) với mọi ![]() thì
thì ![]() .
.
(III) với mọi ![]() thì
thì ![]() .
.
Chọn đáp án A
Ta có ![]() . Vậy (I) đúng.
. Vậy (I) đúng.
![]() Vậy (II) sai.
Vậy (II) sai.
![]() Vậy (III) đúng.
Vậy (III) đúng.
Câu 22:
Chọn đáp án D
- Xét đáp án A: ![]()
Ta thấy 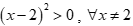 và
và ![]() với mọi x < 10.
với mọi x < 10.
Tập nghiệm của bất phương trình là ![]() .
.
- Xét đáp án B: 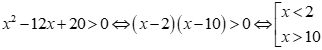
Tập nghiệm của bất phương trình là ![]() .
.
- Xét đáp án C: 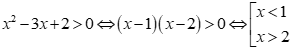
Tập nghiệm của bất phương trình là ![]() .
.
Xét đáp án D: ![]() .
.
Câu 23:
Chọn đáp án D
![]()
Suy ra ![]() . Do đó
. Do đó ![]()
Câu 25:
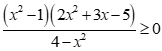 là
làChọn đáp án B
Ta có:
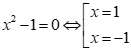
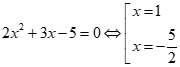
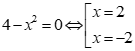
Trục xét dấu:
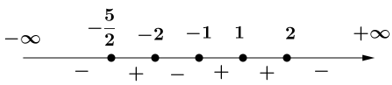
Tập nghiệm của bất phương trình là ![]()
Câu 27:
Chọn đáp án A
Đặt ![]() .
.
Khi đó bất phương trình trở thành ![]()
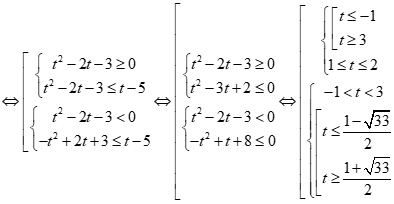 Vô nghiệm.
Vô nghiệm.
Vậy bất phương trình đã cho vô nghiệm.
Câu 28:
Chọn đáp án B
![]()
+) 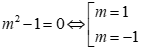
Với m = 1bất phương trình có dạng ![]() . Do đó m = 1 không thoả mãn.
. Do đó m = 1 không thoả mãn.
Với m = -1 bất phương trình có dạng ![]() . Do đó m = -1 là một giá trị cần tìm.
. Do đó m = -1 là một giá trị cần tìm.
+) ![]() . Khi đó vế trái là tam thức bậc hai có
. Khi đó vế trái là tam thức bậc hai có ![]() nên
nên
tam thức luôn có 2 nghiệm x1 < x2.
Suy ra mọi ![]() đều là nghiệm của bất phương trình
đều là nghiệm của bất phương trình ![]() khi và chỉ khi
khi và chỉ khi 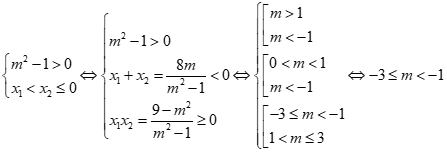 .
.
Câu 29:
Chọn đáp án A
Nhận thấy ![]() với mọi m nên f(x) là một tam thức bậc 2.
với mọi m nên f(x) là một tam thức bậc 2.
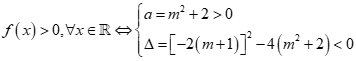
Câu 30:
Chọn đáp án B
Ta có: ![]()
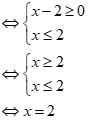
Vậy tập nghiệm của bất phương trình là ![]()
Câu 31:
Chọn đáp án C
Điều kiện: ![]()
![]() không thỏa điều kiện.
không thỏa điều kiện.
Vậy ![]() .
.
Câu 32:
Chọn đáp án C
![]()
Điều kiện: ![Tính tổng các nghiệm nguyên thuộc [-5; 5] của bất phương trình căn bậc 2(x^2 -9)(3x - 1/x + 5) bé hơn bằng (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2022/07/anh2-1656837405.png)
- Nếu ![]() , bất phương trình đúng.
, bất phương trình đúng.
- Nếu![Tính tổng các nghiệm nguyên thuộc [-5; 5] của bất phương trình căn bậc 2(x^2 -9)(3x - 1/x + 5) bé hơn bằng (ảnh 5)](https://video.vietjack.com/upload2/quiz_source1/2022/07/blobid0-1656837436.png)
Mà ![]()
Nên ![]()
Câu 33:
Chọn đáp án C
Bất phương trình: ![]()
Điều kiện: ![]()
Bất phương trình tương đương: 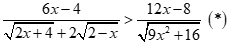
+ Với ![]() không thỏa mãn.
không thỏa mãn.
+ Với ![]() , ta có:
, ta có:
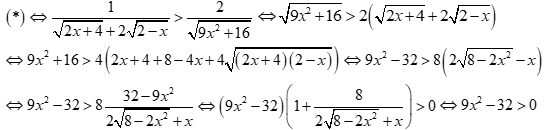
![]() hoặc
hoặc ![]()
Suy ra 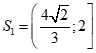
+ Với ![]() , ta có: (*)
, ta có: (*) ![]() ,
,
![]() đúng với
đúng với ![]()
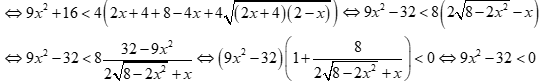
Suy ra ![]()
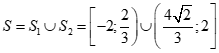
Câu 34:
Chọn đáp án B
Áp dụng định lý cosin cho tam giác , ta có:
![]()
![]()
![]()
Câu 35:
Chọn đáp án B
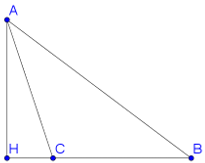
Do ![]() .
.
![]() như hình vẽ.
như hình vẽ.
Áp dụng hệ quả ĐL cosin cho tam giác ABC ta có:
![]()
Khi đó: ![]()
Mà ![]()
Câu 36:
Chọn đáp án D
Trong tam giác ABC với BC = a, AC = b, AB = c
Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau khi và chỉ khi 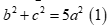
Mặt khác theo định lí cô sin trong tam giác, ta có 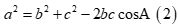
Từ (1) và (2) suy ra 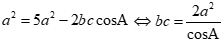
Diện tích tam giác 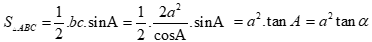
Chứng minh bài toán: Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau khi và chỉ khi 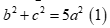
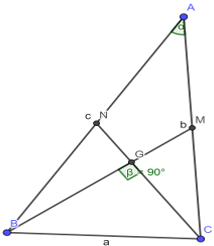
Ta có: 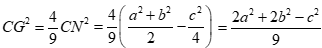
Tương tự, ta có ![]()
Do 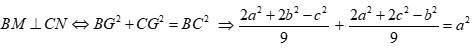
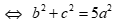
Câu 37:
Chọn đáp án A
Theo định lý sin ta có: ![]() .
.
Từ công thức ![]() nên phương án A sai.
nên phương án A sai.
Từ công thức ![]() nên phương án B đúng.
nên phương án B đúng.
Từ công thức ![]() nên phương án C đúng.
nên phương án C đúng.
Từ công thức ![]() nên phương án D đúng.
nên phương án D đúng.
Câu 38:
Chọn đáp án A
Trong tam giác ABC ta có,Câu 39:
Chọn đáp án D
Áp dụng công thức tính diện tíchCâu 40:
Chọn đáp án C
Đặt 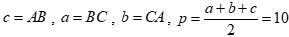
Diện tích tam giác ABC bằng 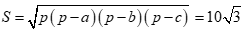
Bán kính đường tròn nội tiếp 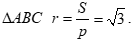
Câu 41:
Với các số đo trên hình vẽ sau, chiều cao h của tháp nghiêng Pisa gần với giá trị nào nhất?
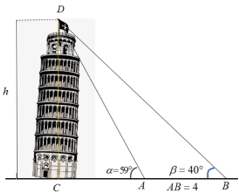
Chọn đáp án D
Xét tam giác ABD ta có: ![]()
Lại có: ![]()
Câu 42:
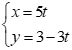 . Trong các điểm sau đây điểm nào không thuộc
. Trong các điểm sau đây điểm nào không thuộc Chọn đáp án B
Với ![]() thay x = -5, y = 6 vào phương trình
thay x = -5, y = 6 vào phương trình 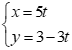 ta có:
ta có:
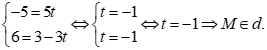
Với ![]() thay x = 5, y = 3 vào phương trình
thay x = 5, y = 3 vào phương trình 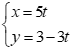 ta có:
ta có:
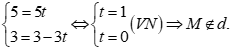
Với ![]() thay x = 0, y = 3 vào phương trình
thay x = 0, y = 3 vào phương trình 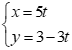 ta có:
ta có:
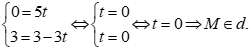
Với ![]() thay x = 5, y = 0 vào phương trình
thay x = 5, y = 0 vào phương trình 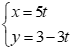 ta có:
ta có:
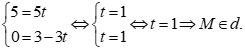
Câu 43:
Chọn đáp án C
Đường thẳngCâu 44:
Chọn đáp án D
Ta có, vectơ pháp tuyến của ![]() có dạng
có dạng ![]() với
với ![]() .
.
Đối chiếu các đáp án suy ra D sai.
Câu 45:
Chọn đáp án D
Đường thẳng AB đi qua hai điểm ![]() và
và ![]() nên đường thẳng AB nhận
nên đường thẳng AB nhận ![]() làm véc tơ chỉ phương hay nhận
làm véc tơ chỉ phương hay nhận ![]() làm véc tơ chỉ phương.
làm véc tơ chỉ phương.
Vậy đường thẳng AB đi qua ![]() và nhận
và nhận ![]() làm véc tơ chỉ phương có phương trình tham số là
làm véc tơ chỉ phương có phương trình tham số là ![]()
Câu 46:
Chọn đáp án A
Gọi d là đường thẳng đi qua ![]() và song song với đường thẳng
và song song với đường thẳng ![]() .
.
Đường thẳng ![]() có VTCP
có VTCP ![]() , thì đường thẳng d có VTCP
, thì đường thẳng d có VTCP ![]() .
.
Suy ra đường thẳng d có VTPT ![]() .
.
Phương trình tổng quát của đường thẳng d đi qua ![]() , VTPT
, VTPT ![]() có dạng:
có dạng:
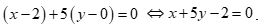
Câu 47:
Chọn đáp án B
Gọi M là trung điểm của cạnh BC ![]() .
.
![]()
Đường thẳng AM đi qua điểm ![]() nhận
nhận ![]() làm một vectơ pháp tuyến có phương trình là:
làm một vectơ pháp tuyến có phương trình là: ![]()
Câu 48:
Chọn đáp án A
Ta có ![]() nên tọa độ của A là nghiệm của hệ
nên tọa độ của A là nghiệm của hệ ![]() .
.
Ta có đường thẳng ![]() nên phương trình đường thẳng
nên phương trình đường thẳng ![]() .
.
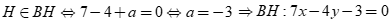
Ta có ![]() nên tọa độ của A là nghiệm của hệ
nên tọa độ của A là nghiệm của hệ 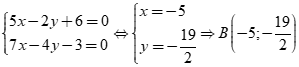 .
.
Câu 49:
Chọn đáp án D
Do ![]() nên tọa độ điểm M là nghiệm của hệ phương trình:
nên tọa độ điểm M là nghiệm của hệ phương trình:
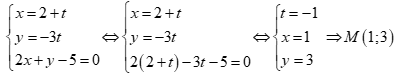
Câu 50:
Chọn đáp án C
![]()
Do tam giác ABC cân ở C nên
![]()
![]()
Suy ra ![]()

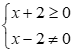
![Tập nghiệm của bất phương trình |5x - 4| lớn hơn bằng 6 có dạng S =( - Vô cùng; a] hợp [b; + Vô cùng). (ảnh 4)](https://video.vietjack.com/upload2/quiz_source1/2022/07/anh56-1656769213.png)

![Với x thuộc tập nào dưới đây thì f(x) = x(5x + 2) - x(x^2 + 6) không dương A. (1; 4). B. [1; 4]. C. [0; 1] hợp [4; + Vô cùng). (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/07/blobid1-1656772533.png)
![Với x thuộc tập nào dưới đây thì f(x) = x(5x + 2) - x(x^2 + 6) không dương A. (1; 4). B. [1; 4]. C. [0; 1] hợp [4; + Vô cùng). (ảnh 3)](https://video.vietjack.com/upload2/quiz_source1/2022/07/blobid2-1656772554.png)
![Tập nghiệm của hệ x^2 - 7x + 6 bé hơn bằng 0 x^2 - 8x + 15 bé hơn bằng 0 A. S = [5; 6].B. S = [1; 6].C. S = [1; 3].D. S = [3; 5]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/07/anh140-1656773218.png)
![Tập nghiệm của hệ x^2 - 7x + 6 bé hơn bằng 0 x^2 - 8x + 15 bé hơn bằng 0 A. S = [5; 6].B. S = [1; 6].C. S = [1; 3].D. S = [3; 5]. (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2022/07/blobid4-1656773091.png)