Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất) - Đề số 6
-
1404 lượt thi
-
5 câu hỏi
-
120 phút
Danh sách câu hỏi
Câu 1:
a) Cho biểu thức \(A = \sqrt {16} - \sqrt {25} + \sqrt 4 .\) So sánh A với \(\sqrt 2 \)
b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x - y = - 5\\2x + y = 11\end{array} \right.\)
a) Cho biểu thức \(A = \sqrt {16} - \sqrt {25} + \sqrt 4 .\) So sánh A với \(\sqrt 2 \)
\[A = \sqrt {16} - \sqrt {25} + \sqrt 4 = 4 - 5 + 2 = 1 < \sqrt 2 \]. Vậy \(A < \sqrt 2 \)
b) Giải hệ phương trình: \(\left\{ \begin{array}{l}x - y = - 5\\2x + y = 11\end{array} \right.\)
\(\left\{ \begin{array}{l}x - y = - 5\\2x + y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 6\\x - y = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2 - y = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 7\end{array} \right.\)
Câu 2:
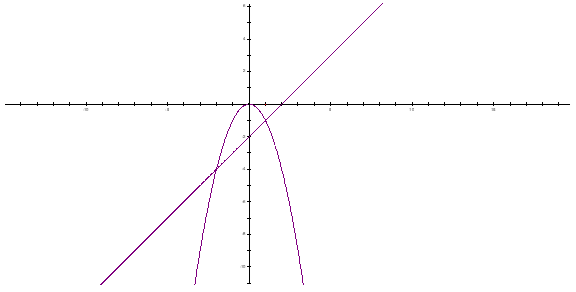
1. Cho Parabol \(\left( P \right):\,\,y = - {x^2}\) và đường thẳng \(\left( d \right):\,\,y = x - 2\)
a) Vẽ \(\left( P \right)\,\,v{\rm{\`a }}\,\,\left( d \right)\) trên cùng một mặt phẳng tọa độ \[{\rm{Ox}}y\].
b) Viết phương trình đường thẳng \(\left( {d'} \right)\)song song với \(\left( d \right)\) và tiếp xúc với \(\left( P \right)\).
2. Cho phương trình \({x^2} - 4x + m = 0\) (m là tham số)
a) Biết phương trình có một nghiệm bằng \( - 1\). Tính nghiệm còn lại.
b) Xác định m để phương trình có hai nghiệm \({x_1},\,{x_2}\) thỏa mãn \(\left( {3{x_1} + 1} \right)\left( {3{x_2} + 1} \right) = 4\)
1.
a) \(\left( P \right):\,\,y = - {x^2}\)
\(\left( d \right):\,\,y = x - 2\)
\(x = 0 \Rightarrow y = - 2:\,\,\,\,\,\,\left( {0; - 2} \right)\)
\(y = 0 \Rightarrow x = 2:\,\,\,\,\,\,\left( {2;0} \right)\)
b) Phương trình đường thẳng \(\left( {d'} \right)\) có dạng \(y = {\rm{ax}} + b\)
\(\left( {d'} \right)\)//\(\left( d \right):y = x - 2 \Rightarrow a = 1;\,\,b \ne - 2\)
Phương trình hoành độ giao điểm của \(\left( P \right)\,v{\rm{\`a }}\,\left( {d'} \right)\)là \( - {x^2} = x + b \Leftrightarrow {x^2} + x + b = 0\,\,\left( * \right)\)
PT \(\left( * \right)\) có \(\Delta = 1 - 4b\).
\(\left( P \right)\,v{\rm{\`a }}\,\left( {d'} \right)\)tiếp xúc nhau khi PT \(\left( * \right)\) có nghiệm kép \( \Leftrightarrow \Delta = 0 \Leftrightarrow 1 - 4b = 0 \Leftrightarrow b = \frac{1}{4}\) (nhận).
Vậy PT đường thẳng \(\left( {d'} \right)\,\,l{\rm{\`a }}:\,y = x + \frac{1}{4}\)
2.
a) PT \({x^2} - 4x + m = 0\)có một nghiệm bằng \( - 1\)\( \Rightarrow a - b + c = 0 \Rightarrow 1 + 4 + m = 0 \Rightarrow m = - 5\).
Nghiệm còn lại của PT là \( - \frac{c}{a} = - \frac{m}{1} = - \frac{{ - 5}}{1} = 5\)
b) ĐK \(\Delta ' = {\left( { - 2} \right)^2} - m \ge 0 \Leftrightarrow m \le 4\)
Áp dụng định lí Vi et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4\\{x_1}{x_2} = m\end{array} \right.\)
\(\begin{array}{l}\left( {3{x_1} + 1} \right)\left( {3{x_2} + 1} \right) = 4 \Rightarrow 9{x_1}{x_2} + 3\left( {{x_1} + {x_2}} \right) + 1 = 4\\ \Rightarrow 9m + 3.4 + 1 = 4 \Rightarrow m = - 1\,\left( {tm} \right)\end{array}\)
Vậy \(m = - 1\) là giá trị cần tìm.
Câu 3:
Một đội công nhân đặt kế hoạch sản xuất 250 sản phẩm. Trong 4 ngày đầu, họ thực hiện đúng kế hoạch. Mỗi ngày sau đó, họ đều vượt mức 5 sản phẩm nên đã hoàn thành công việc sớm hơn 1 ngày so với dự định. Hỏi theo kế hoạch, mỗi ngày đội công nhân đó làm được bao nhiêu sản phẩm? Biết rằng năng suất làm việc của mỗi công nhân là như nhau.
Gọi số sản phẩm mỗi ngày đội công nhân đó làm theo kế hoạch là x(sp).
ĐK \(x > 0;\,x \in Z\)
Khi đó, số sản phẩm mỗi ngày đội công nhân đó làm trong thực tế là \(x + 5\,\left( {sp} \right)\)
Thời gian hoàn thành công việc theo kế hoạch là \(\frac{{250}}{x}\,\)(ngày)
Số sản phẩm làm được trong 4 ngày đầu là: \(4x\,\left( {sp} \right)\)
Số sản phẩm còn lại phải làm là \(250 - 4x\,\left( {sp} \right)\)
Thời gian làm \(250 - 4x\,\left( {sp} \right)\)còn lại là \(\frac{{250 - 4x}}{{x + 5}}\) (ngày).
Theo bài toán ta có PT: \(\frac{{250}}{x}\, = 4 + \frac{{250 - 4x}}{{x + 5}} + 1\)
Giải PT này ta được: \({x_1} = 25\)(nhận)
\({x_2} = - 50\)(loại)
Vậy số sản phẩm mỗi ngày đội công nhân đó làm theo kế hoạch là 25 sản phẩm.
Câu 4:
Cho tam giác nhọn ABC (AB<AC), đường cao AH, nội tiếp đường tròn (O). Gọi D và E thứ tự là hình chiếu vuông góc của H lên AB và AC.
a) Chứng minh các tứ giác AEHD và BDEC nội tiếp được đường tròn.
b) Vẽ đường kính AF của đường tròn (O). Chứng minh \(BC = \sqrt {AB.BD} + \sqrt {AC.CE} \) và AF vuông góc với DE.
c) Gọi O’ là tâm đường tròn ngoại tiếp tam giác BDE. Chứng minh O’ là trung điểm của HF.
d) Tính bán kính đường trò (O’) biết \(BC = 8cm,\,\,DE = 6cm,\,\,{\rm{A}}F = 10cm.\)
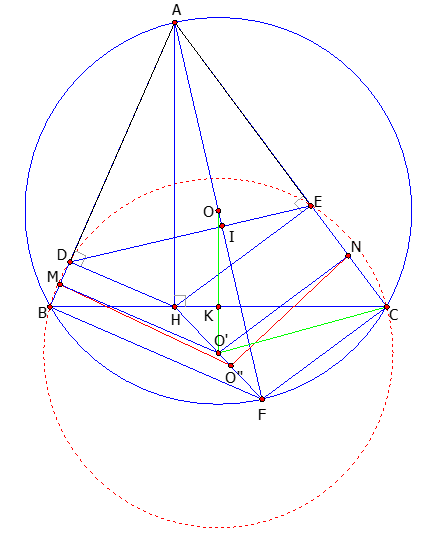
a) Tứ giác AEHD có \(\widehat {ADH} + \widehat {AEH} = {90^0} + {90^0} = {180^0} \Rightarrow \)Tứ giác AEHD nội tiếp được đường tròn đường kính AH.
Tứ giác AEHD (cmt) \(\widehat {ADE} = \widehat {AHE\,}\left( 1 \right)\)(cùng chắn ). Dễ thấy \(\widehat {ACH} = \widehat {AHE\,}\left( 2 \right)\) (cùng phụ \(\widehat {HAE}\)).
Từ (1) và (2) suy ra \(\widehat {ADE} = \widehat {ACH\,}\)nên tứ giác BDEC nội tiếp được đường tròn.
b) Áp dụng hệ thức lượng trong hai tam giác vuông AHB và AHC ta có:
\(\begin{array}{l}B{H^2} = AB.BD \Rightarrow BH = \sqrt {AB.BD} \\H{B^2} = AC.CE \Rightarrow HB = \sqrt {AC.CE} \end{array}\)
Do đó \(BC = BH + HC = \sqrt {AB.BD} + \sqrt {AC.CE} \)
Nối FB, FC. Gọi I là giao điểm của AF và DE.
Ta có \(\widehat {ADE} = \widehat {ACH\,}\) (cmt) và \(\widehat {AFB} = \widehat {ACH\,}\)(cùng chắn ) suy ra \(\widehat {ADE} = \widehat {AFB\,}\)nên tứ giác BDIF nội tiếp được đường tròn\( \Rightarrow \widehat {D{\rm{I}}F} + \widehat {DBF} = {180^0} \Rightarrow \widehat {D{\rm{I}}F} = {180^0} - \widehat {DBF} = {180^0} - {90^0} = {90^0}\). Vậy \[{\rm{A}}F \bot DE\]
c) Gọi M,N,O’’ lần lượt là trung điểm của BD,EC,HF.
– Ta chứng minh được MO’’ và NO’’ lần lượt là đường trung bình của các hình thang BDHF và CEHF\( \Rightarrow MO''//DH\left( 3 \right)\)và \( \Rightarrow NO''//EH\left( 4 \right)\)
– Vì tứ giác BDEC nội tiếp mà\(O'\)là tâm đường tròn ngoại tiếp tam giác BDE suy ra \(O'\)cũng là tâm đường tròn ngoại tiếp tứ giác BDEC\( \Rightarrow O'\) thuộc đường trung trực của BD . Suy ra MO’ là trung trực của BD do đó
\(MO' \bot BD\) lại có \(DH \bot BD\) \( \Rightarrow MO'//DH\left( 5 \right)\).
Tương tự ta có \(NO'//EH\left( 6 \right)\)
Từ (3) và (5) suy ra MO’’ và MO’ là hai tia trùng nhau
Từ (4) và (6) suy ra NO’’ và NO’ là hai tia trùng nhau
Do đó O’ trùng O”. Mà O’’ là trung điểm của HF nên O’ cũng là trung điểm của HF.
d) Trong \(\Delta ABC\) ta có \(\frac{{BC}}{{SinA}} = {\rm{A}}F \Rightarrow SinA = \frac{{BC}}{{{\rm{A}}F}} = \frac{8}{{10}} = \frac{4}{5}\)
Trong \(\Delta ADE\) ta có \(\frac{{DE}}{{SinA}} = {\rm{AH}} \Rightarrow AH = \frac{6}{{\frac{4}{5}}} = 7,5\left( {cm} \right)\)
Vì O’ và O lần lượt là trung điểm của HF và AF nên OO’ là đường trung bình của tam giác AHF\( \Rightarrow {\rm{OO' = }}\frac{{AH}}{2} = \frac{{7,5}}{2} = 3,75\left( {cm} \right)\)
Gọi K là giao điểm của OO’ và BC dễ thấy \[{\rm{OO}}' \bot BC\] tại trung điểm K của BC. Áp dụng định lí Pytago vào tam giác vuông OKC ta tính được \(OK = \sqrt {O{C^2} - K{C^2}} = \sqrt {{5^2} - {4^2}} = 3\left( {cm} \right)\)
Ta có \(KO' = {\rm{OO}}' - OK = 3,75 - 3 = 0,75\left( {cm} \right)\)
Áp dụng định lí Pytago vào tam giác vuông O’KC ta tính được \(O'C = \sqrt {O'{K^2} + K{C^2}} = \sqrt {{{0,75}^2} + {4^2}} = \frac{{\sqrt {265} }}{4}\left( {cm} \right)\)
Vậy bán kính đường trò (O’) là \(\frac{{\sqrt {265} }}{4}\left( {cm} \right)\).
Câu 5:
Cho hình vuông ABCD.
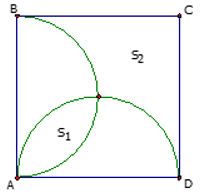
Gọi \({S_1}\) là diện tích phần giao của hai nửa đường tròn đường kính AB và AD. \({S_2}\) là diện tích phần còn lại của hình vuông nằm ngoài hai nửa đường trong nói trên (như hình vẽ trên).Tính \(\frac{{{S_1}}}{{{S_2}}}\).
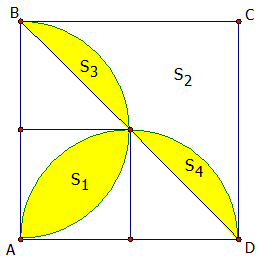
Gọi a là cạnh hình vuông ABCD. Ta cm được:
\({S_3} = {S_4} = \frac{{{{\left( {\frac{a}{2}} \right)}^2}.\pi .90}}{{360}} - \frac{1}{2} \cdot {\left( {\frac{a}{2}} \right)^2} = \frac{{{a^2}}}{4}\left( {\frac{\pi }{4} - \frac{1}{2}} \right)\)
\({S_1} = {S_3} + {S_4} = \frac{{{a^2}}}{4}\left( {\frac{\pi }{4} - \frac{1}{2}} \right) + \frac{{{a^2}}}{4}\left( {\frac{\pi }{4} - \frac{1}{2}} \right) = \frac{{{a^2}}}{2}\left( {\frac{\pi }{4} - \frac{1}{2}} \right)\)
\({S_2} = \frac{1}{2}{a^2} - \frac{{{a^2}}}{2}\left( {\frac{\pi }{4} - \frac{1}{2}} \right) = \frac{{{a^2}}}{2}\left( {\frac{3}{2} - \frac{\pi }{4}} \right)\)
Do đó \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{{{a^2}}}{2}\left( {\frac{\pi }{4} - \frac{1}{2}} \right)}}{{\frac{{{a^2}}}{2}\left( {\frac{3}{2} - \frac{\pi }{4}} \right)}} = \frac{{\pi - 2}}{{6 - \pi }}\).
