Trắc nghiệm Chuyên đề toán 9 Chuyên đề 7: Tứ giác ngoại tiếp, Đường tròn nội tiếp có đáp án
Trắc nghiệm Chuyên đề toán 9 Chuyên đề 7: Tứ giác ngoại tiếp, Đường tròn nội tiếp có đáp án
-
442 lượt thi
-
8 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Chứng minh định lí: “Nếu một tứ giác ABCD có tổng các cạnh đối bằng nhau AB+CD=BC+AD thì tứ giác đó ngoại tiếp được một đường tròn” bằng cách chứng minh các tia phân giác của bốn góc A,B,C,D cùng gặp nhau tại một điểm.
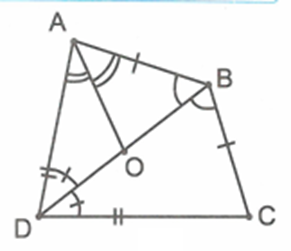
Ta chỉ cần chứng minh các tia phân giác của ba góc A,B,D gặp nhau tại một điểm. Xét hai trường hợp:
Trường hợp 1: Nếu AB=BC thì từ giả thiết suy ra CD=AD.
Xét ΔABD và ΔCBD có AB=BC, AD=DC và BD chung nên ΔABD=ΔCBD(c.c.c).
Do đó BD là đường phân giác của các góc B và D.
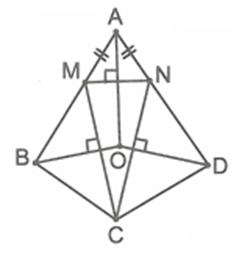
Gọi O là giao điểm của tia phân giác góc A với BD. Suy ra BO,DO là các tia phân giác của các góc B và D.
Trường hợp 2: Nếu AB≠BC, giả sử AB>BC, suy ra DA>DC.
Lấy điểm M trên AB, điểm N trên AD sao cho BM=BC,DN=DC.
Từ giả thiết suy ra AM=AN. Các đường phân giác của các góc A,B,D chính là các đường trung trực của tam giác CMN nên chúng gặp nhau tại một điểm O.
Vậy điểm O là tâm của đường tròn nội tiếp tứ giác ABCD.
Câu 2:
Cho đường tròn (O) nội tiếp tam giác ABC. D,E,F lần lượt là các tiếp điểm AB,BC,CA với (O).
Chứng minh rằng 2AD=AB+AC−BC.
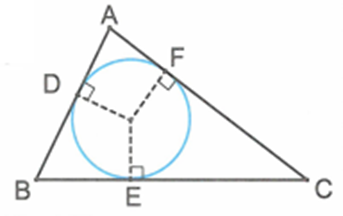
Vì (O) nội tiếp tam giác ABC nên các cạnh AB,BC,AC là các tiếp tuyến của đường tròn (O).
Theo tính chất của hai tiếp tuyến cắt nhau, ta có:
AD=AF,BD=BE,CE=CF.
Khi đó VP=AB+AC−BC
=(AD+BD)+(CF+FA)−(BE+CE)=AD+AF=2AD=VT.
Vậy 2AD=AB+AC−BC.
Câu 3:
Cho đường tròn (O) nội tiếp tam giác ABC. D,E,F lần lượt là các tiếp điểm AB,BC,CA với (O).
Tìm các hệ thức tương tự hệ thức ở bài trước.
Chứng minh tương tự câu a) ta cũng có các hệ thức sau:
2BD=2BE=AB+BC−AC;2CE=2CF=BC+AC−AB
Ví dụ 3: Cho hình thang ABCD vuông tại hai đỉnh A và D, ngoại tiếp đường tròn (O).
Tìm độ dài các cạnh AB và CD, biết rằng OB=6cm và OC=8cm.
Giải chi tiết
Do ABCD ngoại tiếp đường tròn (O) nên các cạnh của hình thang ABCD là tiếp tuyến của (O).
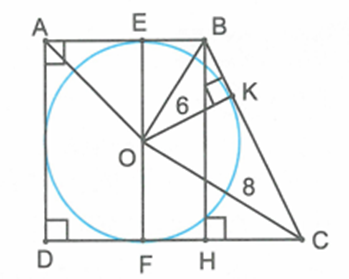
Theo tính chất của hai tiếp tuyến cắt nhau suy ra BO và CO lần lượt là tia phân giác của góc ^ABC,^BCD.
Xét ΔBOC có: ^OBC+^OCB=^ABC+^BCD2=180∘2=90∘.
Suy ra ΔBOC vuông O. Áp dụng định lí Pitago trong tam giác vuông này ta có:
BC2=OB2+OC2=62+82=100⇒BC=10cm.
Giả sử đường tròn (O) tiếp xúc với BC tại K, suy ra OK⊥BC.
Áp dụng hệ thức lượng trong tam giác vuông OBC, với OK là đường cao, ta có:
1OK2=1OB2+1OC2=162+182=25576⇒OK=245cm.
Gọi E,F lần lượt là tiếp điểm của AB và CD với đường tròn (O).
Suy ra OE=OK=245 (bán kính đường tròn (O)).
Kẻ BH⊥CD(H∈CD). Ta thấy: BH=EF=2OK=485cm.
Tương tự, áp dụng định lí Pitago trong tam giác vuông HBC ta được HC=145cm.
Ta có OE⊥AB (do AB là tiếp tuyến của (O)). Mặt khác AO là tia phân giác của góc ^DAB
⇒^OAE=45∘.
Suy ra tam giác AOE vuông cân ⇒AE=OE=245cm.
Áp dụng định lí Pitago trong tam giác vuông OEB ta được BE=185cm.
Vậy AB=AE+EB=245+185=425cm.
CD=DH+HC=AB+HC=425+145=565cm.
Câu 4:
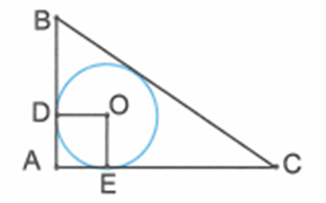
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB,AC lần lượt tại D,E.
Tứ giác ADOE là hình gì? Vì sao?
Đ/S: ADOE là hình vuông.
Câu 5:
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB,AC lần lượt tại D,E.
Tính bán kính của đường tròn (O) biết AB=3cm,AC=4cm.
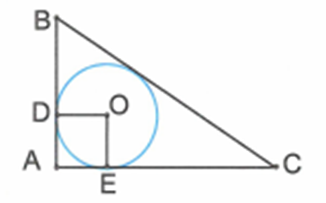
Áp dụng định lí Pitago trong tam giác vuông ABC, ta tính được BC=5cm.
Theo ví dụ 2, ta có: AD=AE=AB+AC−BC2=3+4−52=1cm.
Mà ADOE là hình vuông nên r=OD=OE=AD=AE=1cm.
Câu 6:
Cho đường tròn tâm O, các dây AB,CD vuông góc với nhau. Các tiếp tuyến với đường tròn tại A,B,C,D cắt nhau lần lượt tại E,F,G,H. Chứng minh rằng EFGH là tứ giác nội tiếp.
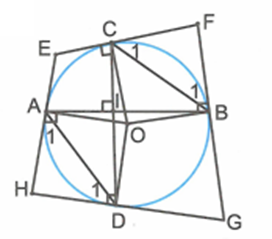
Gọi I là giao điểm của AB và CD. Góc ^BIC=90∘ và là góc có đỉnh I ở bên trong đường tròn nên .
Suy ra ^A1+^D1+^B1+^C1=180∘.
Ta có ˆF+ˆH=180∘−(^C1+^B1)+180∘−(^A1+^D1)=180∘.
Vậy EFGH là tứ giác nội tiếp.
Câu 7:
Làm tương tự ví dụ 3, ta tính được: r=4√5cm (với r là bán kính đường tròn nội tiếp hình thang ABCD), AB=6√5cm,CD=12√5cm.
Do đó diện tích hình thang ABCD là:
SABCD=(AB+CD).AD2=(6√5+12√5).8√52=360cm2
Câu 8:
Tứ giác ABCD ngoại tiếp đường tròn (O), đồng thời nội tiếp một đường tròn khác. AB=14cm,BC=18cm,CD=26cm. Gọi H là tiếp điểm của CD và đường tròn (O). Tính các độ dài HC,HD.
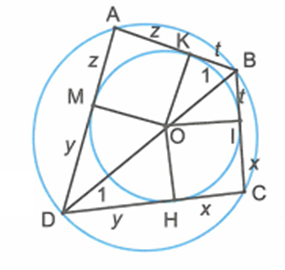
Gọi I,K,M là tiếp điểm của đường tròn (O) trên các cạnh BC,AB,AD và r là bán kính đường tròn (O).
Đặt CH=CI=x,DH=DM=y,AM=AK=z,BI=BK=t.
Do tứ giác ABCD ngoại tiếp đường tròn (O) nên:
AB+CD=AD+BC⇒AD=AB+CD−BC=14+26−18=22cm.
Lại có tứ giác ABCD là tứ giác nội tiếp nên
^ABC+^ADC=180∘⇔2(^B1+^D1)=180∘
⇔^B1+^D1=90∘⇒^B1=^HOD (vì cùng phụ với góc ^D1).
Ta có ΔKBO∼ΔHOD(g.g)⇒KBOH=OKHD⇔tr=ry⇔r2=yt.
Tương tự r2=xz. Do đó xz=yt. Suy ra xy=tz=18−x22−y=1822.
Từ đó ta tính được 11x=9y. Suy ra x=11,7 và y=14,3.
