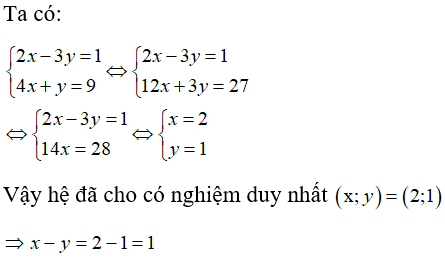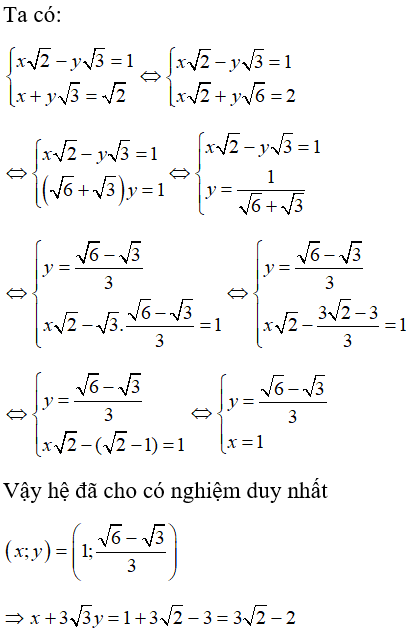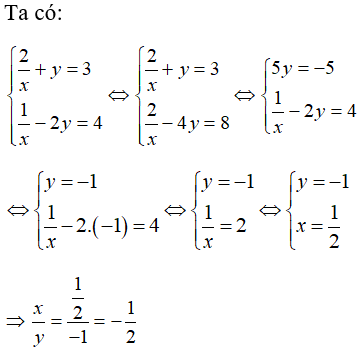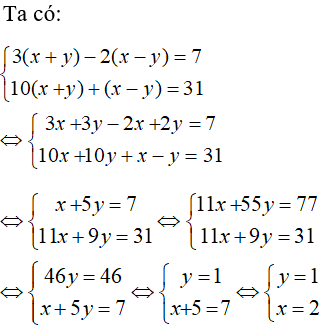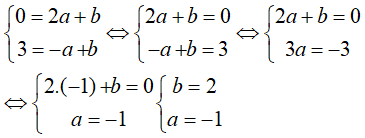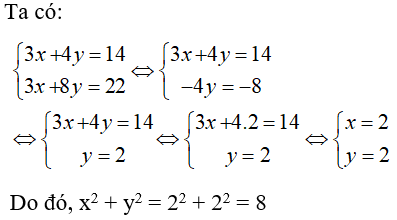Trắc nghiệm Toán lớp 9 Bài 4 (có đáp án): Giải hệ phương trình bằng phương pháp cộng đại số
Trắc nghiệm Toán 9 Bài 4 (có đáp án): Giải hệ phương trình bằng phương pháp cộng đại số
-
882 lượt thi
-
17 câu hỏi
-
10 phút
Danh sách câu hỏi
Câu 4:
Cho hệ phương trình . Biết nghiệm của hệ phương trình (x; y) , tính x.y
Đáp án B

Suy ra x.y = 1.0 = 0
Câu 5:
Cho hệ phương trình . Biết nghiệm của hệ phương trình là (x; y), tính x/y
Đáp án C
Câu 7:
Xác định hệ số a và b để đồ thị hàm số y = ax + b đi qua điểm A(2; 0) và B (-1; 3) ?
Đáp án B
Do đồ thị hàm số đã cho đi qua hai điểm A và B nên ta có:
Câu 11:
Tìm a, b để hệ phương trình có nghiệm là (3; −4)
Thay x = 3; y = −4 vào hệ phương trình ta được
Vậy a = ; b = 1
Đáp án: A
Câu 12:
Tìm a, b để hệ phương trình có nghiệm là (2; −3)
Thay x = 2; y = −3 vào hệ phương trình ta được:
Vậy a = 1; b =
Đáp án: D
Câu 13:
Nghiệm (x; y) của hệ phương trình có tính chất là:
Điều kiện: x ≥ 0; x ≠ 49; y ≥ 0
Đặt ta được
Trả lại biến ta có
Vậy hệ phương trình có nghiệm (x; y) = (100; 0)
Đáp án: D
Câu 14:
Tìm các giá trị của m để nghiệm của hệ phương trình: cũng là nghiệm của phương trình 6mx – 5y = 2m – 66
Ta có
Thay ; y = 7 vào phương trình 6mx – 5y = 2m – 66 ta được:
6m.− 5.7 = 2m – 66 31m = −31 m = −1
Đáp án: A
Câu 15:
Tìm các giá trị của m để nghiệm của hệ phương trình cũng là nghiệm của phương trình (m + 2)x + 7my = m – 225
Ta có
Thay x = 0; vào phương trình (m + 2)x + 7my = m – 225 ta được:
(m + 2).0 + 7m= m – 225m = 225m = 50
Đáp án: C
Câu 16:
Tìm a, b biết đường thẳng d: y = ax + b đi qua hai điểm A (−4; −2); B (2; 1)
Đường thẳng y = ax + b đi qua điểm A (−4; −2)−4a + b = −2 (1)
Đường thẳng y = ax + b đi qua điểm B (2; 1)2a + b = 1 (2)
Từ (1) và (2) ta có hệ:
Vậy a =; b = 0
Đáp án: B
Câu 17:
Tìm a, b biết đường thẳng d: y = ax + b đi qua hai điểm ; B (0; 2)
Đường thẳng y = ax + b đi qua điểm
Đường thẳng y = ax + b đi qua điểm B (0; 2)0.a + b = 2 (2)
Từ (1) và (2) ta có hệ:
Vậy a = 0; b = 2
Đáp án: A