Bài tập theo tuần Toán 9 - Tuần 3
-
390 lượt thi
-
27 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 6:
Cho tam giác DEF vuông tại D, đường cao DH, đường trung tuyến DM, DF = 16cm, EF = 20cm, Tính:
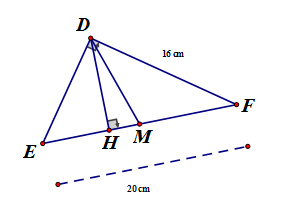
Áp dụng định lý Pytago vào hay
Áp dụng hệ thức lượng vào đường cao DH
Vì DM là đường trung tuyến trong vuông tại D
Vậy
Câu 7:
Cho tam giác ABC vuông tại A, đường cao AH, biết rằng BH = 25cm, CH = 144cm. Tính
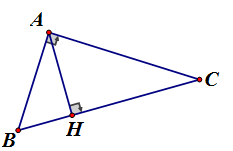
Áp dụng hệ thức lượng vào vuông tại A, đường cao AH ta có:
Vậy
Câu 8:
Một tam giác vuông có cạnh huyền là 5, và đường cao ứng với cạnh huyền là 2. Tính hai cạnh góc vuông.
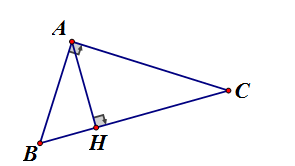
Theo bài BC = 5, AH = 2
Áp dụng hệ thức lượng vào vuông tại A, đường cao AH
Câu 9:
Cho tam giác nhọn ABC, AH là đường cao, D, E lần lượt là hình chiếu của H trên AB, AC. Chứng minh rằng:
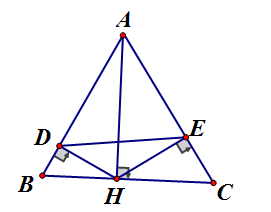
a) vuông tại H, HD là đường cao, áp dụng hệ thức lượng
chứng minh tương tự ta có
Từ (1) và (2) suy ra
b) Từ
Xét và có: chung
(hai góc tương ứng)
Câu 10:
Cho đoạn thẳng AB = 4cm, C là điểm di động sao cho BC = 3cm. Vẽ tam giác AMN vuông tại A có AC là đường cao. Xác định vị trí điểm C để đạt giá trị lớn nhất.
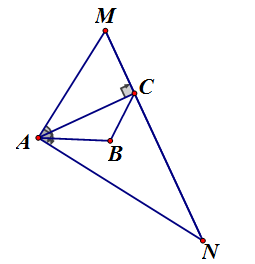
Xét vuông tại A, AC là đường cao (gt), áp dụng hệ thức lượng ta có:
Xét ba điểm A, B, C ta có:
Do vậy . Dấu "=" xảy ra nằm giữa hai điểm A và B
Vậy khi C nằm giữa A và B sao cho AB = 3cm thì lớn nhất
Câu 11:
Cho hình thoi ABCD với Tia Ax tạo với tia bằng và cắt cạnh BC tại M, cắt đường thẳng CD tại N.
Chứng minh rằng:
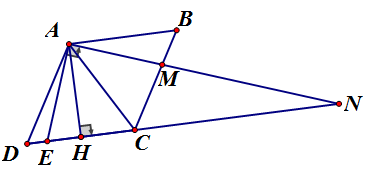
Vẽ
Ta có :
Xét và có: (tính chất hình thoi);
Do đó
vuông tại H có:
nên là nửa tam giác đều
có theo định lý pytago ta có:
có theo hệ thức về cạnh và đường cao trong tam giác vuông, ta có:
Câu 12:
Cho tam giác ABC vuông tại A, AH là đường cao. Cho biết BH = x, HC = y. Chứng minh rằng:
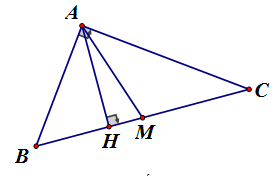
Vẽ đường trung tuyến AM của tam giác ABC
Tam giác ABC vuông tại A, AH là đường cao, áp dụng hệ thức lượng :
vuông tại A, AM là đường trung tuyến nên
Ta có:
