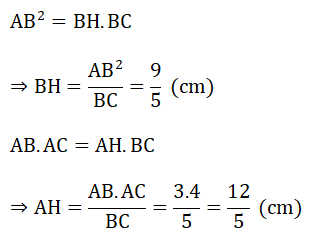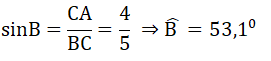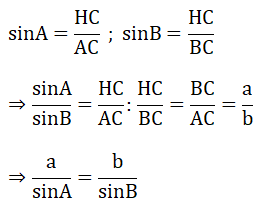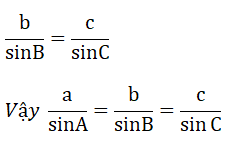14 câu hỏi trắc nghiệm thuộc Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án (Đề 2)

Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án

Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án (Đề 2)

2086 lượt thi
14 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Phần trắc nghiệm

Nội dung câu hỏi 1

Tam giác ABC vuông tại A, đường cao AH. Biết BH = 9cm, BC = 25cm, khi đó AB bằng:

A. 20cm

B. 15cm

C. 34cm

D. 25/9

Xem đáp án

Đáp án là B

Câu 2:

Giá trị của biểu thức sin $36^{0}$ - cos $54^{0}$ bằng:

A. 0

B. 2 sin $36^{0}$

C. 2 cos $54^{0}$

D. 1

Xem đáp án

Đáp án là A

Câu 3:

Tam giác DEF vuông tại D, biết DE = 25, góc E = $42^{0}$ , thì độ dài của cạnh EF bằng bao nhiêu?

A. 18,58

B. 22,51

C. 16,72

D. Một kết quả khác.

Xem đáp án

Đáp án là D

Câu 4:

Tam giác ABC vuông tại B, biết AB = 5, BC = 12 thì số đo của góc C bằng bao nhiêu?

A. $22^{0} 37'$

B. $20^{0} 48'$

C. $24^{0} 50'$

D. $23^{0} 10'$

Xem đáp án

Đáp án là A

Câu 5:

Tam giác OPQ vuông tại P, đường cao PH Biết OP = 8, PQ = 15 thì PH bằng bao nhiêu?

A. 7,58

B. 5,78

C. 7,06

D. 6,07

Xem đáp án

Đáp án là C

Câu 6:

Cho $α + β = 90^{0}$ , ta có:

A. $\sin α = \sin β$

B. $\tan α . c o t g α = \frac{\sqrt{2}}{2}$

C. $\sin^{2} α + \sin^{2} β = 1$

D. $\tan α = \frac{\cos β}{\cos α}$

Xem đáp án

Đáp án là D

Câu 7:

Phần tự luận

Nội dung câu hỏi 1

Đơn giản các biểu thức sau:

a) 1 - $\sin^{2} α$

Xem đáp án

a) $1 - \sin^{2} α = \cos^{2} α$

Câu 8:

Đơn giản các biểu thức sau:

b) sinα - sinα. $c o s^{2} α$

Xem đáp án

b) sinα - sinα. $c o s^{2} α$

= sinα (1 - $c o s^{2} α$ )

= sinα. $\sin^{2} α$

= $\sin^{3} α$

Câu 9:

Đơn giản các biểu thức sau:

c) $\sin^{4} α + \cos^{4} α + 2 \sin^{2} α c o s^{2} α$

Xem đáp án

c) $\sin^{4} α + \cos^{4} α + 2 \sin^{2} α c o s^{2} α$

= ${(\sin^{2} α + \cos^{2} α)}^{2}$

= 1

Câu 10:

Đơn giản các biểu thức sau:

$\sin^{2} 20^{0} + \cos^{2} 30^{0} - \sin^{2} 40^{0} - \sin^{2} 50^{0} + \cos^{2} 60^{0} + \sin^{2} 70^{0}$

Xem đáp án

$\sin^{2} 20^{0} + \cos^{2} 30^{0} - \sin^{2} 40^{0} - \sin^{2} 50^{0} + \cos^{2} 60^{0} + \sin^{2} 70^{0}$

$= \sin^{2} 20^{0} + \cos^{2} 30^{0} - \sin^{2} 40^{0} - c o s^{2} 40^{0} + \sin^{2} 30^{0} + \cos^{2} 20^{0}$

= (\sin^{2} 20^{0} + \cos^{2} 20^{0}) + (\cos^{2} 30^{0} + \sin^{2} 30^{0}) - (\sin^{2} 40^{0} + \cos^{2} 40^{0})

= 1 + 1 - 1

= 1

Câu 11:

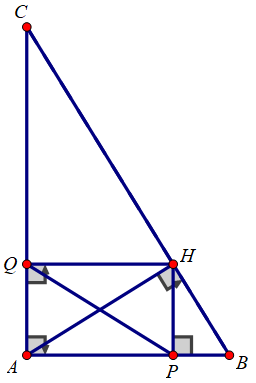
Cho tam giác ABC vuông tại A có AB = 3cm; BC = 5cm. Kẻ đường cao AH. Gọi P, Q lần lượt là hình chiếu của H trên AB và AC

a) Tính độ dài BH, CH, AH

Xem đáp án

a) Xét tam giác ABC vuông tại A có:

$A B^{2} + A C^{2} = B C^{2}$

Tam giác ABC vuông tại A có AH là đường cao nên ta có:

Ta có:

BH + CH = BC ⇒ CH = BC - BH = 5 - 9/5 = 16/5 (cm)

Câu 12:

Cho tam giác ABC vuông tại A có AB = 3cm; BC = 5cm. Kẻ đường cao AH. Gọi P, Q lần lượt là hình chiếu của H trên AB và AC

b) Tính số đo góc B, góc C. Tính PQ

Xem đáp án

b)Xét tam giác ABC vuông tại A có:

∠B + ∠C = $90^{0}$ ⇒ ∠C = $90^{0}$ - $53, 1^{0} = 36, 9^{0}$

Xét tứ giác APHQ có:

∠(PAQ) = ∠(AQH) = ∠(APH) = $90^{0}$

⇒ Tứ giác APHQ là hình chữ nhật

⇒ PQ = AH = 12/5 (cm)

Câu 13:

Cho tam giác ABC vuông tại A có AB = 3cm; BC = 5cm. Kẻ đường cao AH. Gọi P, Q lần lượt là hình chiếu của H trên AB và AC

c) Tính AP.BP + AQ.AC

Xem đáp án

c) Xét tam giác AHB vuông tại H có HP là đường cao nên

AP.BP = ${HP}^{2}$

Xét tam giác AHC có HQ là đường cao nên

AQ.AC = ${HQ}^{2}$

Khi đó: AP.BP + AQ.AC = ${HP}^{2}$ + ${HQ}^{2}$ = ${PQ}^{2}$ (ΔPHQ vuông tại H)

⇒ AP.BP + AQ.AC = ${(12 / 5)}^{2}$ = 5,76 cm

Câu 14:

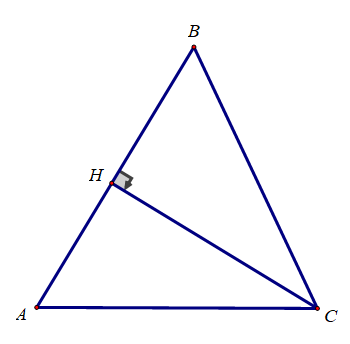
Cho tam giác ABC nhọn, độ dài các cạnh BC, CA, AB lần lượt là a, b, c. Chứng minh rằng:

$\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

Xem đáp án

Kẻ đường cao CH của tam giác ABC. Ta có:

Chứng minh tương tự ta có:

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án

Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương