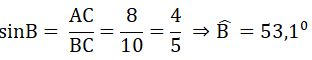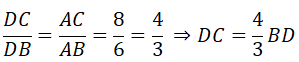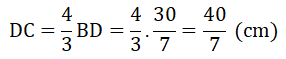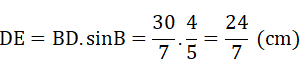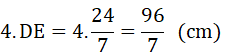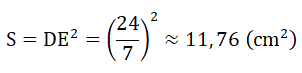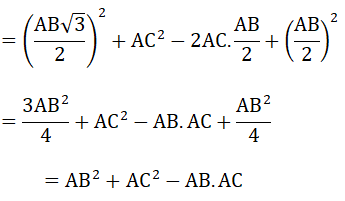Đề kiểm tra 1 tiết Toán 9 Chương 1 Hình học có đáp án (Đề 1)
-
2179 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phần trắc nghiệm
Nội dung câu hỏi 1
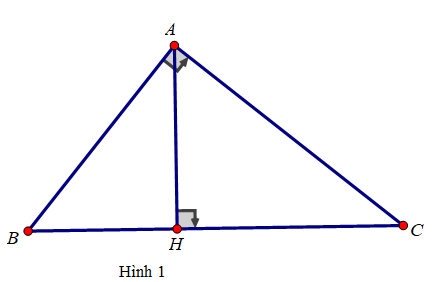
Dựa vào hình 1, hãy chọn câu đúng nhất:
Đáp án là B
Câu 4:
Cho tam giác ABC vuông tại A có ∠B =, AB = 6 cm. Kẻ đường cao AH. Độ dài đường cao AH là:
Đáp án là B
Câu 7:
Phần tự luận
Nội dung câu hỏi 1
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm
a) Tính BC, ∠B, ∠C
a) Xét tam giác ABC vuông tại A có:
= 100
⇒ BC = 10 (cm)
∠B + ∠C = ⇒ ∠C = =
Câu 8:
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm
b) Phân giác của góc A cắt BC tại D. Tính BD, CD
b) Do AD là tia phân giác của góc BAC, D ∈ BC nên ta có:
Mặt khác ta lại có:
DC + DB = BC ⇒ (4/3.BD) + BD = 10 ⇒ 7/3.BD = 10 ⇒ BD = 30/7 (cm)
Khi đó:
Câu 9:
Cho tam giác ABC vuông ở A, AB = 6cm, AC = 8cm
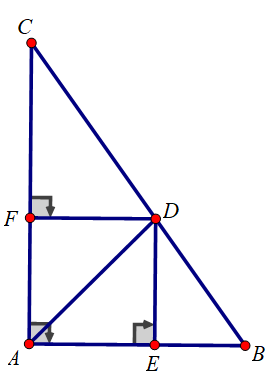
c) Từ D kẻ DE, DF vuông góc với AB, AC. Tứ giác AEDF là hình gì? Tính chu vi và diện tích của tứ giác AEDF
c) Xét tứ giác AEDF có:
∠(EAF) = ∠(AFD) = ∠(AED) =
⇒ Tứ giác AEDF là hình chữ nhật
Lại có: ΔAFD vuông tại F, có ∠(FAD) =
⇒ ΔAFD vuông cân tại F
⇒ AF = FD
⇒ tứ giác AEDF là hình vuông
Xét tam giác DEB vuông tại D có:
Chu vi hình vuông AEDF là:
Diện tích hình vuông AEDF là:
Câu 10:
Cho α là góc nhọn, sinα = 1/2.Tính cosα;tanα;cotα
Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có:
Câu 12:
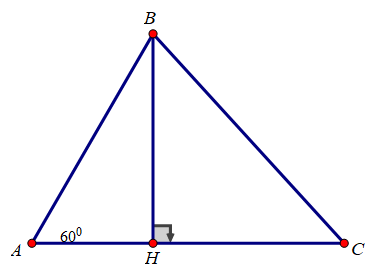
Cho tam giác ABC có ∠A = Chứng minh rằng:
- AB.AC
Kẻ đường cao BH
Xét tam giác ABH vuông tại H có ∠(BAC) =
BH = AB.sin A = AB.sin = (AB)/2
AH = AB.cos A = AB.cos = AB/2
Xét tam giác BHC vuông tại H có:
=
Vậy được điều phải chứng minh.