Bài tập theo tuần Toán 9 - Tuần 2
-
1458 lượt thi
-
46 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 8:
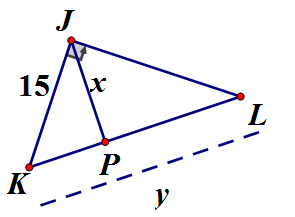

Áp dụng định lý Pytago vào có:
Áp dụng hệ thức lượng vào vuông tại J, JP đường cao
Vậy
Câu 9:
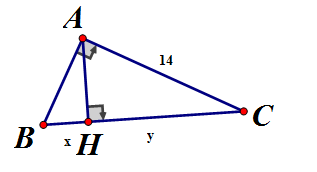
Cho vuông tại A, đường cao AH. Cho Tính
Áp dụng định lý Pytago vào vuông tại H, ta có:
Áp dụng hệ thức lượng vào đường cao AH ta có:
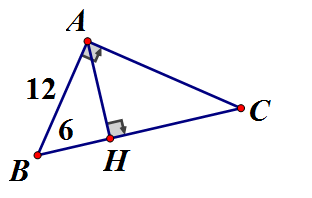
Áp dụng định lý Pytago vào vuông tại H, ta có:
Áp dụng hệ thức lượng vào vuông tại A, đường cao AH
Vậy
Câu 10:
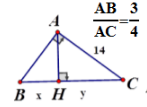
Cho một tam giác vuông. Biết tỉ số 2 cạnh của góc vuông là 3:4 và cạnh huyền là 125. Tính độ dài các cạnh góc vuông và hình chiếu của các cạnh góc vuông trên cạnh huyền
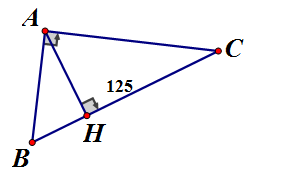
Vì
Áp dụng định lý Pytago vào vuông tại A, ta có:
Áp dụng hệ thức lượng vào vuông tại A, đường cao AH
hay
Câu 11:
Cho tam giác ABC vuông tại A. Biết rằng: đường cao AH = 30cm. Tính HB, HC.
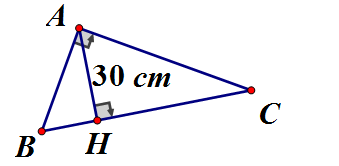
. Áp dụng hệ thức lượng vào vuông tại H, đường cao AH.
Áp dụng định lý Pytago vào
Vậy
Câu 44:
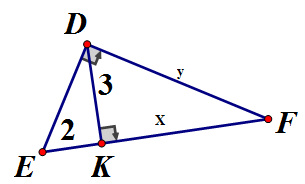

Áp dụng hệ thức lượng vào vuông tại D, đường cao DK
Vậy
Câu 46:
Cho vuông tại A, đường cao AH. Cho Tính

Áp dụng định lý Pytago vào vuông tại H, ta có:
Áp dụng hệ thức lượng vào vuông tại A, đường cao AH
Vậy