6 câu hỏi trắc nghiệm thuộc Bài tập theo tuần Toán 9 - Tuần 9 - Đề 4

Bài tập theo tuần Toán 9 - Tuần 9

Bài tập theo tuần Toán 9 - Tuần 9 - Đề 4

624 lượt thi
6 câu hỏi
30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tam giác ABC có $\hat{A} = 90^{0}$ , BC = 10 cm, $\hat{B} = 35^{0}$ . Giải tam giác vuông ABC.

Xem đáp án

Tam giác ABC có góc A = 90 độ, BC = 10 cm, góc B = 35 độ. Giải tam giác vuông ABC. (ảnh 1)

\begin{array}{l} \hat{C} = 90^{0} - 35^{0} = 55^{0} \\ A C = B C . \sin B = 10. \sin 35^{0} \approx 5, 74 (c m) \\ A B = B C . \cos B = 10. \cos 35^{0} \approx 8, 19 (c m) \end{array}

Vậy

\hat{C} = 55^{0}, A C = 5, 74 c m, A B = 8, 19 c m

Câu 2:

Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần

$\tan 27^{0}, \cot 49^{0}, \tan 80^{0}, \cot 23^{0}, \tan 25^{0}, \cot 50^{0}$

Xem đáp án

$\cot 49^{0} = \tan 41^{0}, \cot 23^{0} = \tan 67^{0}, \cot 50^{0} = \tan 40^{0}$

Vì $\tan 25^{0} < \tan 27^{0} < \tan 40^{0} < \tan 41^{0} < \tan 67^{0} < \tan 80^{0}$

Nên $\tan 25^{0} < \tan 27^{0} < \cot 50^{0} < \cot 49^{0} < \tan 23^{0} < \tan 80^{0}$

Câu 3:

Cho tam giác MNP vuông tại M, viết tỉ số lượng giác của góc N

Xem đáp án

\begin{array}{l} \sin N = \frac{M P}{N P} \cos N = \frac{M N}{N P} \\ \tan N = \frac{M P}{M N} \cot N = \frac{M N}{M P} \end{array}

Câu 4:

Tính góc nhọn $α$ biết

$S i n α = 0, 534 \cot α = 2, 654$

Xem đáp án

$\sin α = 0, 534 \Rightarrow α = 32^{0}$

Câu 5:

Cho

\cos α = \frac{\sqrt{5}}{3}

. Tính

\sin α; \tan α; \cot α

Xem đáp án

$\cot α = 2, 654 \Leftarrow \tan α = 0, 3768 \Rightarrow α \approx 21^{0}$

Câu 6:

Cho tam giác MNP có MN = 24 cm, NP = 32 cm, MP = 40 cm

a) Chứng minh tam giác MNP vuông

b) Vẽ đường cao NA, Tính NA, MA, AP

c) Kẻ đường phân giác NB. Tính chu vi tam giác NAB

Xem đáp án

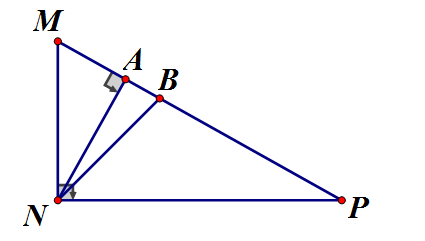
Cho tam giác MNP có MN = 24 cm, NP = 32 cm, MP = 40 cm a) Chứng minh tam giác MNP vuông (ảnh 1)

a) Ta có

M P^{2} = 40^{2} = 1600; M N^{2} + N P^{2} = 24^{2} + 32^{2} = 1600

\Rightarrow M P^{2} = M N^{2} + N P^{2}

\Rightarrow Δ M N P

vuông tại N (định lý Pytago đảo)

Áp dụng hệ thức lượng vào vuông $Δ M N P$ tại N, NA đường cao

$\Rightarrow \frac{1}{N A^{2}} = \frac{1}{N M^{2}} + \frac{1}{N P^{2}} = \frac{1}{24^{2}} + \frac{1}{32^{2}} = \frac{25}{9216} \Rightarrow N A = \sqrt{\frac{9216}{25}} = 19, 2 (c m)$

Áp dụng định lý Pytago vào các tam giác vuông MNA và PNA ta có:

$M A = \sqrt{M N^{2} - N A^{2}} = \sqrt{24^{2} - 19, 2^{2}} = 14, 4 (c m)$

$A P = \sqrt{N P^{2} - N A^{2}} = \sqrt{32^{2} - 19, 2^{2}} = 25, 6 (c m)$

Vậy

N A = 19, 2 c m; M A = 14, 4 c m; P A = 25, 6 c m

Vì NP là đường phân giác $Δ M N P$ $\Rightarrow \frac{M B}{B P} = \frac{M N}{P N}$ (tính chất đường phân giác trong tam giác)

$\Rightarrow \frac{M B}{M B + P B} = \frac{M N}{M N + P N} \Rightarrow \frac{M B}{M P} = \frac{M N}{M N + P N}$

hay $\frac{40}{M B} = \frac{24}{24 + 32} \Rightarrow M B = \frac{120}{7} (c m)$

$\Rightarrow A B = M B - M A = \frac{120}{7} - 14, 4 = \frac{96}{35} (c m)$

$N B = \sqrt{N A^{2} + A B^{2}}$ (áp dụng định lý Pytago vào $Δ N A B)$

$= \sqrt{19, 2^{2} + {(\frac{96}{35})}^{2}} = \frac{96 \sqrt{2}}{7} (c m)$

Chu vi tam giác NAB

$= N B + B A + A N = \frac{96 \sqrt{2}}{7} + \frac{96}{35} + 19, 2 \approx 41, 34 (c m)$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập theo tuần Toán 9 - Tuần 9

Bài tập theo tuần Toán 9 - Tuần 9 - Đề 4

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương