Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 14)
-
4801 lượt thi
-
5 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho biểu thức: B = (với x ≥ 0; x ≠ 4)
a) Rút gọn biểu thức B.
b) Tìm giá trị của x để biểu thức B có giá trị bằng 1.
a) Với x ≥ 0; x ≠ 4, ta có:
B =
=
=
= =
= .
Vậy với x ≥ 0; x ≠ 4, B = .
b) Với x ≥ 0; x ≠ 4. Ta có:
B = 1 Û = 1 suy ra − 1 = +2
Û =3Þ x = 9 (thỏa điều kiện x ≥ 0, x ≠ 4)
Vậy B có giá trị bằng 1 khi x = 9.
Câu 2:
Cho phương trình: x2 – mx + m – 2 = 0 (với m là tham số) (1)
a) Với giá trị nào của m để phương trình (1) có một nghiệm bằng 2, khi đó tìm nghiệm còn lại.
b) Chứng tỏ phương trình (1) luôn có 2 nghiệm phân biệt với mọi giá trị của m. Gọi x1, x2 là hai nghiệm của phương trình (1). Tìm giá trị của m để các nghiệm x1, x2 thỏa mãn: x1 + x2 + 2x1x2 = −1.
a) Phương trình (1) có một nghiệm bằng 2, ta thay x = 2 vào phương trình (1), ta được:
22 – m.2 + m – 2 = 0 Û 2 – m = 0 Û m = 2.
Có x1, x2 là các nghiệm của phương trình (1).
Theo hệ thức Vi-ét: x1x2 = = m – 2 hay x1x2 = 0.
Giả sử x1 = 2 ta có: 2.x2 = 0 Û x2 = 0
Vậy phương trình (1) có một nghiệm bằng 2 khi m = 2 và nghiệm còn lại bằng 0.
b) Xét ∆ = b2 – 4ac = (−m)2 – 4(m – 2)2 = m2 – 4m + 8 = (m – 2)2 + 4
Với mọi m, ta có (m – 2)2 ≥ 0 Û (m – 2)2 + 4 ≥ 4 > 0
Þ ∆ > 0.
Chứng tỏ phương trình (1) luôn có hai nghiệm phân biệt ∀m.
Theo hệ thức Vi-ét:
Nên x1 + x2 + 2x1x2 = −1 Û m + 2(m – 2) = −1 Û 3m – 4 = −1 Û m = 1.
Vậy phương trình (1) có hai nghiệm x1, x2 thỏa mãn: x1 + x2 + 2x1x2 = −1 thì m = 1.
Câu 3:
Cho hàm số y = x2 có đồ thị là parabol (P).
a) Tìm giá trị của m sao cho điểm C(−2; m) thuộc parabol (P).
b) Gọi A, B là các giao điểm của đường thẳng y = x + và parabol (P), biết hoành độ của điểm A nhỏ hơn hoành độ của điểm B. So sánh OB với ![]() .OA (với O là gốc tọa độ).
.OA (với O là gốc tọa độ).
a) Điểm C(−2; m) thuộc parabol (P) thì x = −2; y = m thỏa mãn hàm số y = x2.
Suy ra m = .(−2)2 = 2.
Vậy điểm C(−2; m) thuộc parabol (P) khi m = 2.
b) Hoành độ giao điểm của đường thẳng y = x + và parabol (P) là nghiệm của phương trình:
x2 = x + Û x2 – 2x − 3 = 0
Û x2 – 3x + x – 3 = 0
Û (x + 1)(x – 3) = 0
Vì hoành độ điểm A nhỏ hơn hoành độ điểm B, ta có:
Với x = x1 = -1 Þ y = (−1)2 = Þ A
Với x = x2 = 3 Þ y = .32 = ![]() Þ B
Þ B
Đường thẳng y = x + và parabol (P) cắt nhau tại A , B .
Ta có:
OA = Þ .OA = ;
OB = .
Vì 15 > 13 > 0 nên Þ > Þ .OA > OB.
Vậy .OA > OB.
Câu 4:
1. Cho nửa đường tròn tâm O đường kính AB, điểm C nằm giữa hai điểm O và A, đường thẳng vuông góc với AB tại C cắt nửa đường tròn tâm O tại I. Gọi K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn tâm O tại điểm M, tia BM cắt tia CI tại điểm D. Gọi N là giao điểm của AD và nửa đường tròn tâm O.
a) Chứng minh rằng: Tứ giác ACMD nội tiếp đường tròn.
b) Chứng minh rằng: CA.CB = CK.CD.
c) Chứng minh rằng: MA là phân giác .
d) Khi K di chuyển trên đoạn thẳng CI. Chứng minh rằng: Đường tròn ngoại tiếp tam giác AKD có tâm nằm trên một đường thẳng cố định.
2. Tính diện tích xung quanh của một hình nón, biết đường kính đáy là 40cm và độ dài đường sinh là 30cm (lấy p ≈ 3,14).
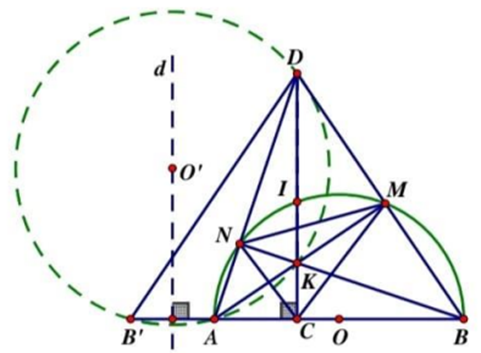
1.
a) Ta có = 90° (góc nội tiếp chắn nửa đường tròn tâm O).
Suy ra = 90° (kề bù với )
Có DC ^ AB Þ
Xét tứ giác ACMD có: = 90° (chứng minh trên).
Suy ra C, M cùng thuộc đường tròn đường kính AD (quỹ tích cung chứa góc)
Do đó tứ giác ACMB nội tiếp đường tròn đường kính AD.
b) Ta có tứ giác ACMB nội tiếp đường tròn đường kính AD
Suy ra (2 góc nội tiếp cùng chắn cung CM) hay
Xét ∆ACK và ∆DCB có:
Þ ∆ACK ∆DCB (g.g)
Þ Þ CA.CB = CD.CK
c) Ta có = 90° Þ AM ^ BD mà K là giao điểm của hai đường cao DC và AM.
Suy ra K là trực tâm của ∆ABD
Do đó BK ^ AD
Ta lại có = 90° (Góc nội tiếp chắn nửa đường tròn) Þ BN ^ AD.
Þ BK ≡ BN hay N, K, B thẳng hàng.
Þ KN ^ AD
Ta có tứ giác ACMD nội tiếp đường tròn
Þ (cùng chắn cung AC) (1)
Tứ giác KMDN có (tổng hai góc đối)
Suy ra tứ giác KMDN nội tiếp đường tròn đường kính DK
Do đó (cùng chắn cung KN) (2)
Từ (1) và (2) suy ra Þ MK là tia phân giác của .
d) Gọi B’ là điểm đối xứng với B qua DC Þ (tính chất đối xứng)
Ta có (hai góc đối đỉnh)
Ta có tứ giác BCKM nội tiếp ( )
Þ Þ
Þ Tứ giác AKDB’ nội tiếp đường tròn.
Gọi O’ là tâm đường tròn ngoại tiếp ∆AKD thì O’ cũng là tâm đường tròn ngoại tiếp tứ giác AKDB’
Nên O’ thuộc đường trung trực d của đoạn thẳng AB’.
Mà A, B, C cố định nên B’ cố định suy ra đường thẳng d cố định.
Vậy tâm O’ của đường tròn ngoại tiếp ∆AKD luôn nằm trên đường thẳng d là trung trực của đoạn thẳng AB’ cố định.
2. Diện tích xung quanh của hình nón là: Sxq = prl (với r là độ dài bán kính, l là độ dài đường sinh).
Có đườg kính d = 40 cm nên bán kính r = 20 cm
Có l = 30 cm
Sxq = 3,14 . 20 . 30 = 1884 (cm2).
Vậy diện tích xung quanh của hình nón là 1884 cm2.
Câu 5:
Cho a, b, c là các số dương thỏa mãn hệ thức: a + b + c = 6abc.
Chứng minh rằng: ≥ 2.
Áp dụng bất đẳng thức Cô-si cho 2 số dương, ta có:
Þ
≥ =
Vậy ≥
Dấu “=” xảy ra khi và chỉ khi a = b = c = .
