Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án (Đề 15)
-
4797 lượt thi
-
4 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho hàm số y = 2x2 có đồ thị (P).
a) Nêu điều kiện của x để hàm số đồng biến, nghịch biến.
b) Vẽ đồ thị (P).
a) Vì 2 > 0 nên hàm số đồng biến khi x > 0 và nghịch biến khi x < 0.
b) Bảng giá trị.
|
x |
−1 |
|
0 |
|
1 |
|
y = 2x2 |
2 |
|
0 |
|
2 |
Trên mặt phẳng tọa độ lấy các điểm: A(−1; 2); B; O(0; 0), C; D(1; 2).

Câu 2:
Cho phương trình x2 + 4x + m + 1 = 0 (1), với m là tham số.
a) Xác định các hệ số a, b, b’, c của phương trình (1).
b) Giải phương trình (1) khi m = −6.
c) Với giá trị nào của m thì phương trình (1) có nghiệm.
d) Tìm m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn x12 + x22 = 10.
a) Phương trình x2 + 4x + m + 1 = 0 có:
a = 1, b = 4, c = m + 1, b’ = = 2.
b) Thay m = −6 vào phương trình (1), ta được phương trình: x2 + 4x – 5 = 0
Û x2 – x + 5x – 5 = 0
Û x(x – 1) + 5(x – 1) = 0
Û (x – 1)(x + 5) = 0
Û
Û
Vậy tập nghiệm phương trình (1) là S = {1; −5}.
c) x2 + 4x + m + 1 = 0
∆ = b2 – 4ac = 42 – 4.1.(m + 1)
= 16 – 4m – 4 = 12 – 4m
Để phương trình (1) có nghiệm thì ∆ ≥ 0 Û 12 – 4m ≥ 0
Û 4m ≤ 12 Û m ≤ 3.
Vậy với m ≤ 3 thì phương trình (1) có nghiệm.
d) Theo định lý Vi-et, ta có:
S = x1 + x2 = = −4;
P = x1x2 = = m + 1.
Ta có: x12 + x22 = 10
Û (x1 + x2)2 – 2x1x2 = 10
Û (−4)2 – 2.(m + 1) = 10
Û 2(m + 1) = 6
Û m + 1 = 3 Û m = 2.
Vậy để phương trình (1) có hai nghiệm thỏa mãn yêu cầu bài toán thì m = 2.
Câu 3:
Cho tam giác ABC nhọn nội tiếp đường tròn (O), AB < AC. Các đường cao AD và BK cắt nhau tại H (D Î BC, K Î AC).
a) Chứng minh tứ giác CDHK nội tiếp được đường tròn.
b) Đường thẳng AD cắt đường tròn (O) tại E. Chứng minh .
c) Chứng minh BC là tia phân giác của .
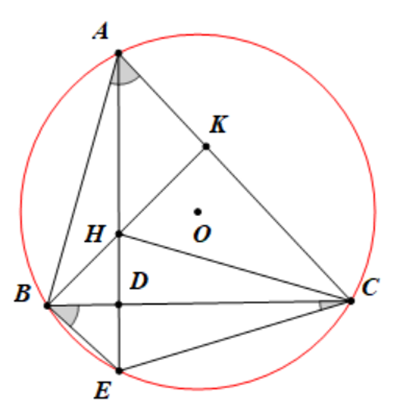
Ta có: = 90° (AD ^ BC, H Î AD)
= 90° (BK ^ AC, H Î BK)
Suy ra = 180°
Vậy tứ giác CDHK nội tiếp.
b) Ta có ∆ABC nội tiếp đường tròn tâm O nên A, B, C Î (O).
AD cắt đường tròn (O) tại E suy ra E Î (O).
Do đó tứ giác ABEC nội tiếp.
Vậy (hai góc cùng chắn cung CE).
c) Xét ∆ADC và ∆BKC, có:
chung
Do đó ∆ADC ∆BKC (g.g)
Suy ra (hai góc tương ứng)
Mà (cmt) nên
Do đó BC là tia phân giác của .
Câu 4:
Tính diện tích xung quanh của một hình trụ có bán kính đường tròn đáy 6cm, chiều cao 5 cm.
Diện tích xung quanh của một hình trụ là:
2p.5.6 = 60p (cm2)
Vậy diện tích xung quanh của hình trụ là 60p cm2.
