Trắc nghiệm Chuyên đề toán 9 Chuyên đề 2-2: Hàm số và đồ thị có đáp án
-
486 lượt thi
-
61 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Hàm số nghịch biến khi và đồng biến khi .
Vậy .
Câu 2:
Cho đường thẳng d: y = (m - 1)x + n . Tìm các giá trị của m và n để đường thẳng d đi qua điểm A(1;-1) và có hệ số góc bằng -3.
Đường thẳng d có hệ số góc bằng -3 nên .
Đường thẳng d đi qua điểm A(1;-1) nên
Vậy .Câu 3:
Theo giả thiết (D) đi qua hai điểm A(5;1) và B(-1;-1) nên ta có:
Thay vào phương trình của hàm số ta được: .
Vậy phương trình đường thẳng cần tìm là .
Câu 4:
Hàm số đồng biến trên , với mọi m.
, với mọi m (luôn đúng).
Vậy với mọi giá trị của m thì hàm số luôn đồng biến trên R.
Câu 5:
Cho đường thẳng .
a) Khi m = 3, tìm a để điểm A(a;-4) thuộc đường thẳng (d).
a) Khi m = 3 để điểm A(a;-4) thuộc đường thẳng (d) thì .
Vậy a = -3
Câu 6:
b) Đường thẳng (d) cắt các trục tọa độ Ox, Oy lần lượt tại M và N thì và nên
Mà
Vậy .
Câu 7:
Bảng giá trị giữa x và y:
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
8 |
2 |
0 |
2 |
8 |
Đồ thị hàm số đã cho có dạng như hình vẽ.
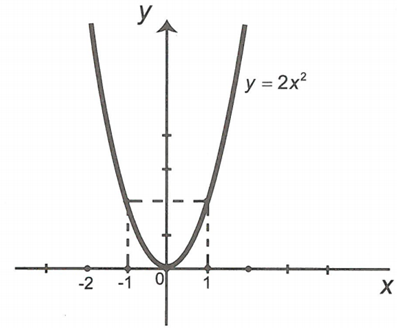
Câu 9:
b) Gọi A, B là giao điểm của đồ thị hàm số trên với trục tung và trục hoành. Tính diện tích tam giác OAB.
b) Ta có
Vậy .
Câu 10:
Cho parabol và đường thẳng .
a) Vẽ đồ thị .
a) Vẽ đồ thị
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
4 |
1 |
0 |
1 |
4 |
Đồ thị hàm số có dạng như hình vẽ.
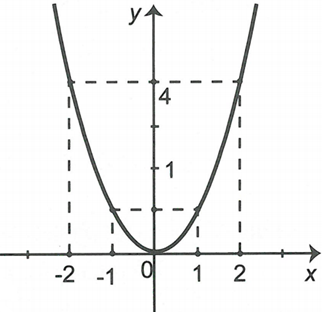
Câu 11:
b) Gọi phương trình đường thẳng có dạng: .
Vì song song với nên ta có:
Phương trình hoành độ giao điểm của và là:
(*)
Vì tiếp xúc với nên (*) có nghiệm kép (thoản mãn).
Vậy phương trình đường thẳng là: .
Câu 12:
Cho đường thẳng: (với m là tham số). Chứng minh rằng đường thẳng luôn đi qua một điểm cố định với mọi giá trị của m.
Giả sử là điểm cố định thuộc đường thẳng đã cho. Ta có:
với mọi m với mọi m
Vậy đường thẳng đã cho luôn đi qua điểm với mọi m.
Câu 13:
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng:
(với m là tham số khác 0).
Tìm điểm cố định mà đường thẳng luôn đi qua. Chứng minh rằng giao điểm của hai đường thẳng luôn thuộc một đường cố định.
Giả sử là điểm cố định mà đường thẳng luôn đi qua. Ta có:
với mọi m với mọi m
Vậy đường thẳng luôn đi qua điểm cố định.
Giả sử là giao điểm của và . Khi đó:
Nhân theo vế của (1) và (2) ta được:
Giả sử I(3;0) thuộc mặt phẳng tọa độ. Ta có không đổi.
Vậy N thuộc đường tròn tâm I bán kính .
Câu 14:
Trong mặt phẳng tọa độ Oxy, cho các đường thẳng có phương trình:
.
Tìm k để các đường thẳng trên đồng quy.
Tọa độ giao điểm của là nghiệm của hệ:
Do đó các đường thẳng trên đồng quy đi qua điểm
Vậy thì các đường thẳng đã cho đồng quy.
Câu 15:
Giả sử đường thẳng đi qua A(2;4) và B(-3;-1) có phương trình là y = ax + b.
Khi đó:
Suy ra phương trình đường thẳng đi qua A và B là .
Mà không thuộc đường thẳng (d) vì hay ba điểm A, B, C không thẳng hàng.
Chú ý: Ngoài ra, ta có thể chứng minh ba điểm A, B, C không thẳng hàng bằng cách chứng minh AB khác BC + AC hoặc BC khác AB + AC hoặc AC khác AB + BC.
Khoảng cách giữa hai điểm A và B là .
Khoảng cách giữa hai điểm B và C là .
Khoảng cách giữa hai điểm A và C là
Ta có: . Tương tự, ta có BC khác AB + AC và AC khác AB + BC. Suy ra ba điểm A, B, C không thẳng hàng.
Tương tự, để chứng minh ba điểm A, B, C thẳng hàng ta có thể chứng minh AB = BC + AC (chứng minh tổng hai đoạn bằng độ dài một đoạn còn lại).
Câu 16:
Tìm giá trị của m để hai đường thẳng và cắt nhau tại một điểm M thuộc đường thẳng .
Để hai đường thẳng cắt nhau thì luôn thỏa mãn với mọi m.
Tọa độ giao điểm M của là nghiệm của hệ phương trình:
Vì M thuộc đường thẳng (d) nên:
Vậy với m = 0 hoặc m = -1 thì hai đường thẳng và cắt nhau tại một điểm M thuộc đường thẳng (d).
Câu 17:
Trong mặt phẳng tọa độ Oxy, cho parabol (P) có phương trình và hai điểm A, B thuộc (P) có hoành độ lần lượt là .
a) Tìm tọa độ của hai điểm A, B.
a) Vì A, B thuộc (P) nên:
Vậy .
Câu 18:
b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.
Câu 19:
c) Tính khoảng cách từ điểm O (gốc tọa độ) tới đường thẳng (d).
c) (d) cắt Oy tại điểm C(0;1) và cắt trục Ox tại điểm D(-2;0).
Ta có: OC = 1 và OD = 2. Gọi h là khoảng cách từ O tới d.
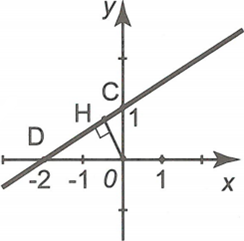
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông OCD
Ta có:
Câu 20:
Cho đường thẳng (với m là tham số). Tìm m để:
a) Khoảng cách từ gốc tọa độ O đến đường thẳng (d) bằng .
a) Cho x = 3 thì y = 3. Suy ra (d) cắt trục Oy tại điểm B(0;3)
Cho y = 0 thì . Suy ra (d) cắt trục Ox tại điểm
Ta có: . Gọi h là khoảng cách từ O đến đường thẳng (d).
Theo giả thiết,
Câu 21:
b) Ta thấy, khoảng cách từ O đến đường thẳng d đạt giá trị lớn nhất đạt giá trị nhỏ nhất.
Ta có: .
Đẳng thức xảy ra
Vậy
Câu 22:
Cho hai đường thẳng và . Tìm m để (d) và (d') song song với nhau.
Điều kiện để hai đồ thị song song là
Vậy m = -1 thì hai đường thẳng đã cho song song.
Câu 23:
Tìm giá trị của tham số k để đường thẳng cắt đường thẳng tại một điểm nằm trên trục hoành.
Ta thấy hai đường thẳng luôn cắt nhau:
+ Đường thẳng cắt trục hoành tại điểm A(2;0)
+ Đường thẳng cắt trục hoành tại điểm
+ Để hai đường thẳng cắt nhau tại một điểm trên trục hoành thì .
Vậy .
Câu 24:
Cho hai hàm số với và có đồ thị cắt nhau tại điểm . Tìm các giá trị của m để biểu thức đạt giá trị nhỏ nhất.
Với hai đồ thị cắt nhau tại điểm
Ta có:
Đặt ta được
Đẳng thức xảy ra
Vậy m = 0 thì biểu thức đạt giá trị nhỏ nhất.
Câu 25:
Cho hai hàm số và
a) Tìm tọa độ giao điểm M của hai đồ thị hàm số trên.
Câu 26:
b) Gọi N, P lần lượt là giao điểm của hai đồ thị trên với trục tung. Tính diện tích tam giác MNP.
b)
Gọi H là hình chiếu của M trên Oy.
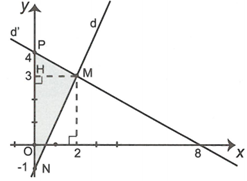
Ta có
Diện tích tam giác (đvdt).
Câu 27:
Xét phương trình hoành độ giao điểm của (P)và (d):
Thay x = 3 vào phương trình đường thẳng (d) ta được y = -9.
Vậy giao điểm của hai đồ thị là M(3;-9)
Câu 28:
Thay x = -1 và x = 2 vào phương trình y = x + 2 ta lần lượt được y = 1 và y = 4.
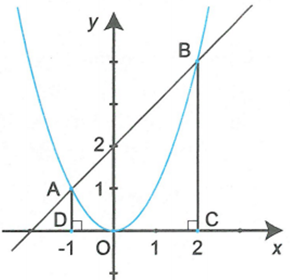
Vậy . Suy ra .
Tứ giác ABCD là hình thang vuông nên có diện tích là:
Câu 29:
Trên mặt phẳng tọa độ Oxy cho đường thẳng và parabol .
a) Tìm tọa độ các giao điểm của (d) và (P).
a) Phương trình hoành độ giao điểm của (d) và (P) là:
suy ra phương trình có 2 nghiệm phân biệt x = 2; x = -3
Với x = 2 thì y = 4, suy ra A(2;4).
Với x = -3 thì y = 9, suy ra B(-3;9).
Câu 30:
b) Gọi A, B là hai giao điểm của (d) và (P). Tính diện tích tam giác OAB.
b) Gọi lần lượt là hình chiếu của A và B xuống trục hoành.

Ta có:
Ta có: (đvdt)
(đvdt)
(đvdt)
Vậy diện tích tam giác OAB là: (đvdt).
Câu 31:
Trong mặt phẳng tọa độ Oxy, cho parabol và đường thẳng .
a) Với m = 3, tìm tọa độ giao điểm của (d) và (P).
Xét phương trình hoành độ giao điểm của (d) và (P):
(1)
a) Với thì phương trình (1) trở thành:
Thay lần lượt vào phương trình của parabol ta được .
Vậy với m = 3 thì (d) và (P) cắt nhau tại hai điểm phân biệt .
Câu 32:
b) Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ lần lượt là chiều dài và chiều rộng của hình chữ nhật có diện tích bằng .
b) Để cắt tại hai điểm phân biệt có hoành độ lần lượt là chiều dài và chiều rộng của hình chữ nhật có diện tích bằng thì phương trình (1) phải có hai nghiệm dương phân biệt và thỏa mãn .
Phương trình (1) có hai nghiệm dương phân biệt
Ta có:
Vậy là giá trị cần tìm.
Câu 33:
Trong mặt phẳng tọa độ Oxy cho đường thẳng và parabol .
a) Chứng minh (d) và (P) cắt nhau tại hai điểm phân biệt.
a) Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình:
(1)
Ta có:
Xét (vì ).
Do đó phương trình (1) luôn có hai nghiệm phân biệt. Vậy (d) và (P) cắt nhau tại hai điểm phân biệt với mọi m.
Câu 34:
b) Tìm tất cả các giá trị của m để (d) và (P) cắt nhau tại hai điểm phân biệt có hoành độ là các số nguyên.
b) Gọi là nghiệm của phương trình (1). Theo định lí Vi-ét:
Để mà nên hoặc hoặc hoặc
Suy ra
Vậy với m = 0 hoặc m = -4 thì (d) và (P) cắt nhau tại hai điểm phân biệt có hoành độ là các số nguyên.
Câu 35:
Cho parabol và đường thẳng (m là tham số).
a) Tìm m để (d) cắt (P) tại hai điểm phân biệt A, B.
a) Để (d) và (P) cắt nhau tại hai điểm phân biệt thì phương trình hoành độ giao điểm:
có hai nghiệm phân biệt
Câu 36:
b) Giả sử là hoành độ của A, B. Tìm m để .
b) Theo hệ thức Vi-ét ta có:
+ Xét m > 4 thì , do đó:
(loại vì m > 4)
+ Xét m < 0 thì , do đó:
Vậy
Câu 38:
Cho parabol và đường thẳng .
a) Vẽ parabol (P) và đường thẳng (d) trên cùng một mặt phẳng tọa độ Oxy.
a) HS tự làm.
Câu 39:
b) Tìm tọa độ giao điểm của parabol (P) và đường thẳng (d) bằng phép tính.
b) Phương trình hoành độ giao điểm của (d) và (P) là:
Vậy tọa độ giao điểm của (d) và (P) là .
Câu 40:
Cho parabol . Tìm a biết rằng parabol đi qua điểm . Vẽ với a vừa tìm được.
(P) đi qua điểm A(3;-3) nên ta có
Vậy
Câu 42:
b) Tìm tất cả các giá trị của tham số m để (d) cắt (P) tại hai điểm phân biệt.
b) Đáp số:
Câu 43:
Tìm tất cả các giá trị của tham số k để đường thẳng cắt đường thẳng tại một điểm nằm trên trục hoành.
Ta thấy hai đường thẳng luôn cắt nhau:
+ Đường thẳng cắt trục hoành tại điểm A(3;0).
+ Đường thẳng cắt trục hoành tại điểm B(k-2;0).
+ Để hai đường thẳng cắt nhau tại một điểm trên trục hoành thì .
Vậy k = 5.
Câu 44:
Để hàm số bậc nhất đồng biến trên R thì .
Câu 45:
Cho hai đường thẳng cắt nhau tại I. Tìm m để đường thẳng đi qua điểm I.
Tọa độ I là nghiệm của hệ
Do đi qua điểm I nên
Câu 46:
Cho đường thẳng (m là tham số).
a) Tìm m để đường thẳng vuông góc với đường thẳng .
a) Để đường thẳng vuông góc với đường thẳng thì
Câu 48:
Cho hàm số: y = mx + 1 (1), trong đó m là tham số.
a) Tìm m để đồ thị hàm số (1) đi qua điểm A(1;4). Với giá trị m vừa tìm được, hàm số (1) đồng biến hay nghịch biến trên R?
a) Ta có y = mx + 1 đi qua A(1;4) khi và chỉ khi 4 = m + 1 <=> m = 3.
Khi đó đường thẳng y = 3x + 1 đồng biến trên R.
Câu 49:
b) Ta có , đồ thị hàm số (1) song song với đường thẳng (d) khi
Vậy
Câu 50:
Cho hàm số bậc nhất (1). Hãy xác định hệ số a, biết rằng a > 0 và đồ thị của hàm số (1) cắt trục hoành và trục tung lần lượt tại hai điểm A, B sao cho OB = 2OA (với O là gốc tọa độ).
Ta có , để
Câu 51:
Trong mặt phẳng với hệ tọa độ Oxy, cho parabol và đường thẳng .
a) Vẽ đồ thị của (P).
a) HS tự vẽ.
Câu 52:
b) Gọi và lần lượt là các giao điểm của (d) và (P). Tính giá trị biểu thức .
b) Phương trình hoành độ giao điểm của (d) và (P) là:
Giao điểm của (d) và (P) là . Vậy
Câu 54:
b) Gọi A, B là các giao điểm của hai đồ thị (d) và (P). Biết rằng đơn vị đo trên các trục tọa độ là xentimét, tìm tất cả các điểm M trên tia Ox sao cho diện tích tam giác MAB bằng 30cm2.
b) Giao điểm của (d) và (P) là
Gọi thuộc tia . Gọi lần lượt là hình chiếu của A và B trên Ox.
Xét hai trường hợp: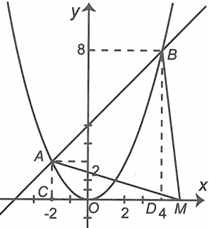
Suy ra (loại)
Trường hợp 2: M thuộc tia
Ta có:
Vậy
Câu 55:
Cho parabol và đường thẳng (m là tham số)
a) Chứng minh rằng với mọi m đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt.
a) Phương trình hoành độ giao điểm:
Ta có: với mọi m.
Vậy parabol luôn cắt đường thẳng tại hai điểm phân biệt.
Câu 56:
b) Tìm các giá trị của m để đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt thỏa mãn
b) Vì là nghiệm của phương trình (*) nên theo hệ thức Vi-ét ta có:
Mặt khác
Ta có:
Vậy .
Câu 57:
Trong mặt phẳng tọa độ Oxy, cho parabol và đường thẳng
a) Vẽ (d) và (P) trên cùng một mặt phẳng tọa độ khi m = 2.
a) HS tự làm.
Câu 58:
b) Định các giá trị của m để (d) cắt (P) tại hai điểm phân biệt A và B.
b) Phương trình hoành độ giao điểm của (d) và (P) là:
(d) cắt (P) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt
Câu 59:
c) Tìm giá trị của m để độ dài đoạn thẳng .
c) Giả sử , với là hai nghiệm của phương trình (1). Theo định lí Vi-ét có:
Ta có:
Theo giả thiết:
(thỏa mãn).
Câu 60:
Cho parabol và đường thẳng .
a) Xác định tọa độ giao điểm của (d) và (P) khi m = 0.
a) HS tự làm.
Câu 61:
b) Tìm m để (d) và (P) cắt nhau tại hai điểm phân biệt thỏa mãn .
b) Phương trình hoành độ giao điểm của (d) và (P) là:
(1)
Nhận thấy nên phương trình (1) có hai nghiệm .
(d) cắt (P) tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt
Để thì
Kết hợp với điều kiện (*) suy ra .

