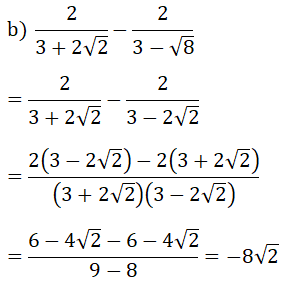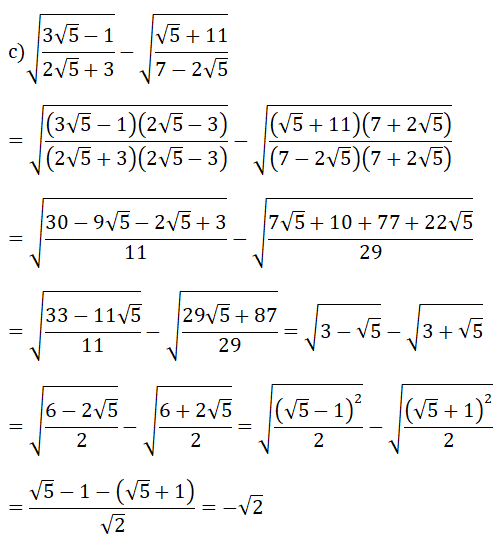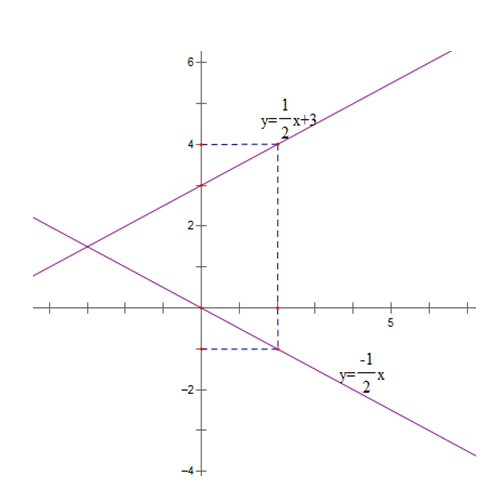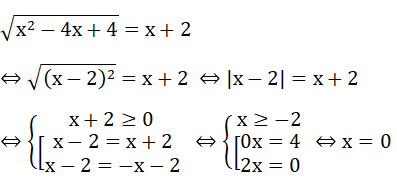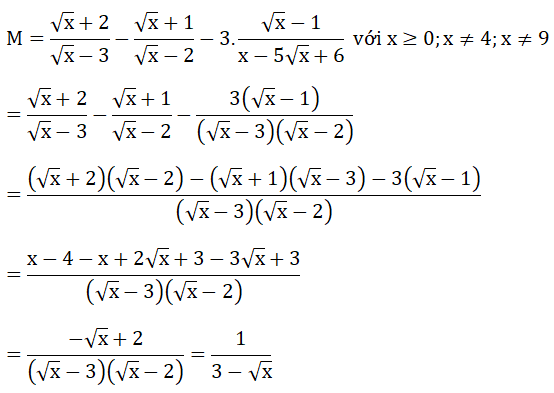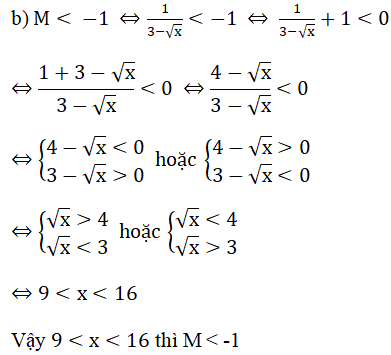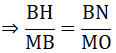Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án (Đề 1)
-
3098 lượt thi
-
12 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 4:
a) Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau:
a) Tập xác định của hàm số R
Bảng giá trị
| x | 0 | 2 |
| y = -1/2 x | 0 | - 1 |
| y = 1/2 x + 3 | 3 | 4 |
Câu 5:
Xác định b để đường thẳng () y = 2x + b cắt ( ) tại điểm có hoành độ và tung độ đối nhau.
b) Gọi A (m; - m) là tọa độ giao điểm của () và ()
Khi đó:
-m = 1/2 m + 3 ⇔ 3/2 m = 3 ⇔ m = 2
Vậy tọa độ giao điểm của và là (2; -2)
⇒ -2 = 2.2 + b ⇔ b = -6
Vậy b = - 6
Câu 9:
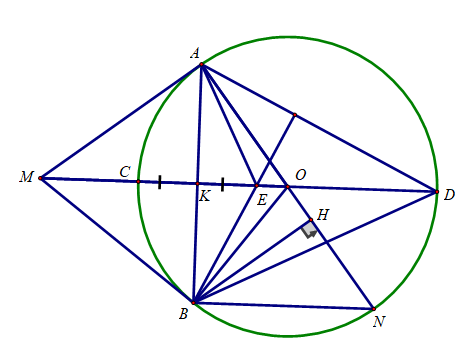
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
a) Chứng minh K là trung điểm của AB.
a) Ta có:
MA = MB ( tính chất 2 tiếp tuyến cắt nhau)
OA = OB ( cùng bằng bán kính đường tròn (O)
⇒ OM là đường trung trực của AB
OM ∩ AB = K ⇒ K là trung điểm của AB
Câu 10:
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
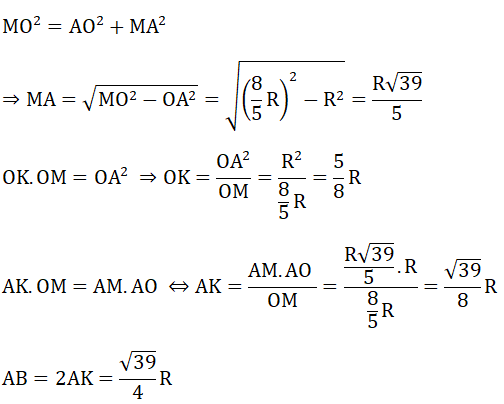
b) Tính MA, AB, OK theo R.
b) Tam giác MAO vuông tại A, AK là đường cao có:
Câu 11:
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO .
c) Ta có: ∠(ABN ) = (B thuộc đường tròn đường kính AN)
⇒ BN // MO ( cùng vuông góc với AB)
Do đó:
∠(AOM) = ∠(ANB) (đồng vị))
∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))
⇒ ∠(ANB) = ∠(BOM)
Xét ΔBHN và ΔMBO có:
∠(BHN) = ∠(MBO ) =
∠(ANB) = ∠(BOM)
⇒ ΔBHN ∼ ΔMBO (g.g)
Hay MB. BN = BH. MO
Câu 12:
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
d) Đường thẳng MO cắt đường tròn (O) tại C và D (C nằm giữa O và M). Gọi E là điểm đối xứng của C qua K. Chứng minh E là trực tâm của tam giác ABD.
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB