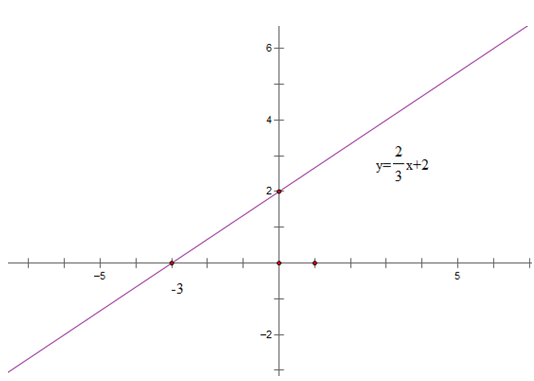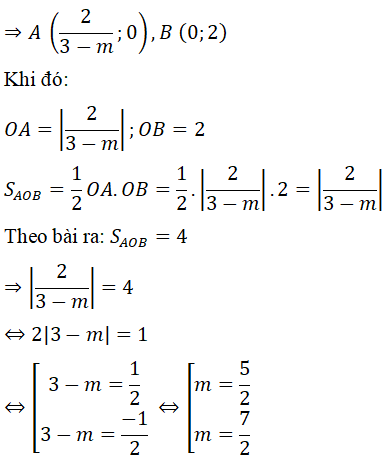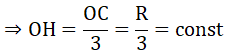Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án (Đề 4)
-
3102 lượt thi
-
18 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 6:
Cho tam giác BDC vuông tại D, ∠B = 600 , BD = 3 cm. Độ dài cạnh DC bằng:
Đáp án là B
Câu 8:
Cho đoạn thẳng OI = 8 cm. Vẽ các đường tròn (O; 10cm); (I; 2cm). Hai đường tròn (O) và (I) có vị trí tương đối như thế nào với nhau?
Đáp án là A
Câu 9:
Phần tự luận
Nội dung câu hỏi 1
Cho biểu thức
P=(3√x√x+2+√x2√x+8√xx-4)÷(2-2√x+3√x+2)
a) Rút gọn P
với x≥0;x≠4
Câu 11:
Cho biểu thức
P=(3√x√x+2+√x2-√x+8√xx-4):(2-2√x+3√x+2)
c) Tìm m để có một giá trị x thỏa mãn :
P(√x - 2) + √x (m - 2x) - √x = m - 1
Để tồn tại 1 giá trị của x thỏa mãn đề bài thì: m = 2x + 1 phải thỏa mãn với x = 1
Thay x = 1 vào ta được: m = 2.1 + 1 = 3
Vậy m = 3 thỏa mãn đầu bài.
Câu 12:
Cho hàm số y =(m – 3)x + 2 có đồ thị là (d)
a) Tìm m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng – 3. Khi đó (d) tạo với trục Ox một góc nhọn hay góc tù. Vì sao?
Cho hàm số y = (m – 3)x + 2 có đồ thị là (d)
a) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng – 3 khi:
0 = (m - 3).(-3) + 2 ⇔ 3m = 11 ⇔ m = 11/3
Khi đó (d) có phương trình là:
y = (11/3 - 3)x + 2 = 2/3 x + 2
Có hệ số a = 2/3 > 0
⇒ (d) tạo với trục Ox một góc nhọn
Câu 13:
Cho hàm số y =(m – 3)x + 2 có đồ thị là (d)
b) Vẽ đồ thị với m tìm được ở câu a.
b) Tập xác định của hàm số R
Bảng giá trị
| x | 0 | - 3 |
| y = 2/3 x + 2 | 2 | 0 |
Câu 14:
Cho hàm số y =(m – 3)x + 2 có đồ thị là (d)
c) Tìm m để (d) cắt hai trục tọa độ tạo thành một tam giác có diện tích bằng 4.
c) y = (m – 3)x + 2 (m ≠ 3)
Gọi A, B lần lượt là giao điểm của (d) và trục Ox, Oy và tam giác tạo thành là tam giác AOB vuông tại O
Câu 15:
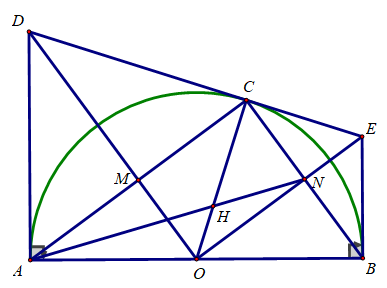
Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E.
a) Chứng minh rằng AD + BE = DE
a) CE và EB là 2 tiếp tuyến cắt nhau tại E
⇒ EC = EB và CB ⊥ OE
Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DA và AC ⊥ OD
Khi đó: AD + BE = DC + EC = DE
Câu 16:
Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E.
b) AC cắt DO tại M, BC cắt OE tại N. Tứ giác CMON là hình gì? Vì sao?
b) Xét tứ giác OMCN có:
∠(OMC) =900 (AC ⊥ OD)
∠(ONC) =900 (CB ⊥ OE)
∠(NCM) = 900 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật
Câu 17:
Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E.
c) Chứng minh rằng OM.OD + ON.OE không đổi
c) Xét tam giác DOC vuông tại C, CM là đường cao có:
OM.OD = OC2=R2
Xét tam giác EOC vuông tại C, CN là đường cao có:
ON.OE = OC2=R2
Khi đó: OM.OD + ON.OE = 2R2
Vậy OM.OD + ON.OE không đổi
Câu 18:
Cho nửa đường tròn (O; R) đường kính AB cố định. Trên cùng một nửa mặt phẳng bờ AB chứa đường tròn, vẽ các tiếp tuyến Ax, By với nửa đường tròn. Trên nửa đường tròn, lấy điểm C bất kì. Vẽ tiếp tuyến (O) tại C cắt Ax, By lần lượt tại D và E.
d) AN cắt CO tại điểm H. Điểm H di chuyển trên đường nào khi C di chuyển trên nửa đường tròn (O; R).
d) Ta có: N là trung điểm của BC
⇒ AN là trung tuyến của ΔABC
CO cũng là trung tuyến của ΔABC
AN ∩ CO = H
⇒ H là trọng tâm ΔABC
Vậy khi C di chuyển trên nửa đường tròn (O) thì H di chuyển trên nửa đường tròn
(O; R/3)