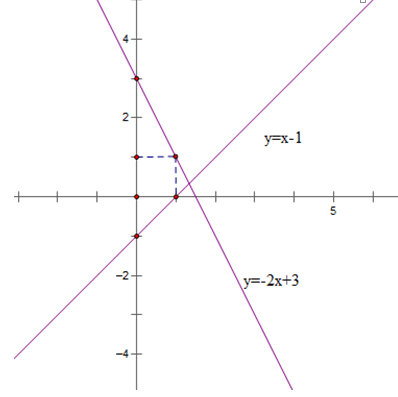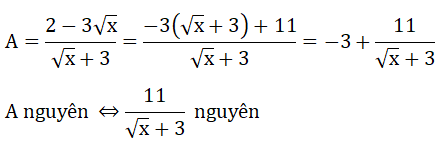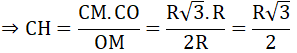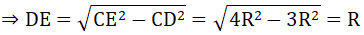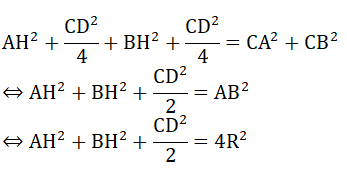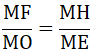13 câu hỏi trắc nghiệm thuộc Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án (Đề 2)

Câu 1:

Thực hiện các phép tính:

a) ( $\sqrt{75}$ - 3 $\sqrt{2}$ - $\sqrt{12}$ )( $\sqrt{3}$ + $\sqrt{2}$ )

Xem đáp án

a) ( $\sqrt{75}$ - 3 $\sqrt{2}$ - $\sqrt{12}$ )( $\sqrt{3}$ + $\sqrt{2}$ )

=(5 $\sqrt{3}$ - 3 $\sqrt{2}$ - 2 $\sqrt{3}$ )( $\sqrt{3}$ + $\sqrt{2}$ )

=3( $\sqrt{3}$ - $\sqrt{2}$ )( $\sqrt{3}$ + $\sqrt{2}$ ) = 3

Câu 2:

Thực hiện các phép tính:

b)

(\frac{5 - \sqrt{5}}{5} - 2) (\frac{4}{1 + \sqrt{5}} + 4)

Xem đáp án

Câu 3:

Thực hiện các phép tính:

c)

(\sqrt{5} - 2) \sqrt{3 + \sqrt{5}} + (\sqrt{5} + 2) \sqrt{3 - \sqrt{5}}

Xem đáp án

Câu 4:

Giải phương trình

a) $\sqrt{{(2 x - 1)}^{2}} = x + 2$

Xem đáp án

Câu 5:

Giải phương trình

b) $\sqrt{4 x - 12} + \frac{1}{3} \sqrt{9 x - 27} - 2 \sqrt{\frac{x - 3}{4}} = 4$

Xem đáp án

⇔ x - 3 = 4

⇔ x = 7 (TM ĐKXĐ)

Vậy phương trình có nghiệm x = 7

Câu 6:

Cho hàm số y = –2x + 3 có đồ thị ( $d_{1}$ ) và hàm số y = x – 1 có đồ thị ( $d_{2}$ )

a) Vẽ ( $d_{1}$ ) và ( $d_{2}$ ) trên cùng một mặt phẳng tọa độ.

Xem đáp án

a) Tập xác định của hàm số R

Bảng giá trị

x	0	1
y = -2x + 3	3	1

x	0	1
y = x – 1	- 1	0

Câu 7:

Cho hàm số y = –2x + 3 có đồ thị (d1) và hàm số y = x – 1 có đồ thị ( $d_{2}$ )

b) Xác định hệ số a và b biết đường thẳng ( $d_{3}$ ): y = ax + b song song với ( $d_{2}$ ) và cắt ( $d_{1}$ ) tại điểm nằm trên trục tung.

Xem đáp án

b) Do ( $d_{3}$ ) song song với đường thẳng ( $d_{2}$ ) nên ( $d_{3}$ ) có dạng: y = x + b (b ≠ -1)

( $d_{1}$ ) cắt trục tung tại điểm (0; 3)

Do ( $d_{3}$ ) cắt ( $d_{1}$ ) tại điểm nằm trên trục tung nên ta có:

3 = 0 + b ⇔ b = 3

Vậy phương trình đường thẳng ( $d_{3}$ ) là y = x + 3

Câu 8:

Cho biểu thức :

$A = \frac{15 \sqrt{x} - 11}{x + 2 \sqrt{x} - 3} + \frac{3 \sqrt{x} - 2}{1 - \sqrt{x}} - \frac{3}{\sqrt{x} + 3}$ $(x \geq 0; x \neq 1)$

a) Thu gọn biểu thức A.

Xem đáp án

x + 2 $\sqrt{x}$ - 3 = x - $\sqrt{x}$ + 3 $\sqrt{x}$ - 3 = $\sqrt{x}$ ( $\sqrt{x}$ - 1) + 3( $\sqrt{x}$ - 1) = ( $\sqrt{x}$ - 1)( $\sqrt{x}$ + 3)

a) Với điểu kiện x ≥ 0; x ≠ 1 ta có:

Câu 9:

Cho biểu thức :

$A = \frac{15 \sqrt{x} - 11}{x + 2 \sqrt{x} - 3} + \frac{3 \sqrt{x} - 2}{1 - \sqrt{x}} - \frac{3}{\sqrt{x} + 3}$ $(x \geq 0; x \neq 1)$

b) Tìm x nguyên để A nguyên.

Xem đáp án

b) Tìm x nguyên để A nguyên

⇔ $\sqrt{x}$ + 3 ∈ Ư(11) ⇔ $\sqrt{x}$ + 3 ∈ {-11; -1; 1; 11}

Do $\sqrt{x}$ + 3 ≥ 3 nên $\sqrt{x}$ + 3 = 11 ⇔ $\sqrt{x}$ = 8 ⇔ x = 64

Vậy với x = 64 thì A nguyên

Câu 10:

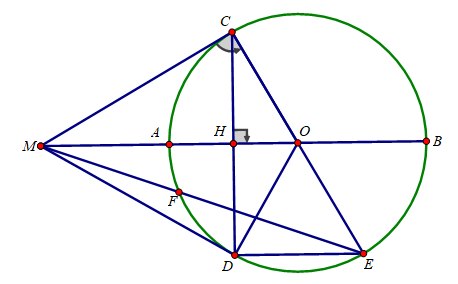
Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.

a) Chứng minh MD là tiếp tuyến của đường tròn (O).

Xem đáp án

a) Xét tam giác COD cân tại O có OH là đường cao

⇒ OH cũng là tia phân giác ⇒ ∠(COM) = ∠(MOD)

Xét ΔMCO và ΔMOD có:

CO = OD

∠(COM) = ∠(MOD)

MO là cạnh chung

⇒ ΔMCO = ΔMOD (c.g.c)

⇒ ∠(MCO) = ∠(MDO)

∠(MCO) = $90^{0}$ nên ∠(MDO) = $90^{0}$

⇒ MD là tiếp tuyến của (O)

Câu 11:

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.

b) Kẻ đường kính CE của đường tròn (O). Tính MC, DE theo R.

Xem đáp án

b) Ta có: OM = OA + AM = R + R = 2R

Xét tam giác MCO vuông tại C, CH là đường cao có:

${MO}^{2} = {MC}^{2} + {OC}^{2}$

CH.OM = CM.CO

Lại có: CD = 2CH ⇒ CD = R $\sqrt{3}$

Tam giác CDE nội tiếp (O) có CE là đường kính nên ΔCDE vuông tại D

Theo định lí Py ta go ta có:

${CE}^{2} = {CD}^{2} + {DE}^{2}$

Câu 12:

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.

c) Chứng minh $H A^{2} + H B^{2} + C D^{2} / 2 = 4 R^{2}$

Xem đáp án

c) Ta có: ΔCOD cân tại O có OH là đường cao cũng là đường trung tuyến của tam giác

⇒ CH = HD = CD/2 ⇒ $C H^{2} = D H^{2} = C D^{2} / 4$

Tam giác ACH vuông tại H có:

$A H^{2} + C H^{2} = C A^{2} \Rightarrow A H^{2} + C D^{2} / 4 = C A^{2}$ (1)

Tam giác CHB vuông tại H có:

$B H^{2} + C H^{2} = C B^{2} \Rightarrow B H^{2} + C D^{2} / 4 = C B^{2}$ (2)

Từ (1) và (2) ta có:

Câu 13:

Cho đường tròn (O;R) đường kính AB. Trên tia đối của tia AB lấy điểm M sao cho MA = R. Vẽ tiếp tuyến MC với đường tròn (O) (C là tiếp điểm ). Vẽ dây CD vuông góc với AB tại H.

d) ME cắt đường tròn (O) tại F (khác E). Chứng minh: ∠(MOF) = ∠(MEH )

Xem đáp án

d) Ta có: ∠(CFE) = $90^{0}$ (F thuộc đường tròn đường kính CE)

Lại có CF là đường cao nên ${MC}^{2}$ = MF.ME

Tương tự, ta có: ${MC}^{2}$ = MH.MO

⇒ ME.MF = MH.MO

⇒

Xét ΔMOF và ΔMEN có:

∠(FMO) chung

⇒ ΔMOF ∼ ΔMEN (c.g.c)

⇒ ∠(MOF) = ∠(MEH)

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án

Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án (Đề 2)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương