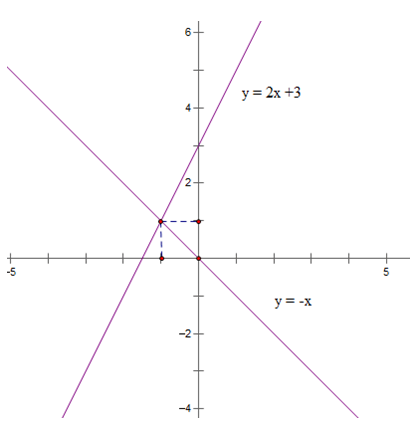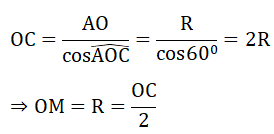Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án (Đề 3)
-
3099 lượt thi
-
13 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 4:
Cho hàm số y = 2x + 3 có đồ thị () và hàm số y = – x có đồ thị ().
a) Vẽ () và () trên cùng một mặt phẳng tọa độ.
a) Tập xác định R
Bảng giá trị:
| x | 0 | -1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | -1 |
| y = - x | 0 | 1 |
Câu 5:
Cho hàm số y = 2x + 3 có đồ thị () và hàm số y = – x có đồ thị ().
b) Tìm tọa độ giao điểm của () và () bằng phép toán.
Gọi ( ) là tọa độ giao điểm của và
Khi đó ta có:
( = 2 + 3 và = -
⇒ - = 2 + 3 ⇔ 3 = -3 ⇔ = -1
⇒ = - = 1
Vậy tọa độ giao điểm của và là (- 1; 1)
Câu 7:
Cho biểu thức:
b) Tìm giá trị nhỏ nhất của A.
Vậy GTNN của biểu thức A là 0, đạt được khi x = 0
Câu 10:
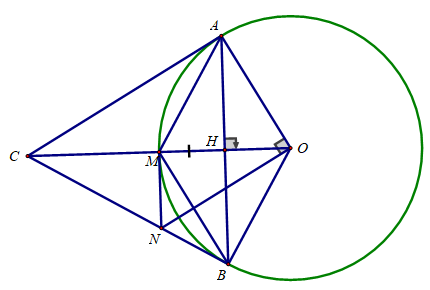
Cho đường tròn (O;R) và điểm M thuộc đường tròn (O). Đường trung trực của đoạn thẳng OM cắt đường tròn (O) tại A và B và cắt OM tại H.
a) Chứng minh H là trung điểm của AB và tam giác OMA đều.
a) Chứng minh H là trung điểm của AB
Ta có OM vuông góc AB tại H (gt)
Vậy H là trung điểm của AB (đường kính vuông góc với một dây cung)
Chứng minh tam giác OAM đều:
Ta có: AM = AO (A là trung trực của OM)
và OA = OM = R
Suy ra AM = AO = OM
Vậy ΔOAM đều.
Câu 11:
Cho đường tròn (O;R) và điểm M thuộc đường tròn (O). Đường trung trực của đoạn thẳng OM cắt đường tròn (O) tại A và B và cắt OM tại H.
b) Chứng minh tứ giác OAMB là hình thoi.
b) Chứng minh tứ giác OAMB là hình thoi.
Do H là trung điểm của AB (cmt)
H là trung điểm của OM
nên tứ giác OAMB là hình bình hành mà OM vuông góc AB.
Vậy tứ giác OAMB là hình thoi.
Câu 12:
Cho đường tròn (O;R) và điểm M thuộc đường tròn (O). Đường trung trực của đoạn thẳng OM cắt đường tròn (O) tại A và B và cắt OM tại H.
c) Tiếp tuyến tại A của (O) cắt tia OM tại C. Chứng minh CB = CA.
c) Xét ΔOAC và ΔOBC có:
OA = OB = R
∠(AOC) = ∠(BOC) (tính chất đường chéo hình thoi)
OC là cạnh chung
⇒ ΔOAC = ΔOBC (c.g.c)
⇒ AC = BC
Câu 13:
Cho đường tròn (O;R) và điểm M thuộc đường tròn (O). Đường trung trực của đoạn thẳng OM cắt đường tròn (O) tại A và B và cắt OM tại H.
d) Đường thẳng vuông góc với OA tại O cắt BC tại N. Chứng minh MN là tiếp tuyến của đường tròn (O).
d) Ta có: CA ⊥ OA (CA là tiếp tuyến của (O)
và ON ⊥ OA (gt)
⇒ CA // ON ⇒ ∠(CON) = ∠(ACO) (sole trong)
Mà ∠(ACO) = ∠(BCO) (ΔOAC = ΔOBC)
⇒ ∠(CON) = ∠(BCO) ⇒ ΔNCO cân tại N
Xét tam giác CAO vuông tại A có ∠(AOC) = 60o( ΔAMO đều) nên:
⇒ M là trung điểm của OC
ΔNCO cân tại N có NM là trung tuyến ⇒ NM cũng là đường cao
Hay NM là tiếp tuyến của (O)