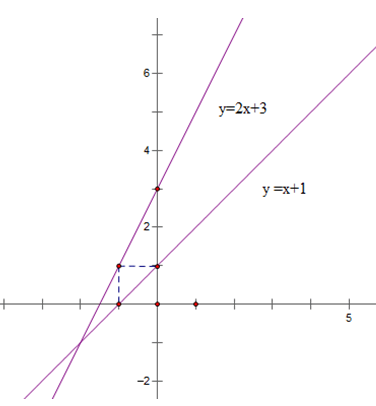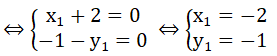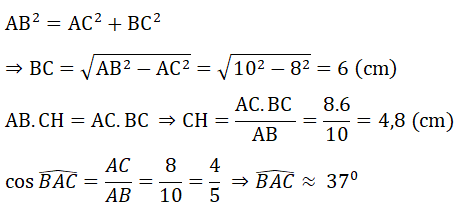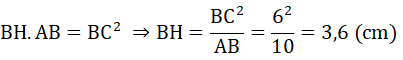Đề thi Học kì 1 Toán 9 chọn lọc, có đáp án (Đề 5)
-
3096 lượt thi
-
18 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 7:
Cho (O; 6cm) và đường thẳng a. Gọi d là khoảng cách từ tâm O đến a. Điều kiện để a cắt (O) là:
Đáp án là D
Câu 9:
Phần tự luận
Nội dung câu hỏi 1
Cho biểu thức:
với x > 0, x khác 4
a) Rút gọn biểu thức P
a) Với x > 0; x ≠ 4,ta có:
Câu 12:
Cho đường thẳng :y = mx + 2m - 1 (với m là tham số) và : y = x + 1
a) Với m = 2. Hãy vẽ các đường thẳng và trên cùng một mặt phẳng tọa độ. Tìm tọa độ gia điểm của hai đường thẳng và
Với m = 2 thì : y = 2x + 3; : y = x + 1
Tập xác định của hàm số R
Bảng giá trị
| x | 0 | - 1 |
| y = 2x + 3 | 3 | 1 |
| x | 0 | - 1 |
| y = x + 1 | 1 | 0 |
Gọi A (; ) là tọa độ giao điểm của d1 và d2
Khi đó:
( = 2 + 3 và = + 1
⇒ 2xo + 3 = + 1 ⇔ = -2
⇒ = + 1 = -2 + 1 = -1
Vậy tọa độ giao điểm của và là (-2; -1)
Câu 13:
Cho đường thẳng :y = mx + 2m - 1 (với m là tham số) và : y = x + 1
b) Tìm giá trị của m để đường thẳng cắt trục hoành tại điểm có hoành độ bằng – 3.
b) cắt trục hoành tại điểm có hoành độ bằng – 3 khi:
0 = -3m + 2m - 1 ⇔ -m - 1 = 0 ⇔ m = -1
Vậy với m = -1 thì cắt trục hoành tại điểm có hoành độ bằng – 3
Câu 14:
Cho đường thẳng :y = mx + 2m - 1 (với m là tham số) và : y = x + 1
c) Chứng mình rằng đường thẳng luôn đi qua một điểm cố định với mọi giá trị của m.
c) Giả sử đường thẳng luôn đi qua một điểm cố định (; ) với mọi giá trị của m.
⇒ = m + 2m - 1 với mọi m
⇔ m( + 2) - 1 - = 0 với mọi m
Vậy điểm cố định mà luôn đi qua với mọi giá trị của m là (-2; -1).
Câu 15:
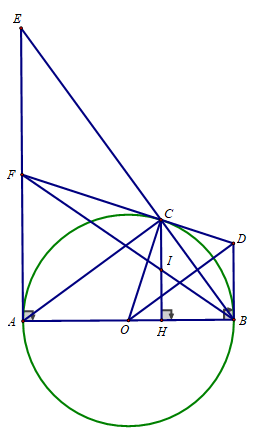
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
a) Chứng minh tam giác ABC vuông. Tính độ dài CH và số đo ∠(BAC) (làm tròn đến độ)
a) Tam giác ABC nội tiếp (O) có AB là đường kính
⇒ ∠(ACB) = 90o
Hay tam giác ABC vuông tại C
Tam giác ABC vuông tại C, CH là đường cao có:
Câu 16:
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
b) Tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại D. Chứng minh OD ⊥ BC
b) DC và DB là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DB
Lại có: OC = OB = R
⇒ OD là đường trung trực của BC hay OD ⊥ BC
Câu 17:
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
c) Tiếp tuyến tại A của đường tròn (O) cắt BC tại E. Chứng minh:CE.CB = AH. AB
c) Xét tam giác ACB vuông tại C, CH là đường cao nên :
AH.AB =
Xét tam giác ABE vuông tại A, AC là đường cao nên :
EC.BC =
⇒ AH.AB = EC.BC
Câu 18:
Cho đường tròn (O) đường kính AB = 10 cm C là điểm trên đường tròn (O) sao cho AC = 8 cm. Vẽ CH ⊥ AB (H ∈ AB)
d) Gọi I là trung điểm của CH. Tia BI cắt AE tại F. Chứng minh: FC là tiếp tuyến của đường tròn (O).
d) Xét tam giác ACB vuông tại C, CH là đường cao nên :
Xét tam giác ABE vuông tại A, AC là đường cao nên :
⇒ EA = 2 FA ⇒ F là trung điểm của EA
Tam giác CEA vuông tại C có CF là trung tuyến
⇒ FC = FA
⇒ ΔFCA cân tại F ⇒ ∠(FCA) = ∠(FAC)
Lại có ΔOCA cân tại O ⇒ ∠(OCA) = ∠(OAC)
⇒ ∠(FCA) + ∠(OCA) = ∠(FAC) + ∠(OAC)
⇔ ∠(FCO) = ∠(FAO) =
Vậy FC ⊥ CO hay FC là tiếp tuyến của (O)