Chủ đề 10: Phương trình, bất phương trình bậc hai trong các bài toán thực tiễn
-
2154 lượt thi
-
6 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Sau khi gặp nhau tại một điểm A trên mặt biển, một tàu đi về phía Nam, một tàu đi về phía Đông với vận tốc lớn hơn vận tốc tàu kia 6km/h. Hai giờ sau khi gặp nhau, hai tàu cách nhau 60km. Tính vận tốc của mỗi tàu.
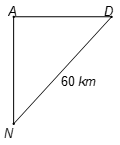
Gọi x (km/h) là vận tốc của tàu đi về phía Nam, x > 0.
Suy ra x + 6 (km/h) là vận tốc của tàu đi về phía Đông.
Sau 2 giờ, khoảng cách từ A đến tàu đi về phía Nam là: (km) và khoảng cách từ A đến tàu đi về phía Đông là: (km).
Tam giác ADN vuông góc tại A nên khoảng cách DN của hai tàu cho bởi:
.
Hay ta có
.
Ta được phương trình bậc hai:
Giải phương trình ta được (loại).
Vậy vận tốc tàu đi về phía Nam là 18km/h.
Vận tốc tàu đi về phía Đông là 24km/h.
Câu 2:
Hai địa điểm A, B cách nhau 120km trên một đường thẳng. Một xe mô tô khởi hành từ A chạy về B với vận tốc 80km/h. Cùng lúc đó, một xe đạp khởi hành từ B chạy trên đường thẳng vuông góc với AB với vận tốc 10km/h. Hỏi sau bao lâu khoảng cách giữa 2 xe là ngắn nhất.
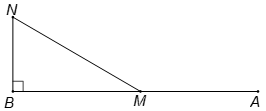
Gọi M là vị trí xe mô tô sau khi khởi hành t (h) và
N là vị trí xe đạp sau khi khởi hành t (h).
Ta có: .
.
Sử dụng định lí Pythagore, ta được:
.
Vậy MN ngắn nhất khi 3,6 (h) 3 giờ 36 phút.
Câu 3:
Một ô tô C, một xe đạp B và điểm cố định A đang ở vị trí tạo thành tam giác vuông tại B. Ô tô và xe đạp khởi hành cùng một lúc đi về phía A theo các cạnh của tam giác ABC. Sau khi ô tô đi được 25km thì tam giác tạo bởi điểm A, ô tô C, xe đạp B là tam giác đều. Khi ô tô đến A thì xe đạp còn phải đi 12km nữa mới đến A. Tìm khoảng cách ban đầu của ô tô và xe đạp.
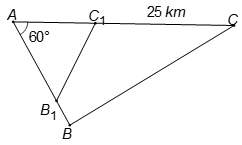
Góc A của tam giác vuông ABC với góc A là góc của tam giác đều là một góc.
Vậy .
Giả sử lúc đầu (km). Vậy (km).
Ta có: .
Gọi là vận tốc ô tô; là vận tốc xe đạp. Ta có:
Hệ phương trình này đưa đến phương trình
, .
Giải phương trình ta được x = 40.
Vì (km).
Câu 4:
Người ta phải đắp 100m nền của đường ray xe lửa có thiết diện ngang là một hình thang cân, đáy dưới dài 5m, đáy trên không nhỏ hơn 3m, độ dốc hai bên bằng 450. Tính chiều cao của nền sao cho thể tích đào đắp không nhỏ hơn và không lớn hơn đất.
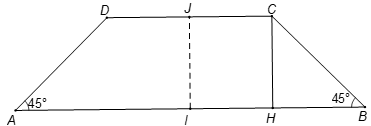
Gọi độ dài của đáy nhỏ của nền là:
I là trung điểm của AB, J là trung điểm của CD.
Kẻ CH vuông góc với AB tại H.
Ta có: .
Tam giác CHB vuông cân nên:
.
Diện tích hình thang cân ABCD là:
Thể tích đất đào để đắp là: .
Theo giả thiết, ta có:
x thoả hệ bất phương trình:
Đường cao
Vậy .
Vậy chiều cao của nên phải thoả mãn .
Câu 5:
Hai chiếc thuyền rời điểm A trên bãi biển cùng một lúc và đi theo hai hướng vuông góc với nhau. Nửa giờ sau, hai thuyền cách nhau 15km. 15 phút theo đó thuyền thứ nhất cách xa A hơn thuyền thứ hai 4,5km. Hỏi vận tốc của mỗi thuyền.
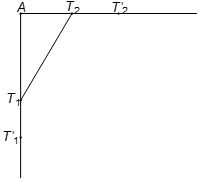
Gọi (km/h) là vận tốc của thuyền 1,
(km/h) là vận tốc của thuyền 2.
và là vị trí của thuyền 1, 2 sau 30 phút.
và là vị trí của thuyền 1, 2 sau 15 phút nữa.
Theo giả thiết: .
Đưa đến hệ: dẫn đến .
Giải phương trình ta được (km/h) thoả mãn bài toán
Vậy vận tốc thuyền 1 là 24 (km/h) và vận tốc thuyền 2 là 18 (km/h).
Câu 6:
Cho tam giác ABC vuông góc tại A, đường cao AH. Độ dài AB=12cm, độ dài HC=12,8cm. Tính các cạnh của tam giác ABC.
Đặt (m); x > 0.
x là nghiệm của hệ phương trình: .
Giải phương trình ta được x=7,2.
Đáp số: (m); (m).
