Chủ đề 3: Định lí THALES trong các bài toán thực tế có đáp án
-
2160 lượt thi
-
6 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
Làm thế nào đo được độ cao của kim tự tháp?
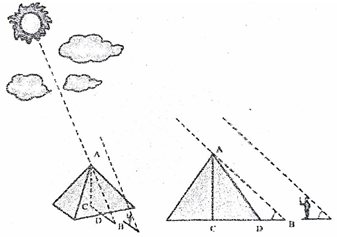
Kim tự tháp là công trình kiến trúc cổ rất hùng vĩ và là phần mộ của các vua chúa Ai Cập cổ đại. Hơn 2600 năm trước, có một vương quốc Ai Cập muốn biết độ cao thực sự của kim tự tháp là bao nhiêu, nhưng chẳng ai đo được.
Cho người trèo lên đỉnh tháp? Rõ ràng là không thể được vì tháp nghiêng, có trèo lên được cũng chẳng biết dùng cách gì để đo được.
Thales được cho là người đã giúp Quốc Vương đo được chiều cao của kim tự tháp. Thales chọn một ngày đẹp trời, mời Quốc Vương và các quan trọng triều của hành lễ đo tháp. Người đến xem rất đông, chen chúc nhau, bàn ra tán vào rất sôi nổi. Nhưng thời gian cứ trôi đi, mặt trời cứ chiếu xuống Kim tự tháp và đám người mà chưa thấy Thales có động tĩnh gì. Mãi khi thấy bóng người bằng chính chiều cao của ông, ông mới phát lệnh đo tháp. Lúc đó, người giúp việc lập tức đo độ dài của bóng Kim tự tháp bằng DB (hình vẽ trên). Sau đó, ông đưa ra ngay chiều cao của Kim tự tháp một cách hết sức chuẩn xác.
Thales làm thế nào để đo được chiều cao của Kim tự tháp? Ông phải chờ tới khi độ dài của bóng người ông bằng chính độ cao của ông mới đo, chính lúc đó tia nắng mặt trời và người ông tạo thành một góc 450. Tức là . Lúc ấy, điểm đỉnh của Kim tự tháp cùng với điểm trung tâm của Kim tự tháp và điểm cuối của bóng Kim tự tháp tạo thành một tam giác vuông cân, và như vậy đương nhiên hai cạnh bên . Nửa độ dài của Kim tự tháp chính là đoạn CD (đã được ông đo trước, còn độ dài đoạn bóng Kim tự tháp chính DB ông nhờ các trợ lý đo. Cuối cùng chỉ việc cộng lại hai đoạn CD và DB lại là ra chiều cao Kim tự tháp.
Câu 2:
Làm thế nào để đo được chiều cao của cây?
Cách 1 (Phương pháp dùng gậy – nằm trên mặt đất)
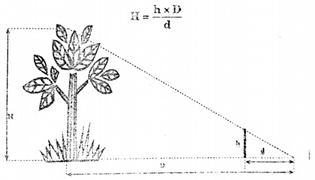
Phương pháp đo cây sau đòi hỏi phải có một khoảng đất trống vừa đủ rộng. Các bước thực hiện như sau:
- Gọi chiều cao của cây là ![]() .
.
- Cắm 1 cây sậy có chiều cao là h cách gốc cây một khoảng sao cho có thể lấy số đo.
- Nằm xuống và ngắm sao cho ngọn cây trùng với đỉnh của gậy. Bây giờ mắt người, đỉnh gậy và ngọn cây thẳng hàng.
- Gọi đoạn từ vị trí đặt mắt đến gốc cây là D, từ mắt đến nơi cắm gậy là d. Theo định lí Thales, ta có: .
Vậy chiều cao của cây là: .
Cách 2 (Phương pháp dùng gậy và bóng nắng)
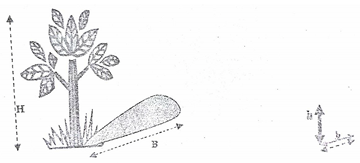
Nếu có ánh mặt trời, ta đo chiều cao bằng cách cắm một gậy xuống đất, đo chiều dài của bóng cây và bóng gậy in trên mặt đất. Gọi:
- H là chiều cao của cây muốn đo.
- B là chiều dài của bóng cây.
- h là chiều cao cây gậy.
- b là chiều dài của bóng cây.
Theo định lí Thales, ta có: .
Cách 3 (Phương pháp “Cách ngắm của Hoạ sĩ”)
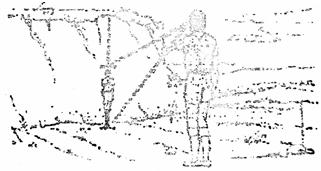
- Đặt dưới chân mục tiêu (ở đây là cây) cần đo một cây gậy chuẩn (hay một người đứng ngay chỗ mục tiêu) mà ta đã biết rõ chiều cao.
- Đứng cách xa mục tiêu một khoảng cách gấp 2-3 lần chiều cao phỏng đoán của mục tiêu.
- Cầm một cây que hoặc một cây bút dang thẳng tay ra đằng trước.
- Bấm ngón tay trên que để ghi dấu chỗ trên mặt đất.
- Sau đó, chúng ta đo ướm dần lên xem mục tiêu cao hơn vật chuẩn mấy lần.
- Nhân chiều cao của vật chuẩn với số lần đó thì ta có chiều cao mục tiêu.
Nhận xét
Ta hoàn toàn áp dụng được các phương pháp đo chiều cao của cây đối với chiều cao của Kim tự tháp.
Câu 3:
Làm thế nào để đo được chiều rộng của một con sông?
Cách 1 (Phương pháp hai tam giác vuông bằng nhau)
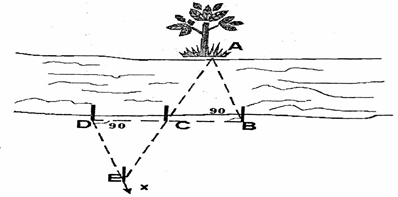
- Ta chọn một điểm gốc A bên kia mép bờ sông, đối diện bờ sông bên này ta đóng một cọc B sát bờ.
Từ B ta xoay một góc 900 rồi đo 1 điểm bất kỳ để đóng cọc C, kéo dài BC chọn điểm D sao cho CB=CD.
- Tại D kẻ một tia Dx vuông góc với BD (góc vuông tại D)
- Trên tia Dx xác định điểm E sao cho A, C, E thẳng hàng.
- Ta có hai tam giác vuông . Vậy .
- Đo ED chính là khoảng cách AB (chiều rộng bờ sông) cần tìm.
Cách 2 (Phương pháp tam giác đồng dạng)
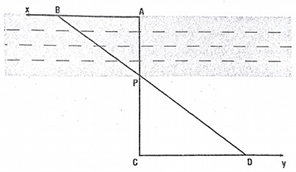
- Chọn một điểm P sát bên kia bờ sông, đối diện sát bờ sông bên này đóng một cọc A. Từ PA ta nối dài đóng một cọc tiêu C.
- Kẻ tia Ax vuông góc với PC tại A, trên tia Ax đóng cọc tiêu B.
- Kẻ tia Cy vuông góc với PC tại C, trên tia Cy xác định cọc tiêu D sao cho P, B, D thẳng hàng. (Xem hình vẽ).
- Hai tam giác PAB và PCD đồng dạng. Nên theo định lí Thales ta có:
.
Câu 4:
Cho tam giác ABC. Gọi G là trọng tâm của tam giác ABC. Qua G vẽ GD song song với AB .
a) Tính tỉ số ?
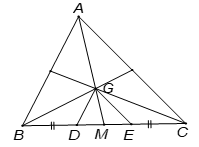
Theo định lí Thales, ta có:
Vậy: