11 câu hỏi trắc nghiệm thuộc Chủ đề 15: Hình cầu, diện tích mặt cầu và thể tích hình cầu

Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 9: Bài toán thực tế Hình học có đáp án

Chủ đề 15: Hình cầu, diện tích mặt cầu và thể tích hình cầu

1860 lượt thi
11 câu hỏi
60 phút

Danh sách câu hỏi

Câu 1:

Ngày 4-6-1983, anh em nhà Montgolfier (người Pháp) phát minh ra khinh khí cầu dùng khinh khí nóng. Coi khinh khí cầu này là hình cầu có đường kính 11m. Hãy tính diện tích mặt khinh khí cầu đó (làm tròn kết quả đến chữ số thập phân thứ hai).

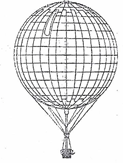
Ngày 4-6-1983, anh em nhà Montgolfier (người Pháp) phát minh ra khinh khí cầu dùng khinh (ảnh 1)

Xem đáp án

Sử dụng công thức tính diện tích mặt cầu:

$S = 4 π R^{2} \approx {4.3,14.5,5}^{2} \approx 380 (m^{2})$

Câu 2:

Cần phải có ít nhất bao nhiêu lít nước để thay nước ở liễn nuôi cá cảnh (hình vẽ)? Liễn được xem như một phần mặt cầu (đường kính của mặt cầu là 22cm). Lượng nước đổ vào liễn chiến $\frac{2}{3}$ thể tích hình cầu.

Cần phải có ít nhất bao nhiêu lít nước để thay nước ở liễn nuôi cá cảnh (hình vẽ)? Liễn được xem (ảnh 1)

Xem đáp án

Thể tích hình cầu được tính theo công thức:

$V = \frac{4}{3} π R^{3}$ hay $V = \frac{1}{3} π d^{3}$ (d là đường kính).

$22 c m = 2,2 d m$ .

Lượng nước ít nhất cần phải có là:

$\frac{2}{3} . \frac{π}{6} . {(2,2)}^{3} \approx 3,71 (d m^{3}) = 3,71$ lít.

Câu 3:

Một khối gỗ dạng hình trụ, bán kính đường tròn đáy là r, chiều cao 2r (đơn vị: cm). Người ta khoét rỗng hai nữa hình cầu như hình vẽ.

Hãy tính diện tích bề mặt của khối gỗ còn lại (diện tích cả ngoài lẫn trong).

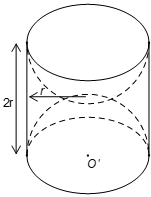
Một khối gỗ dạng hình trụ, bán kính đường tròn đáy là r, chiều cao 2r (đơn vị: cm). Người ta khoét (ảnh 1)

Xem đáp án

Diện tích bề mặt của khối gỗ còn lại gồm diện tích xung quanh của hình trụ (có bán kính đáy là r và chiều cao 2r) và diện tích hai nửa mặt cầu bán kính r.

Diện tích cần tìm là: $S = 2 π r .2 r + 4 π r^{2} = 8 π r^{2}$ .

Câu 4:

Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (hình vẽ). Hãy tính thể tích của bồn chứa theo các kích thước cho trên hình vẽ.

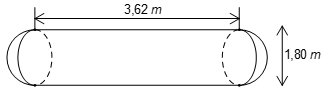
Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (hình vẽ). Hãy tính thể tích của (ảnh 1)

Xem đáp án

Thể tích của bồn chứa bằng tổng thể tích của một hình trụ (có bán kính đáy 0,9 m và chiều cao 3,62m) và thể tích của một hình cầu bán kính 0,9m.

Thể tích của bồn chứa là:

$V = π . {(0,9)}^{2} .3,62 + \frac{4}{3} π . {(0,9)}^{2} \approx 12,26 (m^{3})$

Câu 5:

Một chi tiết máy gồm một hình trụ và hai nửa hình cầu với các kích thước đã cho trên hình vẽ (đơn vị: cm).

a) Tìm một hệ thức giữa x và h khi AA' có độ dài không đổi và bằng 2a.

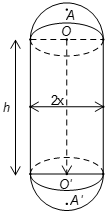
Một chi tiết máy gồm một hình trụ và hai nửa hình cầu với các kích thước đã cho trên hình vẽ (ảnh 1)

Xem đáp án

a) Ta có: $h + 2 x = A A^{'}$ . Do đó $h + 2 x = 2 a$ .

Câu 6:

b) Với điều kiện ở câu a), hãy tính diện tích bề mặt và thể tích của chi tiết máy theo x và a.

Xem đáp án

b) Diện tích bề mặt chi tiết máy là:

$S = 2 π x h + 4 π x^{2} = 2 π x (h + 2 x) = 4 π a x$

Thể tích của chi tiết máy là:

$V = π x^{2} h + \frac{4}{3} π x^{3} = 2 π x^{2} (a - x) + \frac{4}{3} π x^{3} = 2 π a x^{3} - \frac{2}{3} π x^{3}$

Câu 7:

Với hai quả dưa hấu (xem như là hai hình cầu) một to và một nhỏ, tỉ số các đường kính của chúng là 5:4, nhưng giá của quả to gấp rưỡi giá cua quả nhỏ. Bạn chọn mua quả nào thì lợi hơn? (Xem “chất lượng” của chúng là như nhau).

Xem đáp án

Mua quả to lợi hơn vì tỉ số giữa thể tích của nó với thể tích của quả nhỏ là ${(\frac{5}{4})}^{3} = \frac{125}{64}$ (gần gấp đôi).

Trong khi đó giá của nó chỉ gấp rưỡi!

(Dễ thấy $\frac{125}{64} > \frac{3}{2} = \frac{96}{64}$ ).

Câu 8:

Cho tam giác ABC cạnh a, đường cao AH. Ta quay nửa đường tròn nội tiếp và nửa đường tròn ngoại tiếp tam giác đều này một vòng quanh AH. Tính:

a) Tỉ số diện tích hai mặt cầu nội tiếp và ngoại tiếp hình nón.

Xem đáp án

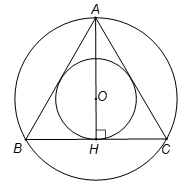
Cho tam giác ABC cạnh a, đường cao AH. Ta quay nửa đường tròn nội tiếp và nửa đường tròn (ảnh 1)

Gọi R và r lần lượt là các bán kính đường tròn ngoại tiếp và đường
tròn nội tiếp tam giác đều.

Dễ thấy R=2r.

Vì $B C = a$ nên $H C = \frac{a}{2}$ .

Và $A H = \frac{a \sqrt{3}}{2}; O A = \frac{a \sqrt{3}}{3}$ .

a) Tỉ số diện tích hai mặt cầu nội tiếp và ngoại tiếp hình nón là:

$\frac{S_{1}}{S_{2}} = \frac{4 π r^{2}}{4 π R^{2}} = \frac{r^{2}}{{(2 r)}^{2}} = \frac{1}{4}$ .

Câu 9:

b) Tỉ số thể tích của hai hình cầu nói trên.

Xem đáp án

b) Tỉ số thể tích hai hình cầu nội tiếp và ngoại tiếp hình nón là:

$\frac{V_{1}}{V_{2}} = \frac{\frac{4}{3} π r^{3}}{\frac{4}{3} π R^{3}} = \frac{r^{3}}{{(2 r)}^{3}} = \frac{1}{8}$ .

Câu 10:

c) Tính thể tích phần không gian giới hạn bởi hình nón và hình cầu ngoại tiếp hình nón.

Xem đáp án

c) Thể tích hình cầu ngoại tiếp là:

$V_{2} = \frac{4}{3} π R^{3} = \frac{4}{3} π . {(\frac{a \sqrt{3}}{3})}^{3} = \frac{4 \sqrt{3} π a^{3}}{27}$ (đvdt).

Thể tích hình nón là: $V_{3} = \frac{1}{3} π . {(\frac{a}{2})}^{2} . \frac{a \sqrt{3}}{2} = \frac{\sqrt{3} π a^{3}}{24}$ (đvdt).

Thể tích phần không gian giới hạn bởi hình nón và hình cầu ngoại tiếp là:

$V = V_{2} - V_{3} = \frac{4 \sqrt{3} π a^{3}}{27} - \frac{\sqrt{3} π a^{3}}{24} = \frac{23 \sqrt{3} π a^{3}}{216} \approx 0,58 a^{3}$ (đvdt).

Câu 11:

Một hình cầu có diện tích bề mặt là $100 π (m^{2})$ . Tính thể tích của hình cầu đó.

Xem đáp án

Theo đề bài ta có: $4 π R^{2} = 100 π \Rightarrow R = 5$ (m).

Thể tích của hình cầu đó là: $V = \frac{4}{3} π {.5}^{2} = \frac{500 π}{3} (m^{3})$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Chuyên đề Toán 9 Chuyên đề 9: Bài toán thực tế Hình học có đáp án

Chủ đề 15: Hình cầu, diện tích mặt cầu và thể tích hình cầu

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương