5 câu hỏi trắc nghiệm thuộc Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 13

Câu 1:

Cho hàm số y = 2x² có đồ thị là parabol (P).

a) Các điểm A(−2; 8); B $(\frac{1}{2}; 1)$ có thuộc (P) không? Vì sao?

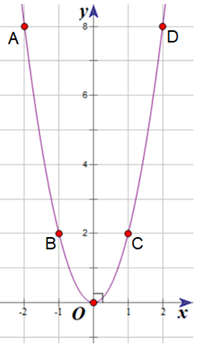
b) Vẽ parabol (P) trên mặt phẳng tọa độ Oxy.

Xem đáp án

a) Thay x_A vào hàm số y = 2x² ta có:

y = 2x_A² = 2.(−2)² = 8 = y_A.

Do đó A(−2; 8) thuộc (P).

Thay x_B vào hàm số y = 2x² ta có:

y = 2x_B² = 2. ${(\frac{1}{2})}^{2} = \frac{1}{2}$ ≠ y_B= 1.

Do đó B(; 1) không thuộc (P).

b) Bảng giá trị:

x	−2	−1	0	1	2
y = 2x²	8	2	0	2	8

Parabol (P) đi qua các điểm O(0; 0); A(−2; 8); B(−1; 2); C(1; 2); D(2; 8).

Cho hàm số y = 2x2 có đồ thị là parabol (P). (ảnh 1)

Câu 2:

a) Viết phương trình đường thẳng đi qua hai điểm M(−2; −5) và N(4; 7)

b) Giải hệ phương trình: $\{\begin{cases} (x + 1) (y - 1) = x y - 1 \\ (x - 3) (y - 3) = x y - 3 \end{cases}$

Xem đáp án

a) Phương trình đường thẳng (d) có dạng y = ax + b

Do M(−2; −5) thuộc (d) nên ta có: −2a + b = −5 (1)

Do N(4; 7) thuộc (d) nên ta có: 4a + b = 7 (2)

Từ (1) và (2) ta có hệ phương trình $\{\begin{cases} - 2 a + b = - 5 \\ 4 a + b = 7 \end{cases}$

$\Leftrightarrow \{\begin{cases} b = 2 a - 5 \\ 4 a + 2 a - 5 = 7 \end{cases} \Leftrightarrow \{\begin{cases} b = 2 a - 5 \\ 6 a = 12 \end{cases} \Leftrightarrow \{\begin{cases} b = - 1 \\ a = 2 \end{cases}$

Vậy phương trình đường thằng (d) qua M và N có dạng y = 2x – 1.

b)

$\{\begin{cases} (x + 1) (y - 1) = x y - 1 \\ (x - 3) (y - 3) = x y - 3 \end{cases} \Leftrightarrow \{\begin{cases} x y - x + y - 1 = x y - 1 \\ x y - 3 x - 3 y + 9 = x y - 3 \end{cases} \Leftrightarrow \{\begin{cases} - x + y = 0 \\ - 3 x - 3 y = - 12 \end{cases} \Leftrightarrow \{\begin{cases} x - y = 0 \\ x + y = 4 \end{cases} \Leftrightarrow \{\begin{cases} x = y \\ x + x = 4 \end{cases} \Leftrightarrow \{\begin{cases} x = y \\ 2 x = 4 \end{cases} \Leftrightarrow x = y = 2$

Vậy hệ phương trình có cặp nghiệm là (2; 2).

Câu 3:

Hai người thợ cùng làm chung một công việc thì sau 6 ngày hoàn thành. Nếu người thứ nhất làm trong 2 ngày rồi dùng là và người thứ hai làm tiếp công việc đó trong 3 ngày thì hoàn thành đươc 40% công việc. Hỏi nếu làm một mình thì mỗi người hoàn thành công việc đó trong thời gian bao lâu?

Xem đáp án

Gọi x (công việc) là phần công việc người thứ nhất làm được trong 1 ngày (x > 0)

Gọi y (công việc) là phần công việc người thứ hai làm dược trong 1 ngày (y > 0)

Hai người cùng làm chung trong 6 ngày thì xong nên ta có:

6x + 6y = 1 (1)

Người thứ nhất làm trong 2 ngày và người thứ hai làm trong 2 ngày thì được 40% công việc nên:

2x + 3y = 40% = 0,4 (2)

Từ (1) và (2) ta có hệ phương trình: $\{\begin{cases} 6 x + 6 y = 1 \\ 2 x + 3 y = 0, 4 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = \frac{1}{6} - y \\ 2 (\frac{1}{6} - y) + 3 y = 0, 4 \end{cases} \Leftrightarrow \{\begin{cases} x = \frac{1}{6} - y \\ \frac{2}{6} - 2 y + 3 y = 0, 4 \end{cases}$

$\Leftrightarrow \{\begin{cases} x = \frac{1}{10} \\ y = \frac{1}{15} \end{cases}$ (thỏa)

Người thứ nhất làm 1 ngày được $\frac{1}{10}$ công việc nên người thứ nhất làm một mình mất 10 ngày thì xong.

Người thứ hai làm 1 ngày được $\frac{1}{15}$ công việc nên người thứ hai làm một mình mất 15 ngày thì xong.

Vậy người thứ nhất làm một mình mất 10 ngày thì xong, người thứ hai làm một mình mất 15 ngày thì xong.

Câu 4:

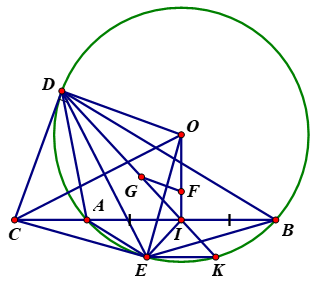
Cho đường tròn (O; R) và dây AB cố định (AB < 2R). Từ điểm C bất kì trên tia đối của tia AB, kẻ tiếp tuyến CD với đường tròn (O) (D nằm trên cung lớn AB). Gọi I là trung điểm của dây AB. Tia DI cắt đường tròn (O) tại điểm thứ hai K. Kẻ đường thẳng KE song song với AB (E ∈ (O)). Chứng minh rằng:

a) Tứ giác CDOI nội tiếp.

b) CD² = CA.CB.

c) CE là tiếp tuyến của đường tròn (O).

d) Khi C chuyển động trên tia đối của tia AB thì trọng tâm G của tam giác ABD chuyển động trên một đường tròn cố định.

Xem đáp án

Cho đường tròn (O; R) và dây AB cố định (AB < 2R). Từ điểm C bất kì trên tia đối của tia AB, kẻ tiếp tuyến CD với đường tròn (O) (D nằm (ảnh 1)

a) Ta có OI ⊥ AB (đường kính đi qua trung điểm của dây thì vuông góc với dây đó)

$\Rightarrow \hat{C I O} = 90 °$

Ta cũng có $\hat{C D O} = 90 °$ (CD là tiếp tuyến của (O))

Xét tứ giác CDOIcó $\hat{C I O} + \hat{C D O} = 90 ° + 90 ° = 180 °$

Do đó tứ giác CDOI nội tiếp.

b) Xét ∆CDA và ∆CBD có:

$\hat{D C B}$ là góc chung

$\hat{D B A} = \hat{C D A}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung DA)

Suy ra ∆CDA ∆CBD (g.g)

Từ đó suy ra $\frac{C D}{C B} = \frac{C A}{C D} \Leftrightarrow C D^{2} = C A . C B$ (điều phải chứng minh)

c) Ta có $\{\begin{cases} O I ⊥ A B (c m t) \\ A B / / E K (g t) \end{cases} \Rightarrow O I ⊥ E K$

Xét tam giác OEK có OE = OK = R => Tam giác OEK cân tại O

Tam giác OEK cân tại O có OI là đường cao (OI ⊥ EK).

Nên OI là đường trung trực của EK.

Suy ra IE = IK.

Do đó tam giác IEK cân tại I.

Ta có:

$\hat{C D E} = \hat{D K E}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung DE)

$\hat{D K E} = \hat{I E K}$ (tam giác IEK cân tại I)

$\hat{C I E} = \hat{I E K}$ (hai góc so le trong)

Suy ra $\hat{C E D} = \hat{C I D}$ suy ra tứ giác DIEC nội tiếp.

Mà tứ giác CDOI nội tiếp.

Suy ra D, O, I, E, C cùng thuộc một đường tròn.

Xét đường tròn ngoại tiếp trên ta có:

$\hat{C E O} = \hat{C I O} = 90 °$ (góc nội tiếp cùng chắn cung CO)

Suy ta CE ⊥ OE nên CE là tiếp tuyến của (O).

d) Lấy F thuộc đoạn OI sao cho IF = OI.

Ta có: A, B cố định suy ra I là trung điểm AB cố định suy ra OI cố định.

Suy ra F cố định.

Xét tam giác DAB có G là trọng tâm nên ta có: $D G = \frac{2}{3} D I$

$\Rightarrow I G = D I - D G = D I (1 - \frac{2}{3}) = \frac{1}{3} D I$

Xét tam giác IDO có: $I F = \frac{1}{3} I O; I G = \frac{1}{3} I D$ .

$\Rightarrow G F = \frac{1}{3} D O = \frac{1}{3} R$ .

Ta có F cố định và FG $= \frac{1}{3} R$ cố định.

Suy ra G thuộc

(F; \frac{1}{3} R)

cố định khi C di chuyển trên tia đối tia AB

Câu 5:

Cho a, b, c là các số thực dương thỏa mãn: ab + bc + ca = 3abc.

Tìm giá trị nhỏ nhất của biểu thức: $K = \frac{a^{2}}{c (c^{2} + a^{2})} + \frac{b^{2}}{a (a^{2} + b^{2})} + \frac{c^{2}}{b (b^{2} + c^{2})}$

Xem đáp án

Ta có: $K = \frac{a^{2}}{c (c^{2} + a^{2})} + \frac{b^{2}}{a (a^{2} + b^{2})} + \frac{c^{2}}{b (b^{2} + c^{2})} = \frac{a^{2} + c^{2} - c^{2}}{c (c^{2} + a^{2})} + \frac{b^{2} + a^{2} - a^{2}}{a (a^{2} + b^{2})} + \frac{c^{2} + b^{2} - b^{2}}{b (b^{2} + c^{2})} = (\frac{1}{c} - \frac{c}{c^{2} + a^{2}}) + (\frac{1}{a} - \frac{a}{a^{2} + b^{2}}) + (\frac{1}{b} - \frac{b}{b^{2} + c^{2}}) \geq^{C o s i} (\frac{1}{c} - \frac{c}{2 \sqrt{c^{2} a^{2}}}) + (\frac{1}{a} - \frac{a}{2 \sqrt{a^{2} b^{2}}}) + (\frac{1}{b} - \frac{b}{2 \sqrt{b^{2} c^{2}}}) = (\frac{1}{c} - \frac{1}{2 a}) + (\frac{1}{a} - \frac{1}{2 b}) + (\frac{1}{b} - \frac{1}{2 c}) = \frac{1}{2} (\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) = \frac{a b + b c + a c}{2 a b c} = \frac{3}{2} \Rightarrow K \geq \frac{3}{2}$

Vậy Min K = $\frac{3}{2}$ khi a = b = c.

Mà ab + bc + ac = 3abc

$\Rightarrow a = b = c = 1$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)

Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 13

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương