Đề kiểm tra giữa học kì 2 môn Toán 9 ( Mới nhất)_ đề 7
-
3687 lượt thi
-
4 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho các biểu thức:
và với x ≥ 0, x ≠ 4
a) Tính giá trị của biểu thức A khi x = 49.
b) Rút gọn biểu thức B.
c) Tìm x để biểu thức P = A.B ≤
a) Với x = 49 ta có:
.
b) Ta có:
.
c) P = A.B =
Ta có P ≤ Û .
Vì và x + 3 đều lớn hơn 0 ( do x ≥ 0) nên bất đẳng thức trên trở thành.
Mà dẫn đến .
Kết hợp với điều kiện đề bài thì 0 ≤ x ≤ 1 thỏa mãn biểu thức.
Câu 2:
Quãng đường AB dài 400 km, một ô tô đi từ A đến B với vận tốc không đổi. Khi từ B trở về A, ô tô tăng vận tốc thêm 10 km/h. Biết thời gian ô tô đi từ B vể A ít hơn thời gian đi từ A đến B là 2 giờ. Tính vận tốc ô tô lúc đi từ A đến B.
Gọi x (km/h) là vận tốc của ô tô khi đi từ A đến B (x > 0).
Suy ra vận tốc xe đi từ B về A là x + 10 (km/h)
Thời gian ô tô đi từ A đến B là: (h)
Thời gian ô tô đi từ B về A là: (h)
Thời gian ô tô đi từ B vể A ít hơn thời gian đi từ A đến B là 2 giờ nên ta có phương trình:
Tính ∆ = b2 – 4ac. Phương trình có các hệ số là a = 2; b = 20; c = −4 000.
∆ = 202 – 4.2.(−4 000) = 400 + 32 000 = 32 400 > 0
Do ∆ > 0, áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt:
x1 = (thỏa mãn) ; x2 = (không thỏa mãn).
Vậy vận tốc của ô tô đi từ A đến B là 40 km/h
Câu 3:
1) Giải hệ phương trình sau:
2) Cho Parabol (P): y = x2 và đường thẳng (d): y = (m + 4)x – 4m
a) Tìm m để đường thẳng (d) cắt (P) tại 2 điểm phân biệt.
b) Tìm tọa độ giao điểm của (d) và (P) khi m = −2.
1) Điều kiện xác định:
Đặt u = (u ≠ 0) và v = (v ≠ 0)
Hệ phương trình trở thành
Û Û
Û Û (thỏa mãn)
∙ u = = 1 Û 2x – 7 = 1 Û x = 4 (thỏa mãn)
∙ v = = 1 Û x + 6 = 1 Û y = −5 (thỏa mãn)
Vậy hệ phương trình có cặp nghiệm là (4; −5).
2)
a) Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = (m + 4)x – 4m
Û x2 – (m + 4)x + 4m = 0 (1)
Ta có: ∆ = [– (m + 4)]2 – 4.1.4m = m2 + 8m + 16 – 16m
= m2 – 8m + 16 = (m – 4)2.
Để đường thẳng (d) cắt (P) tại 2 điểm phân biệt thì phương trình (1) có 2 nghiệm phân biệt. Do đó ∆ = (m – 4)2 > 0 (2)
Mà (m – 4)2 ≥ 0 với mọi giá trị của m nên (2) Û (m – 4)2 ≠ 0 Û m ≠ 4.
Vậy để đường thẳng (d) cắt (P) tại 2 điểm phân biệt thì m ≠ 4.
b) Khi m = −2 ta có (d): y = (−2 + 4)x – 4.(−2) = 2x + 8
Phương trình hoành độ giao điểm của (P) và (d) là:
x2 = 2x + 8
Û x2 – 2x – 8 = 0
Û x2 + 2x – 4x – 8 = 0
Û x( x + 2) – 4(x + 2) = 0
Û (x – 4)(x + 2) = 0
Û
• Với x = 4 thì y = 2x + 8 = 2.4 + 8 = 16.
Do đó, ta có tọa độ giao điểm của (P) và (d) là A(4; 16).
• Với x = –2 thì y = 2x + 8 = 2.(–2) + 8 = 4.
Do đó, ta có tọa độ giao điểm của (P) và (d) là B(−2; 4).
Vậy hai đồ thị hàm số trên có 2 giao điểm là A(4; 16) và B(−2; 4).
Câu 4:
Cho đường tròn (O; R) và dây AB cố định không đi qua tâm. Trên tia đối của tia AB lấy điểm C (C khác A). Từ C kẻ 2 tiếp tuyến CM và CN với đường tròn (O) (M và N là các tiếp điểm; tia CO nằm giữa hai tia CM và CA). Gọi D là trung điểm AB.
a) Chứng minh tứ giác CMOD nội tiếp.
b) Chứng minh: CN2 = CA.CB
c) ND cắt (O) tại I. Chứng minh: MI // ABư
d) Gọi E là giao điểm của MN và AB. Chứng minh .
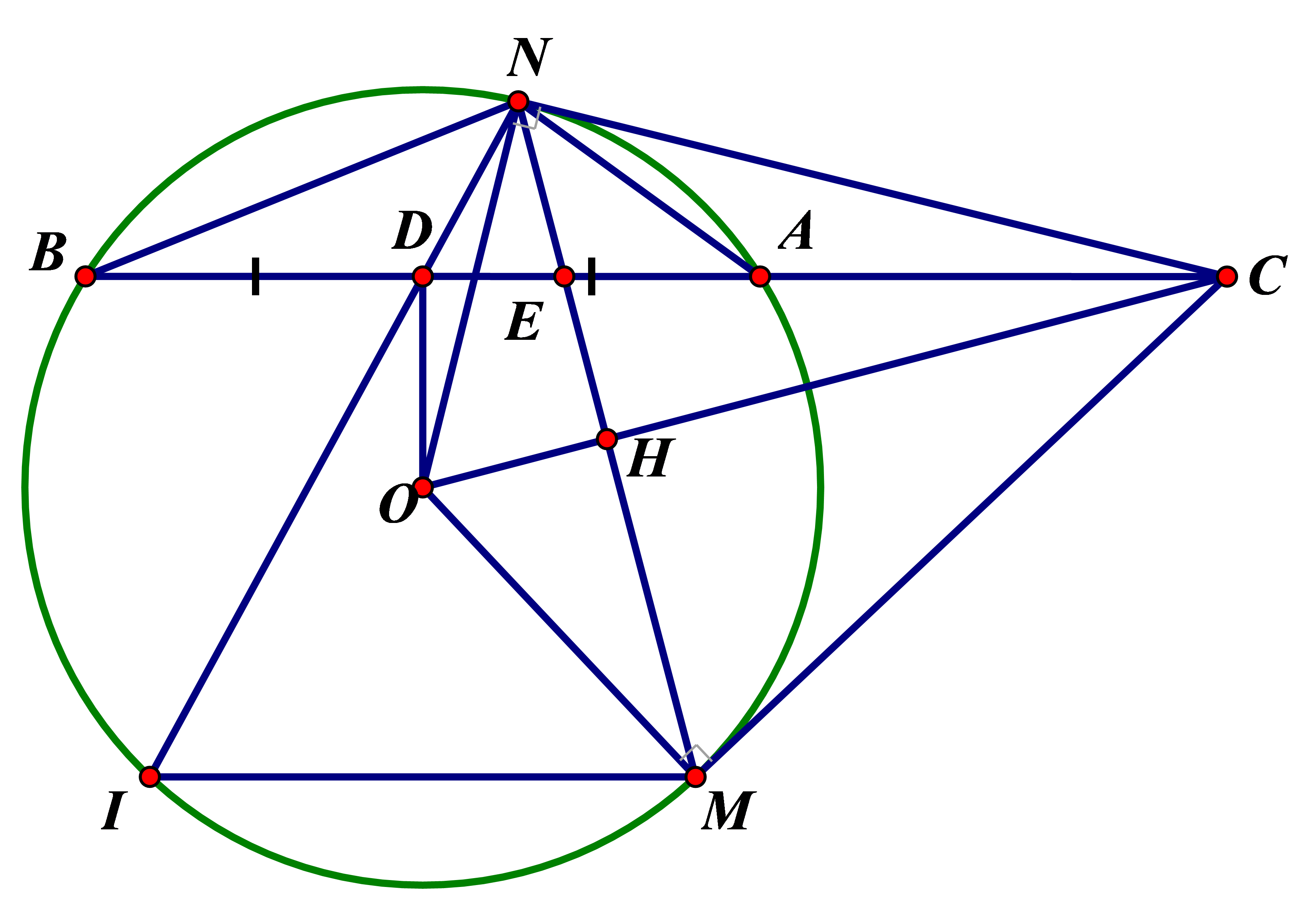
a) Ta có D là trung điểm của AB nên OD ⊥ AB (đường kính đi qua trung điểm của dây thì vuông góc với dây).
Ta có: = 90° (OD ⊥ AB)
= 90° (MC là tiếp tuyến của (O))
Xét tứ giác ABOC có += 90° + 90° = 180°
Suy ra tứ giác CMOD nội tiếp.
b) Xét ∆CAN và ∆CNB có:
là góc chung
(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung AN).
Suy ra ∆CAN đồng dạng ∆CNB (g.g)
Từ đó suy ra (điều phải chứng minh)
c) Ta có:
(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung NM)
(tứ giác CMOD nội tiếp)
Suy ra suy ra BC // IM.
d) Gọi H là giao điểm của MN và OC.
Ta có OM = ON = R.
CN = CM (tính chất hai tiếp tuyến cắt nhau).
Suy ra OC là trung trực của MN suy ra OC ⊥ MN.
Xét ∆CEH và ∆COD có:
là góc chung
= 90° (OD ⊥ AB và MN ⊥ OC)
Suy ra ∆CEH đồng dạng ∆COD (g.g)
Từ đó suy ra (1)
Xét tam giác ONC vuông tại N đường cao NH ta có:
NC2 = OH.OC
Mà NC2 = CA.CB (chứng minh trên)
Suy ra OH.OC = CA.CB (2)
Từ (1) và (2) ta được
CE.CD = CA.CB
Mà CB + CA = 2CA + AB = 2CA + 2DA
= 2(CA + DA) = 2CD
Thay vào trên ta được
(điều phải chứng minh)
