12 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 18

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 18

3338 lượt thi
12 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

Cho biểu thức $A = \frac{x + 5}{\sqrt{x} - 3}$ và $B = \frac{\sqrt{x} - 1}{\sqrt{x} + 3} + \frac{7 \sqrt{x} - 3}{x - 9}$

1) Tính giá trị của biểu thức khi x=25

Xem đáp án

1, Điều kiện để biểu thức xác định là $x \geq 0, x \neq 9.$

Khi $x = 25 (t m) \Rightarrow A = \frac{25 + 5}{\sqrt{25} - 3} = \frac{30}{2} = 15$

Vậy khi x=15 thì $A = 15.$

Câu 2:

2) Rút gọn biểu thức $B = \frac{\sqrt{x} - 1}{\sqrt{x} + 3} + \frac{7 \sqrt{x} - 3}{x - 9}$

Xem đáp án

2, Điều kiện : $x \geq 0, x \neq 9$

$\begin{array}{l} B = \frac{\sqrt{x} - 1}{\sqrt{x} + 3} + \frac{7 \sqrt{x} - 3}{x - 9} = \frac{\sqrt{x} - 1}{\sqrt{x} + 3} + \frac{7 \sqrt{x} - 3}{(\sqrt{x} - 3) (\sqrt{x} + 3)} \\ = \frac{(\sqrt{x} - 1) (\sqrt{x} - 3) + 7 \sqrt{x} - 3}{(\sqrt{x} - 3) (\sqrt{x} + 3)} \\ = \frac{x - 3 \sqrt{x} - \sqrt{x} + 3 + 7 \sqrt{x} - 3}{(\sqrt{x} - 3) (\sqrt{x} + 3)} = \frac{x + 3 \sqrt{x}}{(\sqrt{x} - 3) (\sqrt{x} + 3)} \\ = \frac{\sqrt{x} (\sqrt{x} + 3)}{(\sqrt{x} - 3) (\sqrt{x} + 3)} = \frac{\sqrt{x}}{\sqrt{x} - 3} \end{array}$

Câu 3:

3) Tìm giá trị nhỏ nhất của $\frac{A}{B}$

Xem đáp án

3, Điều kiện $x \geq 0, x \neq 9$

Ta có: $\frac{A}{B} = \frac{x + 5}{\sqrt{x} - 3} . \frac{\sqrt{x} - 3}{\sqrt{x}} = \frac{x + 5}{\sqrt{x}} = \sqrt{x} + \frac{5}{\sqrt{x}}$

Áp dụng BĐT Cô si cho hai số $\sqrt{x}, \frac{5}{\sqrt{x}}$ dương ta có: $\sqrt{x} + \frac{5}{\sqrt{x}} \geq 2 \sqrt{\sqrt{x} . \frac{5}{\sqrt{x}}} = 2 \sqrt{5}$

Dấu “=” xảy ra $\Leftrightarrow \sqrt{x} = \frac{5}{\sqrt{x}} \Leftrightarrow x = 5 (t m)$

Vậy với x=5 thì biểu thức $\frac{A}{B}$ đạt giá trị nhỏ nhất là $2 \sqrt{5}$

Câu 4:

1) Giải các phương trình sau:

x^{2} - 5 x + 4 = 0

Xem đáp án

a, $x^{2} - 5 x + 4 = 0$

Phương trình có dạng $a + b + c = 1 - 5 + 4 = 0$ nên có hai nghiệm phân biệt: $x_{1} = 1; x_{2} = 4.$

Vậy $S = \{1; 4\}$

Câu 5:

Giải các phương trình sau: b,

x^{4} + x^{2} - 6 = 0

Xem đáp án

b, $x^{4} + x^{2} - 6 = 0$

Đặt $x^{2} = t (t \geq 0)$ , khi đó ta có phương trình:

$\begin{array}{l} t^{2} + t - 6 = 0 \Leftrightarrow t^{2} + 3 t - 2 t - 6 = 0 \\ \Leftrightarrow t (t + 3) - 2 (t + 3) = 0 \Leftrightarrow (t - 2) (t + 3) = 0 \\ \Leftrightarrow [\begin{array}{l} t = 2 (t m) \Leftrightarrow [\begin{array}{l} x = \sqrt{2} \\ x = - \sqrt{2} \end{array} \\ t = - 3 (k t m) \end{array} \end{array}$

Vậy $S = \{- \sqrt{2}; \sqrt{2}\}$

Câu 6:

2, Giải hệ phương trình $\{\begin{cases} 2 x - y = 7 \\ x - 2 y = - 1 \end{cases}$

Xem đáp án

2, $\{\begin{cases} 2 x - y = 7 \\ x - 2 y = - 1 \end{cases} \Leftrightarrow \{\begin{cases} 4 x - 2 y = 14 \\ 2 x - y = 7 \end{cases} \Leftrightarrow \{\begin{cases} 3 x = 15 \\ y = 2 x - 7 \end{cases} \Leftrightarrow \{\begin{cases} x = 5 \\ y = 3 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất $(x; y) = (5; 3)$

Câu 7:

Cho phương trình $x^{2} + a x + b + 1 = 0$ với a,b là tham số. Tìm giá trị của để phương trình trên có 1 nghiệm $x_{1}, x_{2}$ thỏa mãn điều kiện $\{\begin{cases} x_{1} - x_{2} = 3 \\ x_{1}^{3} - x_{2}^{3} = 9 \end{cases}$

Xem đáp án

Phương trình $x^{2} + a x + b + 1 = 0$ có hai nghiệm

$x_{1}, x_{2} \Rightarrow Δ \geq 0 \Leftrightarrow a^{2} - 4 (b + 1) \geq 0 (*)$

Khi đó áp dụng định lý Viet ta có: $\{\begin{cases} x_{1} + x_{2} = - a \\ x_{1} x_{2} = b + 1 \end{cases}$

Ta có: $\begin{array}{l} +) {(x_{1} - x_{2})}^{2} = {(x_{1} + x_{2})}^{2} - 4 x_{1} x_{2} \Leftrightarrow 9 = a^{2} - 4 (b + 1) (1) \\ +) x_{1}^{3} - x_{2}^{3} = {(x_{1} - x_{2})}^{3} + 3 x_{1} x_{2} (x_{1} - x_{2}) \\ \Leftrightarrow 9 = 3^{2} + 3 (b + 1) .3 \Leftrightarrow - 18 = 9. (b + 1) \Leftrightarrow b + 1 = - 2 \Leftrightarrow b = - 3 \end{array}$

Thay b=-3 vào (1) ta có: $a^{2} - 4 (- 3 + 1) = 9 \Leftrightarrow a^{2} + 8 = 9 \Leftrightarrow a^{2} = 1 \Leftrightarrow a = \pm 1$

Thử lại $a^{2} = 1; b = - 3 \Rightarrow (*) \Leftrightarrow 1 - 4 (- 3 + 1) = 9 > 0 (t m)$

Vậy $(a, b) = (1; - 3)$ hoặc $(a, b) = (- 1; - 3)$

Câu 8:

Cho tứ giác ABCD nội tiếp đường tròn (O;R) và có hai đường chéo AC, BD vuông góc với nhau tại I (I khác O) . kẻ đường kính CE

a, Chứng minh tứ giác ABDE là hình thang cân

Xem đáp án

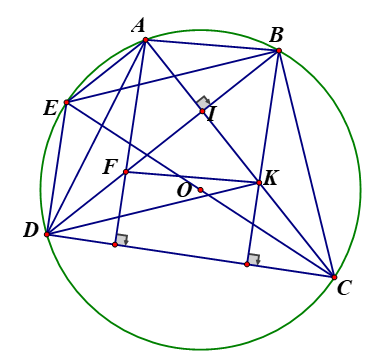
Cho tứ giác ABCD nội tiếp đường tròn (O;R) và có hai đường chéo AC, BD vuông góc (ảnh 1)

a, Ta có: $\hat{C A E} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow A E ⊥ A C$

Mà $B D ⊥ A C (g t) \Rightarrow A E / / B D$ (từ vuông góc đến song song)

$\to$ Tứ giác ABDE là hình thang (Tứ giác có 2 cạnh đối song song)

Ta có: $\hat{C D E} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow Δ C D E$ vuông tại D

Có: $\hat{C E D} = \hat{C B D}$ (hai góc nội tiếp cùng chắn cung CD)

$\Rightarrow 90^{0} - \hat{C E D} = 90^{0} - \hat{C B D} \Rightarrow \hat{D C E} = \hat{A C B}$

Mà $s d \overset{⏜}{D E} = s d \overset{⏜}{A B}$ (hai góc nôi tiếp cùng chắn hai cung bằng nhau)

$\Rightarrow D E = A B \Rightarrow D E + A E = A B + A E \Rightarrow A D = B E$

$\Rightarrow \hat{A B D} = \hat{E D B}$ (hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau)

$\to$ Tứ giác ABDE là hình thang cân (hình thang có 2 góc kề 1 đáy bằng nhau)

Câu 9:

b, Chứng minh $\sqrt{A B^{2} + C D^{2} + B C^{2} + D A^{2}} = 2 \sqrt{2} R$

Xem đáp án

b, Do ABDE là hình thang cân (cmt) $\Rightarrow A B = D E, A D = B E$

Khi đó ta có $A B^{2} + C D^{2} + B C^{2} + D A^{2} = D E^{2} + C D^{2} + B C^{2} + B E^{2}$

Ta có $\hat{C B E} = \hat{C D E} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn)

$\Rightarrow Δ B C E$ vuông tại B và tam giác CDE vuông tại D

Áp dụng định lý Pytago ta có:

$\begin{array}{l} \{\begin{cases} D E^{2} + C D^{2} = C E^{2} = {(2 R)}^{2} = 4 R^{2} \\ B C^{2} + B E^{2} = E C^{2} = {(2 R)}^{2} = 4 R^{2} \end{cases} \Rightarrow D E^{2} + C D^{2} + B C^{2} + B E^{2} = 8 R^{2} \\ \Rightarrow A B^{2} + C D^{2} + B C^{2} + D A^{2} = 8 R^{2} \Leftrightarrow \sqrt{A B^{2} + C D^{2} + B C^{2} + D A^{2}} = \sqrt{8 R^{2}} = 2 \sqrt{2} R \end{array}$

Câu 10:

c, Từ A và B kẻ các đường thẳng vuông góc với CD lần lượt cắt BD tại F, cắt tại K. Tứ giác ABKF là hình gì ?

Xem đáp án

c, Xét $Δ B C D$ có K là trực tâm (giao của hai đường cao) $\Rightarrow D K ⊥ B C .$

Mà $B E ⊥ B C (\hat{C B E} = 90^{0})$ $\Rightarrow D K / / B E$ (từ vuông góc đến song song)

Ta có: $\{\begin{cases} B K ⊥ C D \\ D E ⊥ C D (\hat{C D E} = 90^{0}) \end{cases} \Rightarrow B K / / D E$ ( từ vuông góc đến song song)

Ta có: $\{\begin{cases} A F ⊥ C D (g t) \\ D E ⊥ C D (\hat{C D E} = 90^{O}) \end{cases} \Rightarrow A F / / D E$ ( từ vuông góc đến song song)

Xét tứ giác ADEF có $\{\begin{cases} A F / / D E \\ A E / / D F (A E / / B D) \end{cases} \Rightarrow$ Tứ giác là hình bình hành ADEF

$\Rightarrow A F = D E (2)$

Từ (1) và (2) $\Rightarrow B K = A F (= D E)$

Xét tứ giác ABKF có: $\{\begin{cases} A F ⊥ C D (g t) \\ B K ⊥ C D (g t) \end{cases} \Rightarrow A F / / B K$ và $A F = B K (c m t)$

Tứ giác ABKF là hình bình hành.

Câu 11:

1. a, Tìm nghiệm nguyên của phương trình: $y^{3} = x^{3} + x^{2} + x + 1$

Xem đáp án

a, Tìm nghiệm nguyên…..

TH1: Xét $x^{2} + x > 0 \Leftrightarrow x (x + 1) > 0 \Leftrightarrow [\begin{array}{l} x > 0 \\ x < - 1 \end{array},$ từ đó ta có $2 (x^{2} + x) > 0$

$\begin{array}{l} \Rightarrow x^{3} + x^{2} + x + 1 < x^{3} + x^{2} + x + 1 + 2 (x^{2} + x) = x^{3} + 3 x^{2} + 3 x + 1 = {(x + 1)}^{3} \\ \Rightarrow x^{3} < x^{3} + x^{2} + x + 1 < {(x + 1)}^{3} \end{array}$

Theo đề bài ta có: $y^{3} = x^{3} + x^{2} + x + 1$

$\Rightarrow x^{3} < y^{3} < {(x + 1)}^{3},$ lại có $x, y \in ℤ (g t)$

$\Rightarrow$ Không tồn tại số nguyên $x, y$ thỏa mãn $x^{3} < y^{3} < {(x + 1)}^{3}$

TH2: Xét $- 1 \leq x \leq 0,$ lại có $x \in ℤ (g t) \Rightarrow [\begin{array}{l} x = - 1 \\ x = 0 \end{array}$

+) Với $x = - 1 \Rightarrow y^{3} = {(- 1)}^{3} + {(- 1)}^{2} - 1 + 1 = 0 \Rightarrow y = 0 (t m)$

+)Với $x = 0 \Rightarrow y^{3} = 1 \Leftrightarrow y = 1 (t m)$

Vậy phương trình có các cặp nghiệm nguyên là $(x; y) = \{(- 1; 0); (0; 1)\}$

Câu 12:

b, Cho các số nguyên a, b, c thỏa mãn $a b + b c + c a = 1.$

Chứng minh rằng: $A = (1 + a^{2}) (1 + b^{2}) (1 + c^{2})$ là một số chính phương

Xem đáp án

b, Theo đề bài ta có: $a b + b c + c a = 1$

$\Rightarrow 1 + a^{2} = a b + b c + c a + a^{2} = b (a + c) + a (c + a) = (a + c) (a + b)$

Tương tự ta có: $\{\begin{cases} 1 + b^{2} = (b + a) (b + c) \\ 1 + c^{2} = (c + a) (c + b) \end{cases}$

$\begin{array}{l} \Rightarrow A = (1 + a^{2}) (1 + b^{2}) (1 + c^{2}) = (a + c) (a + b) (b + a) (b + c) (c + a) (c + b) \\ = {(a + b)}^{2} {(a + c)}^{2} {(b + c)}^{2} = {[(a + b) (a + c) (b + c)]}^{2} (a, b, c \in ℤ) \end{array}$

Vậy A là một số chính phương.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 18

Danh sách câu hỏi

Bài thi liên quan