10 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 26

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 26

4736 lượt thi
10 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

a, Giải phương trình: $\sqrt{4 x^{2} - 4 x + 9} = 3$

Xem đáp án

$\begin{array}{l} a) \sqrt{4 x^{2} - 4 x + 9} = 3 \Leftrightarrow 4 x^{2} - 4 x + 9 = 9 \\ \Leftrightarrow 4 x (x - 1) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x = 1 \end{array} \end{array}$

Vậy $S = \{0; 1\}$

Câu 2:

b,Giải hệ phương trình: $\{\begin{cases} 3 x - y = 5 \\ 2 y - x = 0 \end{cases}$

Xem đáp án

$b) \{\begin{cases} 3 x - y = 5 \\ 2 y - x = 0 \end{cases} \Leftrightarrow \{\begin{cases} 3 x - y = 5 \\ 2 y - x = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 y \\ 3 x - y = 5 \end{cases} \Leftrightarrow \{\begin{cases} 5 y = 5 \\ x = 2 y \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = 1 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất $(x; y) = (2; 1)$

Câu 3:

a,Cho hai đường thẳng $(d_{1}) : y = 2 x - 5$ và $(d_{2}) : y = 4 x - m$ (m là tham số). Tìm tất cả các giá trị của tham số m để $(d_{1})$ và $(d_{2})$ cắt nhau tại một điểm trên trục hoành Ox

Xem đáp án

a, Do $2 \neq 4$ nên $(d_{1})$ và luôn cắt nhau.

Giao điểm của $(d_{1})$ với trục $(d_{2})$ là điểm $M (\frac{5}{2}; 0)$

Giao điểm của $(d_{2})$ với trục Ox là điểm $N (\frac{m}{4}; 0)$

Để $(d_{1})$ và $(d_{2})$ cắt nhau tại một điểm trên trục Ox thì $\frac{m}{4} = \frac{5}{2} \Leftrightarrow m = 10$

Vậy m=10 thỏa mãn đề bài.

Câu 4:

b, Rút gọn biểu thức: $P = (\frac{\sqrt{x}}{3 + \sqrt{x}} + \frac{2 x}{9 - x}) : (\frac{\sqrt{x} - 1}{x - 3 \sqrt{x}} - \frac{2}{\sqrt{x}})$ (với $x > 0, x \neq 9, x \neq 25)$

Xem đáp án

$\begin{array}{l} b) P = [\frac{\sqrt{x} (3 - \sqrt{x}) + 2 x}{(3 + \sqrt{x}) (3 - \sqrt{x})}] : [\frac{\sqrt{x} - 1 - 2 (\sqrt{x} - 3)}{\sqrt{x} . (\sqrt{x} - 3)}] \\ = \frac{3 \sqrt{x} + x}{(3 + \sqrt{x}) (3 - \sqrt{x})} : \frac{5 - \sqrt{x}}{\sqrt{x} . (\sqrt{x} - 3)} \\ = \frac{\sqrt{x} . (3 + \sqrt{x})}{(3 + \sqrt{x}) (3 - \sqrt{x})} . \frac{\sqrt{x} . (\sqrt{x} - 3)}{5 - \sqrt{x}} = \frac{x}{\sqrt{x} - 5} \end{array}$

Vậy $P = \frac{x}{\sqrt{x} - 5}$ với $x > 0, x \neq 9, x \neq 25$

Câu 5:

a, Theo kế hoạch, một xưởng may phải may xong 360 bộ quần áo trong một thời gian quy định. Đến khi thực hiện, mỗi ngày xưởng đã may nhiều hơn 4 bộ quần áo so với số bộ quần áo phải may trong một ngày theo kế hoạch. Vì thế xưởng đã hoàn thành kế hoạch trước 1 ngày. Hỏi theo kế hoạch, mỗi ngày xưởng phải may bao nhiêu bộ quần áo?

Xem đáp án

a, Gọi x là số bộ quần áo mà xưởng may phải may trong một ngày theo kế hoạch

$(0 < x < 360, x \in ℕ)$

Suy ra số ngày mà xưởng may phải hoàn thành theo kế hoạch là $\frac{360}{x}$ (ngày)

Số bộ quần áo mà xưởng thực tế đã may trong mọt ngày là x + 4 (bộ)

Số ngày thực tế mà xưởng may đã hoàn thành là $\frac{360}{x + 4}$ (ngày)

Theo bài ta có phương trình: $\frac{360}{x + 4} + 1 = \frac{360}{x} (1)$

$(1) \Leftrightarrow x^{2} + 4 x - 1440 = 0 \Leftrightarrow [\begin{array}{l} x = 36 (t m) \\ x = - 40 (k t m) \end{array}$

Vậy theo kế hoạch mỗi ngày xưởng phải may 36 bộ quần áo

Câu 6:

b,Cho phương trình: $x^{2} - (2 m + 1) x - 3 = 0$ (m là tham số). Chứng minh rằng phương trình đã cho luôn có hai nghiệm phân biệt $x_{1}, x_{2}$ với mọi m Tìm các giá trị của m sao cho $|x_{1}| - |x_{2}| = 5$ và $x_{1} < x_{2}$

Xem đáp án

b, Xét phương trình $x^{2} - (2 m + 1) x - 3 = 0$ có $Δ = {[- (2 m + 1)]}^{2} - 4. (- 3) = {(2 m + 1)}^{2} + 12 > 0$

$\Rightarrow Δ > 0 \Rightarrow$ phương trình đã cho luôn có hai nghiệm phân biệt $x_{1}, x_{2}$ với mọi x

Theo định lý Vi-et ta có: $\{\begin{cases} x_{1} + x_{2} = 2 m + 1 \\ x_{1} x_{2} = - 3 \end{cases}$

Vì $x_{1} x_{2} = - 3 < 0$ nên $x_{1}, x_{2}$ trái dấu nhau mà $x_{1} < x_{2}$ nên $x_{1} < 0 & x_{2} > 0$

Khi đó ta có $|x_{1}| - |x_{2}| = 5 \Leftrightarrow x_{1} - x_{2} = 5 \Leftrightarrow - (x_{1} + x_{2}) = 5 \Leftrightarrow x_{1} + x_{2} = - 5$

$\Leftrightarrow 2 m + 1 = - 5 \Leftrightarrow m = - 3$

Vậy $m = - 3$ thỏa mãn đề bài.

Câu 7:

Từ điểm A nằm ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Trên nửa mặt phẳng bờ lầ đường thẳng AO chứa điểm B vẽ cát tuyến AMN với đường tròn (O) ( $A M < A N, M N$ không đi qua O). Gọi I là trung điểm của MN

a, Chứng minh: Tứ giác AIOC là tứ giác nội tiếp

Xem đáp án

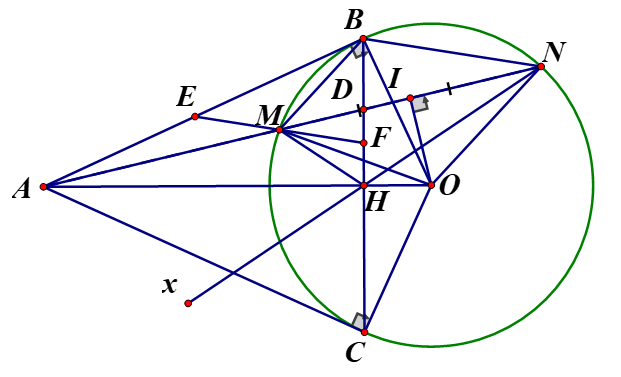
Từ điểm A nằm ngoài đường tròn (O) kẻ hai tiếp tuyến AB, AC với đường tròn (ảnh 1)

Vì I là trung điểm của MN nên $O I ⊥ M N \Rightarrow \hat{O I A} = 90^{0}$

Vì AC là tiếp tuyến của đường tròn Otại C nên $A C ⊥ O C \Rightarrow \hat{O C A} = 90^{0}$

Xét tứ giác AIOC có: $\hat{A I O} + \hat{A C O} = 90^{0} + 90^{0} = 180^{0}$

Mà hai góc này ở vị trí đối nhau nên suy ra tứ giác AIOC là tứ giác nội tiếp

Câu 8:

b, Gọi H là giao điểm của AO và BC. Chứng minh $A H . A O = A M . A N$ và tư giác $M N O H$ là tứ giác nội tiếp

Xem đáp án

b, Vì AB, AC là hai tiếp tuyến của đường tròn (O) $\Rightarrow A B = A C$ và AO là tia phân giác của $\hat{B A C} \Rightarrow Δ A B C$ cân tại O có AO là đường phân giác nên AO cũng là đường cao của $Δ A B C \Rightarrow A O ⊥ B C$ hay $A H ⊥ B C .$

Vì AB là tiếp tuyến của đường tròn (O) tại B nên $A B ⊥ O B \Rightarrow \hat{O B A} = 90^{0} \Rightarrow Δ A B O$ vuông tại B

Xét $Δ A B O$ vuông tại B có BH là đường cao $\Rightarrow A B^{2} = A H . A O (1)$

Xét đường tròn (O) có $\hat{A B M}$ là góc tạo bởi tiếp tuyến và dây cung chắn cung $B M, \hat{A N B}$ là góc nội tiếp chắn cung BM $\Rightarrow \hat{A B M} = \hat{A N B}$

Xét $Δ A B M$ và $Δ A N B$ có $\hat{A B M} = \hat{A N B}$ và $\hat{B A N}$ chung

$\Rightarrow Δ A B M ~ Δ A N B (g . g) \Rightarrow \frac{A B}{A N} = \frac{A M}{A B} \Rightarrow A B^{2} = A M . A N (2)$

Từ (1) và (2) $\Rightarrow A H . A O = A M . A N$

+Vì $A H . A O = A M . A N \Rightarrow \frac{A H}{A N} = \frac{A M}{A O}$ và $\hat{N A O}$ chung

$\Rightarrow Δ A M H ~ Δ A O N (c g c) \Rightarrow \hat{A H M} = \hat{A N O}$

Mà $\hat{A H M} + \hat{M H O} = 180^{0} ($ kề bù) $\Rightarrow \hat{A N O} + \hat{M H O} = 180^{0}$

Hay $\hat{M N O} + \hat{M H O} = 180^{0}$

Xét tứ giác MNOH có $\hat{M N O} + \hat{M H O} = 90^{0} + 90^{0} = 180^{0}$

$\Rightarrow$ Tứ giác $M N O H$ là tứ giác nội tiếp.

Câu 9:

c, Qua M kẻ đường thẳng song song với BN cắt AB và BC theo thứ tự tại E và F. Chứng minh rằng M là trung điểm của EF

Xem đáp án

c, Gọi Hx là tia đối của tia HN

Vì tứ giác MNOH nội tiếp $\Rightarrow \hat{N H O} = \hat{N M O}$

Mà (do $Δ M N O$ cân tại O) $\Rightarrow \hat{N H O} = \hat{M N O}$

Do $\hat{A H M} = \hat{A N O}$ (cmt) hay $\hat{A H M} = \hat{M N O} \Rightarrow \hat{A H M} = \hat{N H O}$

Vì $\hat{A H M} + \hat{M H B} = 90^{0}$ và $\hat{N H O} + \hat{N H B} = 90^{0} \Rightarrow \hat{M H B} = \hat{N H B}$

$\Rightarrow H B$ là tia phân giác của $\hat{M H N}$

Gọi BC cắt AN tại D $\Rightarrow H D$ là tia phân giác của $\hat{M H N}$

Vì $\hat{N H O} = \hat{A H x}$ (đối đỉnh) và $\hat{A H M} = \hat{N H O} \Rightarrow \hat{A H M} = \hat{A H x}$

$\Rightarrow H A$ là tia phân giác của $\hat{M H x}$

Xét $Δ M H N$ có HD là đường phân giác trong tại đỉnh H $\Rightarrow \frac{H M}{H N} = \frac{D M}{D N} (3)$

Xét $Δ M H N$ có HA là đường phân giác ngoài tại đỉnh $H \Rightarrow \frac{H M}{H N} = \frac{A M}{A N} (4)$

Từ (3) (4) $\Rightarrow \frac{D M}{D N} = \frac{A M}{A N}$

Ta có: $E M / / B N \Rightarrow \frac{E M}{B N} = \frac{A M}{A N}$

Ta có: $B N / / M F \Rightarrow \frac{D M}{D N} = \frac{M F}{B N}$

Mà $\frac{D M}{D N} = \frac{A M}{A N} \Rightarrow \frac{E M}{B N} = \frac{F M}{B N} \Rightarrow M E = M F$ $\Rightarrow M$ là trung điểm của EF

Câu 10:

Cho các số dương a,b,c thỏa mãn điều kiện: a + b +c = 2019

Tìm giá trị nhỏ nhất của biểu thức: $P = \sqrt{2 a^{2} + a b + 2 b^{2}} + \sqrt{2 b^{2} + b c + 2 c^{2}} + \sqrt{2 c^{2} + c a + 2 a^{2}}$

Xem đáp án

Ta có:

$\begin{array}{l} 4 (2 a^{2} + a b + 2 b^{2}) = 5 (a^{2} + 2 a b + b^{2}) + 3 (a^{2} - 2 a b + b^{2}) \\ = 5 (a^{2} + b^{2}) + 3 {(a - b)}^{2} \geq 5 {(a + b)}^{2}, d o {(a - b)}^{2} \geq 0 \end{array}$

Vì a,b dương nên:

$2 \sqrt{2 a^{2} + a b + 2 b^{2}} \geq 5 (a + b) \Leftrightarrow \sqrt{2 a^{2} + a b + 2 b^{2}} \geq \frac{\sqrt{5}}{2} (a + b) (1)$

Dấu $" = "$ xảy ra khi a= b

Chứng minh tương tự để có:

$\sqrt{2 b^{2} + b c + 2 c^{2}} \geq \frac{\sqrt{5}}{2} (b + c) (2),$

Dấu “=” xảy ra khi $b = c$

Và $\sqrt{2 c^{2} + c a + 2 a^{2}} \geq \frac{\sqrt{5}}{2} (c + a) (3),$ Dấu $" = "$ xảy ra khi c=a

Cộng vế theo vế các bất đẳng thức $(1), (2), (3)$ ta được:

$\sqrt{2 a^{2} + a b + 2 b^{2}} + \sqrt{2 b^{2} + b c + 2 c^{2}} + \sqrt{2 c^{2} + c a + 2 a^{2}} \geq \frac{\sqrt{5}}{2} .2 (a + b + c) = 2019 \sqrt{5}$

Dấu $" = "$ xảy ra $\Leftrightarrow \{\begin{cases} a = b = c \\ a + b + c = 2019 \end{cases} \Leftrightarrow a = b = c = 673$

Vậy $P_{\min} = 2019 \sqrt{5} \Leftrightarrow a = b = c = 673$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 26

Danh sách câu hỏi

Bài thi liên quan