Thứ ba, 30/04/2024
Đăng ký Đăng nhập
IMG-LOGO
Trang chủ Lớp 9 Toán Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 19

  • 3355 lượt thi

  • 15 câu hỏi

  • 45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

    1, Giải phương trình: 2x2−7x+6=0
Xem đáp án

     1, GPT: 2x2−7x+6=0

Ta có: Δ=b2−4ac=−72−4.2.6=1>0

→Phương trình có hai nghiệm phân biệt x1=7+12.2=2x2=7−12.2=32

Vậy tập nghiệm của hệ phương trình là S=32;2

Câu 2:

2, Giải hệ phương trình : 2x−3y=−53x+4y=18
Xem đáp án

2, 2x−3y=−53x+4y=18⇔6x−9y=−156x+8y=3617y=51x=3y−52⇔y=3x=2

Vậy hệ phương trình có nghiệm duy nhất x;y=2;3

Câu 3:

3, Giải phương trình: x4+7x2−18=0
Xem đáp án

3, x4+7x2−18=0 

Đặt x2=tt≥0,  khi đó ta có phương trình: t2+7t−18=0    (1)

Ta có: Δ=72+4.18=121>0

 ⇒1 có hai nghiệm phân biệt t1=−7+1212=2(tm)t2=−7−1212=−7−112=−9(ktm)

Với t=2⇒x2=2⇔x=±2

Vậy phương trình đã cho có tập nghiệm S=−2;2

Câu 4:

a,Vẽ đồ thị của hai hàm số y=−12x2,y=2x−1  trên cùng một mặt phẳng tọa độ
Xem đáp án

a, Học sinh tự vẽ các đồ thị

Câu 5:

b, Tìm các tham số thực m  để hai đường thẳng y=m2+1x+m  và  y=2x−1song song với nhau.
Xem đáp án

b, Hai đường thẳng: y=m2+1x+m  và  y=2x−1 song song với nhau

⇔m2+1=2m≠−1⇔m2=1m≠−1⇒m=1m=−1m≠−1⇔m=1

 

Vậy m=1 thỏa mãn bài toán

Câu 6:

c, Tìm các số thực x  để biểu thức M=3x−5−1x2−43
Xem đáp án

c, Biểu thức M đã cho xác định ⇔3x−5≥0x2−4≠0⇔3x≥5x2≠4⇔x≥53x≠±2⇔x≥53x≠2

Vậy biểu thức M  xác định khi và chỉ khi x≥53,x≠2

Câu 7:

Cho tam giác MNP  vuông tại N  có MN=4a,NP=3a với Tính theo a  diện tích xung quanh của hình nón tạo bởi tam giác MNP quay quanh đường thẳng MN 
Xem đáp án

          Khi xoay tam giác MNP  vuông tại N quanh đường thẳng MN ta được hình nón có chiều cao h=MN=4a  và bán kính đáy R=NP=3a.

Áp dụng định lý Pyta go trong tam giác vuông MNP ta có: 

MP2=MN2+NP2=4a2+3a2=25a2⇒MN=25a2=5a(Do...a>0)

Do đó hình nón có độ dài đường sinh là l=MP=5a

Vậy diện tích xung quanh của hình nón là Sxq=πRl=π.3a.5a=15πa2

Câu 8:

Cho x1,x2  là hai nghiệm của phương trình x2−3x+1=0.  Hãy lập một phương trình bậc hai một ẩn có hai nghiệm là 2x1−x22  và 2x2−x12
Xem đáp án

Phương trình x2−3x+1=0  có 2 nghiệm x1,x2(gt)  nên áp dụng định lý Viet ta có:

x1+x2=3x1x2=1

Xét các tổng và tích sau:

P=2x1−x222x2−x12=4x1x2−2x13−2x23+x1x22=4x1x2−2x13+x23+x1x22=4x1x2−2x1+x23−3x1x2x1+x2+x1x22=4.1−2.33−3.1.3+12=−31

S=2x1−x22+2x2−x12=2x1+x2−x12+x22=2x1+x2−x1+x22−2x1x2=2.3−32−2.1=−1

Ta có:S2=−12=1≥4P=−124

⇒2x1−x22 và 2x2−x12  là hai nghiệm của phương trình

X2−SX+P=0⇔X2+X−31=0

                             

Câu 9:

Bác B vay ở một ngân hàng triệu động để sản xuất trong thời hạn 1 năm. Lẽ ra đúng một năm sau bác phải trả cả tiền vốn và lãi, song, bác đã được ngân hàng cho kéo dài thời hạn thêm 1 năm nữa, số tiền lãi của năm đầu được tính gộp vào tiền vốn để tính lãi năm sau và lãi suất vẫn như cũ. Hết 2 năm, bác B phải trả tất cả triệu đồng. Hỏi lãi suất cho vay của ngân hàng đó là bao nhiêu phần trăm trong một năm
Xem đáp án

Gọi lãi suất cho vay của ngân hàng đó là (%/năm) (ĐK: x>0)

Số tiền lãi bác B phải trả sau 1 năm gửi 100 triệu đồng là 100.x%=x  (triệu đồng)

→Số tiền bác B phải trả sau 1 năm là 100+x  (triệu đồng)

Do số tiền lãi của năm đầu được tính gộp vào tiền vốn để tính lãi năm sau nên số tiền lãi bác B phải trả sau 2 năm là 100+xx%=100+xx100  (triệu đồng)

Hết 2 năm bác B phải trả tất cả là triệu đồng nên ta có phương trình:

100+x+100+xx100=121⇔10000+100x+100x+x2=12100⇔x2+200x−2100=0⇔x2−10x+210x−2100=0⇔xx−10+210(x−10)=0⇔x−10x+210=0⇔x=10(tm)x=−210(ktm)

Vậy lãi suất của ngân hàng đó là10% /năm

Câu 10:

Rút gọn biểu thức P=a+a1+a.a−3a+2a−2a≥0,a≠4
Xem đáp án

Với  a≥0,a≠4 thì

P=a+a1+a.a−3a+2a−2=a1+a1+a.a−2a−a+2a−2=a.a.a−2−a−2a−2=a.a−1a−2a−2=a.a−1=a−a

 

Câu 11:

Tìm các số thực x và y  thỏa mãn 4x2−xy=2y2−3xy=−2
Xem đáp án

4x2−xy=2(1)y2−3xy=−2(2)

Lấy (1) cộng (2) vế theo vế ta được:

4x2−xy+y2−3xy=0⇔4x2−4xy+y2=0⇔2x−y2=0⇔2x−y=0⇔y=2x

Thay y=2x vào (2) ta được:

2x2−3x.2x=−2⇔4x2−6x2=−2⇔−2x2=−2⇔x2=1⇔x=1⇒y=x=−1⇒y=−2

Vậy hệ có nghiệm x;y=1;2;−1;−2

Câu 12:

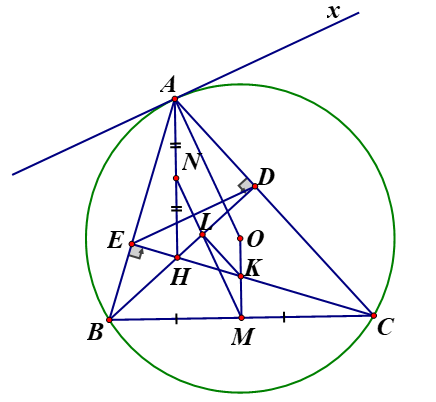
Cho tam giác ABC  nội tiếp đường tròn (O) có hai đường cao BD và CE cắt nhau tại trực tâm H. Biết ba góc CAB^,ABC^,BAC^  đều là góc nhọn

a, Chứng minh bốn điểm B,C,D,E  cùng thuộc một đường tròn.
Xem đáp án
Cho tam giác ABC  nội tiếp đường tròn (O) có hai đường cao BD và CE cắt nhau tại trực tâm H. (ảnh 1)

a, Ta có: BD⊥AC⇒BDC^=900CE⊥AB⇒CEB^=900

Tứ giác BEDC có BDC^=BEC^=900  nên nó là tứ giác nội tiếp (tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau).

Suy ra 4 điểm B,D,C,E  cùng thuộc một đường tròn

Câu 13:

b, Chứng minh vuông góc DE với OA
Xem đáp án

Kẻ tiếp tuyến Ax với đường tròn (O) tại A⇒Ax⊥AO  (tính chất tiếp tuyến )

Ta có:CAx^=CBA^ (góc tạo bởi tiếp tuyến dây cung và góc nội tiếp cùng chắn AC⏜)  (1)

Do tứ giác BEDC  nội tiếp (cmt) ⇒CBA^=EDA^ (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện ) (2)

Từ (1) và (2) suy ra CAx^=EDA^=CBA^

Mà hai góc này ở vị trí so le trong nên DE//Ax  mà Ax⊥AO(cmt)⇒DE⊥AO(dfcm)

Câu 14:

c, Cho M,N lần lượt là trung điểm của hai đoạn thẳng BC, AH Cho K,L lần lượt là giao điểm của hai đường thẳng OM  và CE, MN và BD. Chứng minh KL song song với AC
Xem đáp án

c,Kẻ đường kính AI  của đường tròn (O) , gọi giao điểm của MN và ED  là P

Xét đường tròn (O) ta có: ACI^=900,ABI^=900  (các góc nội tiếp chắn nửa đường tròn)

Suy ra  CI⊥AC,BI⊥AB lại có: BD⊥AC,CE⊥AB(gt)  nên BH//CI,CH//BI

Xét tứ giác BHCI  có: BH//CICH//BI⇒BHCI  là hình bình hành có M là trung điểm BC nên M cũng là trung điểm của HI

Xét ΔHIA  có: M là trung điểm của HI, N là trung điểm của AH

⇒MN là đường trung bình của ΔHAI⇒MN//AI  (tính chất đường trung bình)

Theo câu b) ta có: AO⊥DE⇒MN⊥DE  tại P

Xét tam giác PLD vuông có PLD^=900−PDL^(3)

Xét đường tròn (O) có M là trung điểm của  BC⇒OM⊥BC hay là đường trung trực của BC

Mà K∈OM⇒KB=KC

Xét ΔKBC  cân tại K có KM là đường cao nên cũng là đường phân giác ΔKBC

⇒BKM^=MKC^ (tính chất đường phân giác)

Xét ΔKMC  vuông tại M có  MKC^=900−KCM^⇒BKM^=900−KCM^(4)

Lại có: EDB^=ECB^  (do tứ giác BEDC nội tiếp) hay PDL^=KCM^(5)

Từ (3) (4) (5) suy ra BKM^=PLD^  mà PLD^=BLM^  (hai góc đối đỉnh ) nên BLM^=BKM^

Xét tứ giác BLKM có BLM^=BKM^  nên hai đỉnh L, K kề nhau cùng nhìn cạnh BM  dưới các góc bằng nhau, do đó tứ giác BLKM  là tứ giác nội tiếp

Suy ra BLM^+BMK^=1800⇔BLK^=1800−900=900

Hay KL⊥BD   mà AC⊥BD(gt)⇒KL//AC

Câu 15:

Cho ba số thực a,b,c. Chứng minh rằng

         a2−bc3+b2−ca+c2−ab3≥3a2−bcb2−cac2−ab

Xem đáp án

Đặt x=a2−bc,y=b2−ca,z=c2−ab

Bất đẳng thức cần chứng minh trở thành x3+y3+z3≥3xyz

Ta có:

x3+y3+z3−3xyz=x3+y3−3xyz+z3=x+y3−3xyx+y−3xyz+z3=x+y3+z3−3xyx+y+z=x+y+zx+y2−x+yz+z2−3xyx+y+z=x+y+zx2+2xy+y2−xz−yz+z2−3xy=x+y+zx2+y2+z2−xy−yz−xz

Dễ thấy

x2+y2+z2−xy−yz−xz=12x2−2xy+y2+y2−2yz+z2+z2−2zx+x2=12x−y2+y−z2+z−x2≥0∀x,y,z

Do đó ta đi xét dấu x+ y +z 

Ta có: 

x+y+z=a2−bc+b2−ca+c2−ab

=a2+b2+c2−ab−bc−ca=12a−b2+b−c2+c−a2≥0,∀a,b,c

Suy ra x+y+z≥0⇒x+y+zx2+y2+z2−xy−yz−zx≥0

⇒x3+y3+z3≥3xyz

hay a2−bc3+b2−ca3+c2−ab3≥3a2−bcb2−cac2−ab(dfcm)

dấu "="  xảy ra khi và chỉ khi  a=b=c

           

Bắt đầu thi ngay

Bài thi liên quan