29 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 3

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 3

3337 lượt thi
29 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giá trị của tham số m để đường thẳng $d : y = m x + 1$ song song với đường thẳng $y = 2 x - 3$ là:

A. $m = - 3$

B. $m = - 1$

C. $m = 1$

D. $m = 2$

Xem đáp án

Chọn đáp án án D

Câu 2:

Tổng hai nghiệm của phương trình : $x^{2} - 4 x + 3 = 0$ bằng:

A. -4

B. 4

C. 3

D. -3

Xem đáp án

Chọn đáp án B

Câu 3:

Giá trị nào của x dưới đây là nghiệm của phương trình

x^{2} + x - 2 = 0 ?

A. x=4

B. x= 3

C. x=2

D. x=1

Xem đáp án

Chọn đáp án D

Câu 4:

Đường thẳng

y = 4 x - 5

có hệ số góc bằng:

A. -5

B. 4

C. -4

D. 5

Xem đáp án

Chọn đáp án B

Câu 5:

Cho biết x=1 là một nghiệm của phương trình $x^{2} + b x + c = 0.$ Khi đó ta có:

A. $b + c = 1$

B. $b + c = 2$

C. $b + c = - 1$

D. $b + c = 0$

Xem đáp án

Chọn đáp án C

Câu 6:

Tất cả các giá trị của x để biểu thức $\sqrt{x - 3}$ có nghĩa là:

A. $x \geq 3$

B. $x \leq 3$

C. x<3

D. x > 3

Xem đáp án

Chọn đáp án A

Câu 7:

Cho tam giác ABC có $A B = 3 c m, A C = 4 c m, B C = 5 c m .$ Phát biểu nào sau đây là đúng ?

A. Tam giác ABC vuông

B. Tam giác ABC đều

C. Tam giác ABC vuông cân

D. Tam giác ABC cân

Xem đáp án

Chọn đáp án A

Câu 8:

Giá trị của tham số m để đường thẳng $y = (2 m + 1) x + 3$ đi qua điểm $A (- 1; 0)$ là:

A. m=-2

B. m= 1

C. m=-1

D. m=2

Xem đáp án

Chọn đáp án B

Câu 9:

Căn bậc hai số học của 144 là:

A. 13

B. -12

C 12 và -12

D. -13

Xem đáp án

Chọn đáp án D

Câu 10:

Với $x < 2$ thì biểu thức $\sqrt{{(2 - x)}^{2}} + x - 3$ có giá trị bằng:

A. -1

B. $2 x - 5$

C. 5-2x

D. 1

Xem đáp án

Chọn đáp án A

Câu 11:

Giá trị của biểu thức $\frac{3 + \sqrt{3}}{\sqrt{3} + 1}$ bằng

A. 3

B. $\frac{1}{\sqrt{3}}$

C. $\frac{1}{3}$

D. $\sqrt{3}$

Xem đáp án

Chọn đáp án D

Câu 12:

Hệ phương trình $\{\begin{cases} x - y = 1 \\ x + 2 y = 7 \end{cases}$ có nghiệm là $(x_{0}; y_{0}) .$ Giá trị của biểu thức $x_{0} + y_{0}$ bằng:

A. 1

B. -2

C . 5

D. 4

Xem đáp án

Chọn đáp án C

Câu 13:

Cho tam giác ABC vuông tại A, có $B C = 4 c m, A C = 2 c m .$ Tính $\sin \hat{A B C}$

A. $\frac{\sqrt{3}}{2}$

B. $\frac{1}{2}$

C. $\frac{1}{3}$

D. $\frac{\sqrt{3}}{3}$

Xem đáp án

Chọn đáp án B

Câu 14:

Tam giác ABC cân tại B có $\hat{A B C} = 120^{0}, A B = 12 c m$ và nội tiếp đường tròn (O). Bán kính của đường tròn (O) bằng:

A. 10cm

B. 9cm

C. 8cm

D. 12cm

Xem đáp án

Chọn đáp án D

Câu 15:

Biết rằng đường thẳng $y = 2 x + 3$ cắt parabol $y = x^{2}$ tại hai điểm. Tọa độ của các giao điểm là:

A, (1; 1) và (-3;9)

B. (1;1) và (3;9)

C. (-1; 1) và (3;9)

D. (-1;1) và ( -3;9)

Xem đáp án

Chọn đáp án C

Câu 16:

Cho hàm số $y = f (x) = (1 + m^{4}) x + 1, m$ là tham số. Khẳng định nào sau đây đúng

A. $f (1) > f (2)$

B. $f (4) < f (2)$

C. $f (2) < f (3)$

D. $f (- 1) > f (0)$

Xem đáp án

Chọn đáp án C

Câu 17:

Hệ phương trình $\{\begin{cases} x + y = 3 \\ m x - y = 3 \end{cases}$ có nghiệm $(x_{0}; y_{0})$ thỏa mãn b $x_{0} = 2 y_{0} .$ Khi đó giá trị của m là

A. m= 3

B. m=2

C. m= 5

D. m=4

Xem đáp án

Chọn đáp án B

Câu 18:

Tìm tham số m để phương trình $x^{2} + x + m + 1 = 0$ có hai nghiệm $x_{1}, x_{2}$ thỏa mãn $x_{1}^{2} + x_{2}^{2} = 5.$

A. m= -3

B. m=1

C. m=2

D. m=0

Xem đáp án

Chọn đáp án A

Câu 19:

Cho tam giác ABC vuông tại A, có $A C = 20 c m .$ Đường tròn đường kính AB cắt BC tại M(M không trùng với B), tiếp tuyến tại M của đường tròn đường kính AB cắt AC tai I. Độ dài đoạn AI bằng:

A. 6cm

B. 9cm

C. 10cm

D. 12cm

Xem đáp án

Chọn đáp án C

Câu 20:

Cho đường tròn $(O; R)$ và dây cung AB thỏa mãn $\hat{A O B} = 90^{0} .$ Độ dài cung nhỏ $\overset{⏜}{A B}$ bằng:

A. $\frac{π R}{2}$

B. $π R$

C. $\frac{π R}{4}$

D. $\frac{3 π R}{2}$

Xem đáp án

Chọn đáp án A

Câu 21:

a, Giải hệ phương trình

\{\begin{cases} x - y = 2 \\ 3 x + 2 y = 11 \end{cases}

Xem đáp án

a) Ta có : $\{\begin{cases} x - y = 2 \\ 3 x + 2 y = 11 \end{cases} \Leftrightarrow \{\begin{cases} 2 x - 2 y = 4 \\ 3 x + 2 y = 11 \end{cases} \Leftrightarrow \{\begin{cases} 5 x = 15 \\ x - y = 2 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = 1 \end{cases}$

Vậy hệ có nghiệm $(x; y) = (3; 1)$

Câu 22:

b, Rút gọn biểu thức $A = [\frac{2 (x - 2 \sqrt{x} + 1)}{x - 4} - \frac{2 \sqrt{x} - 1}{\sqrt{x} + 2}] : \frac{\sqrt{x}}{\sqrt{x} - 2}$ với $x > 0; x \neq 4$

Xem đáp án

$\begin{array}{l} b) [\frac{2 (x - 2 \sqrt{x} + 1)}{x - 4} - \frac{2 \sqrt{x} - 1}{\sqrt{x} + 2}] : \frac{\sqrt{x}}{\sqrt{x} - 2} (x > 0, x \neq 4) \\ = [\frac{2 (x - 2 \sqrt{x} + 1)}{(\sqrt{x} - 2) (\sqrt{x} + 2)} - \frac{(2 \sqrt{x} - 1) (\sqrt{x} - 2)}{(\sqrt{x} + 2) (\sqrt{x} - 2)}] : \frac{\sqrt{x}}{\sqrt{x} - 2} \\ = \frac{2 x - 4 \sqrt{x} + 2 - 2 x + \sqrt{x} + 4 \sqrt{x} - 2}{(\sqrt{x} + 2) (\sqrt{x} - 2)} . \frac{\sqrt{x} - 2}{\sqrt{x}} = \frac{\sqrt{x}}{(\sqrt{x} + 2) (\sqrt{x} - 2)} . \frac{\sqrt{x} - 2}{\sqrt{x}} = \frac{1}{\sqrt{x} + 2} \end{array}$

Vậy $A = \frac{1}{\sqrt{x} + 2}$

Câu 23:

Cho phương trình $x^{2} - (m + 1) x + m - 4 = 0 (1), m$ là tham số

a) Giải phương trình (1) khi m= 1

Xem đáp án

a) Khi m=1 thì (1) trở thành $x^{2} - (1 + 1) x + 1 - 4 = 0 \Leftrightarrow x^{2} - 2 x - 3 = 0 \Leftrightarrow [\begin{array}{l} x = - 1 \\ x = 3 \end{array}$

Vậy với m =1 thì phương trình có tập nghiệm $S = \{- 1; 3\}$

Câu 24:

b, Tìm giá trị của m để phương trình (1) có hai nghiệm $x_{1}, x_{2}$ thỏa mãn:

$(x_{1}^{2} - m x_{1} + m) (x_{2}^{2} - m x_{2} + m) = 2$

Xem đáp án

a) Phương trình có hai nghiệm $\Leftrightarrow \{\begin{cases} a = 1 \neq 0 \\ Δ = {(m + 1)}^{2} - 4 (m - 4) \geq 0 \end{cases}$

$\Leftrightarrow m^{2} + 2 m + 1 - 4 m + 16 \geq 0 \Leftrightarrow m^{2} - 2 m + 17 \geq 0$ (luôn đúng do $m^{2} - 2 m + 17 > 0)$

Do đó phương trình (1) luôn có hai nghiệm phân biệt $x_{1}, x_{2}$

Ta có: $x^{2} - (m + 1) x + m - 4 = 0 \Leftrightarrow x^{2} - m x - x + m - 4 = 0 \Leftrightarrow x^{2} - m x + m = x + 4$

Do $x_{1}, x_{2}$ là nghiệm của (1) nên $\{\begin{cases} x_{1}^{2} - m x_{1} + m = x_{1} + 4 \\ x_{2}^{2} - m x_{2} + m = x_{2} + 4 \end{cases}$

Thay vào đẳng thức bài ta được : $(x_{1} + 4) (x_{2} + 4) = 2$

$\Leftrightarrow x_{1} x_{2} + 4 (x_{1} + x_{2}) + 16 = 2 \Leftrightarrow x_{1} x_{2} + 4 (x_{1} + x_{2}) + 14 = 0 (2)$

Theo định lý Vi et ta có: $\{\begin{cases} x_{1} + x_{2} = m + 1 \\ x_{1} x_{2} = m - 4 \end{cases},$ thay vào (2) ta được:

$m - 4 + 4 (m + 1) + 14 = 0 \Leftrightarrow 5 m + 14 = 0 \Leftrightarrow m = - \frac{14}{5}$

Vậy $m = - \frac{14}{5}$ là giá trị cần tìm .

Câu 25:

Đầu năm học, Hội Khuyến học của một tỉnh tặng cho trường A tổng số 245 quyển sách gồm sách Toán và sách Ngữ văn. Nhà trường đã dùng $\frac{1}{2}$ số sách Toán và $\frac{2}{3}$ số sách Ngữ văn để phát cho các bạn học sinh có hoàn cảnh khó khăn. Biết rằng mỗi bạn nhận được một quyển sách Toán và một quyển sách Ngữ văn. Hỏi Hội khuyến học tỉnh đã tặng cho trường A mỗi loại sách bao nhiêu quyển ?

Xem đáp án

Gọi số sách Toán Hội khuyến học tính tặng cho trường A là x quyển ( $0 < x < 245, x \in ℕ)$

Thì số sách Ngữ văn hội khuyến học tính tặng cho trường A là $245 - x$ (quyển)

Số sách toán nhà trường dùng để phát cho học sinh khó khăn là $\frac{1}{2} x$ quyển

Số sách Ngữ văn nhà trường dùng để phát cho học sinh khó khăn là $\frac{2}{3} (245 - x)$ quyển

Vì mỗi bạn nhận được 1 quyển sách Toán và 1 quyển sách Ngữ văn nên số quyển sách Toán và số quyển sách Ngữ văn đem phát là bằng nhau.

Ta có phương trình : $\frac{1}{2} x = \frac{2}{3} (245 - x)$

$\begin{array}{l} \Leftrightarrow \frac{1}{2} x = \frac{490}{3} - \frac{2 x}{3} \Leftrightarrow \frac{7}{6} x = \frac{490}{3} \\ \Leftrightarrow x = \frac{490}{3} : \frac{7}{6} \Leftrightarrow x = 140 (t m) \end{array}$

Vậy số sách Toán Hội khuyến học tỉnh tặng cho trường A là 140 quyển

Số sách Ngữ văn Hội khuyến học tỉnh tặng cho trường A là $245 - 140 = 105$ quyển

Câu 26:

Cho tam giác ABC nội tiếp đường tròn (O) đường kính AC ( $B A < B C)$ .

Trên đoạn thẳng OC lấy điểm I bất kỳ $(I \neq C)$ . Đường thẳng BI cắt đường tròn (O) tại điểm thứ hai là D. Kẻ $C H ⊥ B D (H \in B D),$ DK vuông góc với AC ( $K \in A C)$

a,Chứng minh rằng tứ giác DHKC là tứ giác nội tiếp

Xem đáp án

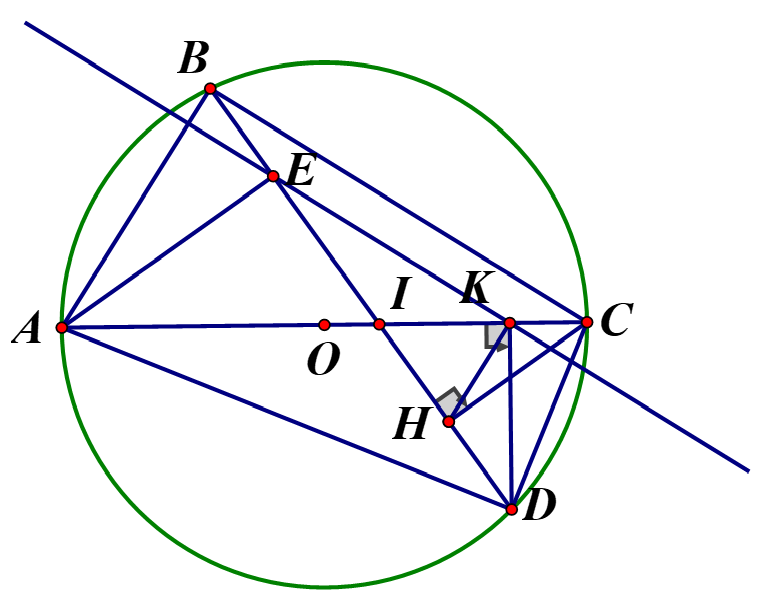
Cho tam giác ABC nội tiếp đường tròn (O) đường kính AC (ảnh 1)

a) Xét tứ giác DHKC có: $\hat{D H C} = 90^{0} ($ do $C H ⊥ B D), \hat{D K C} = 90^{0}$ (do $D K ⊥ A C)$

Suy ra $\hat{D H C} = \hat{D K C} (= 90^{0})$ nên hai đỉnh H, K kề nhau cùng nhìn cạnh CD dưới các góc vuông nên tứ giác $D H C K$ là tứ giác nội tiếp

Câu 27:

b, Cho độ dài đoạn thẳng AC là 4cm và $\hat{A B D} = 60^{0} .$ Tính diện tích tam giác ACD.

Xem đáp án

b) Gọi O là trung điểm AC

Xét đường tròn (O) có $\hat{A B D} = 60^{0} \Rightarrow \hat{A C D} = \hat{A B D} = 60^{0}$ (hai góc nôi tiếp cùng chắn cung AD)

Lại có $\hat{C D A} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn )

Xét tam giác $A C D$ vuông tại D có $A C = 4 c m, \hat{A C D} = 60^{0}$ nên

$A D = A C . \sin \hat{A C D} = 4. \sin 60^{0} = 2 \sqrt{3} (c m)$

Và CD $= A C . \cos \hat{A C D} = 4. \cos 60^{0} = 2 c m$

Diện tích tam giác ACD là $S_{A C D} = \frac{1}{2} A D . D C = \frac{1}{2} .2 \sqrt{3} .2 = 2 \sqrt{3} c m^{2}$

Câu 28:

c, Đường thẳng đi qua K song song với BC cắt đường thẳng BD tại E. Chứng minh rằng khi I thay đổi trên đoạn thẳng $O C (I \neq C)$ thì điểm E luôn thuộc một đường tròn cố định

Xem đáp án

c, Vì $E K / / B C \Rightarrow \hat{D E K} = \hat{D B C} (1)$ (hai góc ở vị trí đồng vị)

Xét đường tròn (O) có $\hat{D B C} = \hat{D A C} (2)$ (hai góc nội tiếp cùng chắn cung CD)

Từ (1) và (2) suy ra $\hat{D E K} = \hat{D A K}$

Suy ra tứ giác AEKD có hai đỉnh A, E cùng nhìn cạnh KD dưới các góc bằng nhau nên tứ giác AEKD là tứ giác nội tiếp , suy ra $\hat{A E D} = \hat{A K D} = 90^{0}$

Do đó $A E ⊥ E B$ suy ra $Δ A E B$ vuông tại E

Lại có AB cố định nên E thuộc đường tròn đường kính AB cố định khi I thay đổi trên đoạn OC

Câu 29:

Cho x, y là các số thực thỏa mãn điều kiện $x^{2} + y^{2} = 1.$ Tìm giá trị nhỏ nhất của biểu thức $P = (3 - x) (3 - y)$

Xem đáp án

Áp dụng bất đẳng thức Bu-nhi-a cốp xki ta có:

${(x + y)}^{2} \leq (1^{2} + 1^{2}) (x^{2} + y^{2}) = 2 \Rightarrow x + y \leq \sqrt{2}$

Lại có: $P = (3 - x) (3 - y) = 9 - 3 (x + y) + x y = 9 - 3 (x + y) + \frac{{(x + y)}^{2} - (x^{2} + y^{2})}{2}$

$\begin{array}{l} = 9 - 3 (x + y) + \frac{{(x + y)}^{2} - 1}{2} = \frac{{(x + y)}^{2} - 6 (x + y) + 17}{2} = \frac{[{(x + y)}^{2} - 6 (x + y) + 9] + 8}{2} \\ = \frac{1}{2} {(x + y - 3)}^{2} + 4 \end{array}$

Vì $x + y \leq \sqrt{2}$ nên

$\begin{array}{l} x + y - 3 \leq \sqrt{2} - 3 < 0 \Rightarrow {(x + y - 3)}^{2} \geq {(\sqrt{2} - 3)}^{2} = 11 - 6 \sqrt{2} \\ \Rightarrow P = \frac{1}{2} {(x + y - 3)}^{2} + 4 \geq \frac{11 - 6 \sqrt{2}}{2} = \frac{19}{2} - 3 \sqrt{2} \\ \Rightarrow P \geq \frac{19}{2} - 3 \sqrt{2} \end{array}$

Dấu $" = "$ xảy ra khi $x = y = \frac{\sqrt{2}}{2}$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 3

Danh sách câu hỏi

Bài thi liên quan