12 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 24

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 24

3330 lượt thi
12 câu hỏi
45 phút

Danh sách câu hỏi

Câu 1:

Cho hai biểu thức $A = \frac{4 (\sqrt{x} + 1)}{25 - x}$ và $B = (\frac{15 - \sqrt{x}}{x - 25} + \frac{2}{\sqrt{x} + 5}) : \frac{\sqrt{x} + 1}{\sqrt{x} - 5}$ ( $x \geq 0, x \neq 25)$

a, Tính giá trị của biểu thức A khi x=9

Xem đáp án

a, Khi $x = 9 (t m)$ thay vào A ta được $A = \frac{4. (\sqrt{9} + 1)}{25 - 9} = \frac{16}{16} = 1$

Vậy với x=9 thì A= 1

Câu 2:

b,Rút gọn biểu thức B

Xem đáp án

b, Điều kiện $x \geq 0, x \neq 25$

$\begin{array}{l} B = (\frac{15 - \sqrt{x}}{x - 25} + \frac{2}{\sqrt{x} + 5}) \frac{\sqrt{x} + 1}{\sqrt{x} - 5} = [\frac{15 - \sqrt{x}}{(\sqrt{x} - 5) (\sqrt{x} + 5)} + \frac{2}{\sqrt{x} + 5}] . \frac{\sqrt{x} - 5}{\sqrt{x} + 1} \\ = \frac{15 - \sqrt{x} + 2 (\sqrt{x} - 5)}{(\sqrt{x} - 5) (\sqrt{x} + 5)} . \frac{\sqrt{x} - 5}{\sqrt{x} + 1} = \frac{15 - \sqrt{x} + 2 \sqrt{x} - 10}{(\sqrt{x} + 5) (\sqrt{x} + 1)} \\ = \frac{\sqrt{x} + 5}{(\sqrt{x} + 5) (\sqrt{x} + 1)} = \frac{1}{\sqrt{x} + 1} \end{array}$

Câu 3:

c,Tìm tất cả các giá trị nguyên của x để biểu thức P = AB đạt giá trị nguyên lớn nhất

Xem đáp án

c, Điều kiện $x \geq 0, x \neq 25$

Ta có: $P = A B = \frac{4 (\sqrt{x} + 1)}{25 - x} . \frac{1}{\sqrt{x} + 1} = \frac{4}{25 - x}$

$x \in ℤ \Rightarrow P \in ℤ \Leftrightarrow \frac{4}{25 - x} \in ℤ \Rightarrow 4 ⋮ (25 - x) \Rightarrow (25 - x) \in U (4)$

Mà Ư(4)= $\{\pm 1; \pm 2; \pm 4\} \Rightarrow (25 - x) \in \{\pm 1; \pm 2; \pm 4\}$

Ta có bảng giá trị

$25 - x$	-4	-2	-1	1	2	4
x	29 ™	27™	26™	24 ™	23 ™	1™
P	-1	-2	-4	4	2	1

$\Rightarrow x \in \{23; 24; 26; 27; 29\}$ thì $P \in ℤ$

Qua bảng giá trị ta thấy với x= 24 thì P=4 là số nguyên lớn nhất

Vậy x= 24 thỏa mãn điều kiện bài toán.

Câu 4:

a,Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình

Hai đội công nhân cùng làm chung một công việc thì sau ngày 15 làm xong. Nếu đôi thứ nhất làm riêng trong 3 ngày rồi dừng và đội thứ hai làm tiếp công việc đó trong 5 ngày thì cả hai đội hoàn thành được 20% công việc. Hỏi nếu mỗi đội làm riêng thì trong bao nhiêu ngày mới xong công việc trên ?

Xem đáp án

a, Gọi số ngày làm một mình xong công việc của đội 1 là x (ngày) $(x > 15)$

Số ngày làm một mình xong công việc của đội 2 là y (ngày ) ( $y > 15)$

Trong một ngày đội 1 làm được số phần công việc là $\frac{1}{x}$ (công việc)

Trong một ngày đội 2 làm được số phần công việc là $\frac{1}{y}$ (công việc)

Vì hai đội làm chung trong 15 ngày thì xong nên ta có phương trình: $\frac{15}{x} + \frac{15}{y} = 1 (1)$

Trong 3 ngày đội 1 làm được $\frac{3}{x}$ công việc, trong 5 ngày đội 2 làm được $\frac{5}{y}$ công việc

Đội 1 làm trong 3 này và đội hai làm trong 5 ngày được $25 % = \frac{1}{4}$ công việc nên ta có phương trình $\frac{3}{x} + \frac{5}{y} = \frac{1}{4} (2)$

Từ (1) và (2) ta có hệ phương trình: $\{\begin{cases} \frac{15}{x} + \frac{15}{y} = 1 \\ \frac{3}{x} + \frac{5}{y} = \frac{1}{4} \end{cases}$

Đặt $\{\begin{cases} \frac{1}{x} = a \\ \frac{1}{y} = b \end{cases}$ ta được: $\{\begin{cases} 15 a + 15 b = 1 \\ 3 a + 5 b = \frac{1}{4} \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{1}{24} \\ b = \frac{1}{40} \end{cases} \Rightarrow \{\begin{cases} \frac{1}{x} = \frac{1}{24} \\ \frac{1}{y} = \frac{1}{40} \end{cases} \Leftrightarrow \{\begin{cases} x = 24 (t m) \\ y = 40 (t m) \end{cases}$

Vậy đội 1 mất 24 ngày làm xong, đội 2 mất 40 ngày làm xong

Câu 5:

b, Một bồn nước inox có dạng một hình trụ với chiều cao 1,75m và diện tích đáy là $0,32 m^{2} .$ Hỏi bồn nước này đựng đầy nước được bao nhiêu mét khối (Bỏ qua bề dày của bồn nước)

Xem đáp án

b,Thể tích bồn nước là: $V = S h = 0,32.1,75 = 0,56 (m^{3})$

Vậy bồn nước đựng được $0,56 m^{3}$ nước

Câu 6:

Giải phương trình:

x^{4} - 7 x^{2} - 18 = 0

(1)

Xem đáp án

Đặt $x^{2} = t (t \geq 0)$ ta có phương trình : $t^{2} - 7 t - 18 = 0$

$\begin{array}{l} \Leftrightarrow t^{2} - 9 t + 2 t - 18 = 0 \\ \Leftrightarrow t (t - 9) + 2 (t - 9) = 0 \\ \Leftrightarrow (t + 2) (t - 9) = 0 \\ \Leftrightarrow [\begin{array}{l} t = - 2 (k t m) \\ t = 9 (t m) \Rightarrow x^{2} = 9 \Leftrightarrow [\begin{array}{l} x = 3 \\ x = - 3 \end{array} \end{array} \end{array}$

Vậy $S = \{\pm 3\}$

Câu 7:

Trong mặt phẳng tọa độ Oxy cho đường thẳng $(d) : y = 2 m x - m^{2} + 1$ và parabol $(P) : y = x^{2}$

a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt

Xem đáp án

a, Xét phương trình hoành độ giao điểm của (P) và (d) ta có:

$x^{2} = 2 m x - m^{2} + 1 \Leftrightarrow x^{2} - 2 m x + m^{2} - 1 = 0 (*)$

Số giao điểm của (d) và (P) cũng chính là số nghiệm của phương trình (*)

Phương trình (*) có $Δ' = m^{2} - (m^{2} - 1) = 1 > 0$ nên (d) luôn cắt (P) tại hai điểm phân biệt

Câu 8:

b,Tìm tất cả các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có hoành độ $x_{1}, x_{2}$ thỏa mãn $\frac{1}{x_{1}} + \frac{1}{x_{2}} = \frac{- 2}{x_{1} x_{2}} + 1$

Xem đáp án

Theo hệ thức Viet ta có: $\{\begin{cases} x_{1} + x_{2} = 2 m \\ x_{1} x_{2} = m^{2} - 1 \end{cases}$

Xét $\frac{1}{x_{1}} + \frac{1}{x_{2}} = \frac{- 2}{x_{1} x_{2}} + 1 (x_{1} x_{2} \neq 0 \Leftrightarrow m^{2} - 1 \neq 0 \Leftrightarrow m \neq \pm 1)$

$\begin{array}{l} \Leftrightarrow \frac{x_{1} + x_{2}}{x_{1} x_{2}} = \frac{- 2 + x_{1} x_{2}}{x_{1} x_{2}} \\ \Rightarrow x_{1} + x_{2} - x_{1} x_{2} + 2 = 0 \\ \Leftrightarrow 2 m - m^{2} + 1 + 2 = 0 \\ \Leftrightarrow m^{2} - 2 m - 3 = 0 \\ \Leftrightarrow [\begin{array}{l} m = - 1 (k t m) \\ m = 3 (t m) \end{array} \end{array}$

Vậy m=3 là giá trị thỏa mãn đề bài

Câu 9:

Cho tam giác ABC có ba góc nhọn AB< AC nội tiếp đường tròn (O). Hai đường cao BE và CF của tam giác ABC cắt nhau tại H

a, Chứng minh bốn điểm B, C, E, F cùng thuộc một đường tròn

Xem đáp án

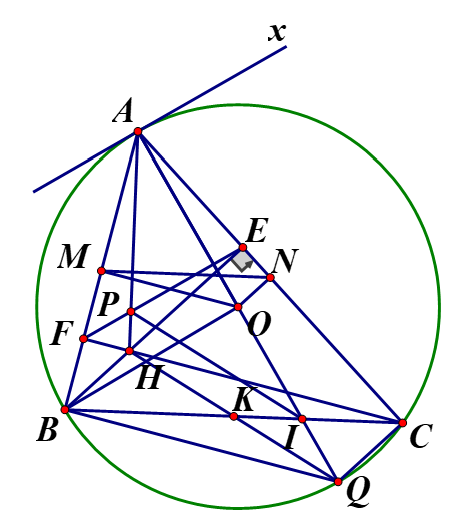
Cho tam giác ABC có ba góc nhọn AB< AC nội tiếp đường tròn (O (ảnh 1)

Ta có $\hat{B E C} = \hat{B F C} = 90^{0} (g t) \Rightarrow$ Tứ giác BFEC là tứ giác nội tiếp (tứ giác có 2 đỉnh kề nhau cùng nhìn một cạnh dưới các góc bằng nhau).

Vậy bốn điểm B, C, E,F cùng thuộc một đường tròn.

Câu 10:

b,Chứng minh đường thẳng OA vuông góc với đường thẳng EF

Xem đáp án

b,Kẻ tiếp tuyến Ax của đường tròn (O) tại A, ta có $A x ⊥ O A$

Ta có: $\hat{x A E} = \hat{A B C}$ (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn $\overset{⏜}{A C})$

Mà $\hat{A B C} = \hat{A E F}$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nôi tiếp)

$\Rightarrow \hat{x A E} = \hat{A E F}$ , mà hai góc này ở vị trí so le trong $\Rightarrow E F / / A x \Rightarrow E F ⊥ O A$

Câu 11:

c, Gọi K là trung điểm của đoạn thẳng BC Đường thẳng AO cắt đường thẳng BC tại điểm I, đường thẳng EF cắt đường thẳng AH tại điểm P. Chứng minh tam giác APE đồng dạng với tam giác AIB và đường thẳng KH song song với đường thẳng IP

Xem đáp án

c,Ta đã chứng minh được $\hat{D A F} = \hat{G A N}$ hay $\hat{I A B} = \hat{P A E}$

Lại có: $\hat{A E F} = \hat{A B C}$ (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp)

$\Rightarrow Δ A P E ~ Δ A I B (g . g)$

Kéo dài AI cắt (O) tại Q $\Rightarrow A Q$ là đường kính của (O)

Nối $B Q, C Q$ ta có: $\hat{A B Q} = 90^{0}$ (góc nội tiếp chắn nửa đường tròn) $\Rightarrow A B ⊥ B Q$

Mà $C H ⊥ A B \Rightarrow C H / / B Q$

Hoàn toàn tương tự ta chứng minh được: $B H / / C Q$

Suy ra BHCQ là hình bình hành mà K là trung điểm của BC (gt)

$\Rightarrow K$ cũng là trung điểm của HQ nên $H, K, Q$ thẳng hàng

Ta có: $Δ A P E ~ Δ A I B (c m t) \Rightarrow \frac{A P}{A I} = \frac{A E}{A B} (3)$

Xét $Δ A H E$ và $Δ A Q B$ có:

$\begin{array}{l} \hat{A E H} = \hat{A B Q} = 90^{0}; \hat{Q A B} = \hat{E A H} (c m t) (d o .. \hat{D A F} = \hat{G A N}) \\ \Rightarrow Δ A H E ~ Δ A Q B (g . g) \Rightarrow \frac{A H}{A Q} = \frac{A E}{A B} (4) \end{array}$

Từ (3) và (4) $\Rightarrow \frac{A P}{A I} = \frac{A H}{A Q} \Rightarrow \frac{A P}{A H} = \frac{A I}{A Q} \Rightarrow P I / / H Q$ (định lý Talet đảo) (đpcm)

Câu 12:

Cho biểu thức $P = a^{4} + b^{4} - a b$ , với $a, b$ là các số thực thỏa mãn $a^{2} + b^{2} + a b = 3.$ Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P

Xem đáp án

Ta có: $a^{2} + b^{2} + a b = 3 \Leftrightarrow a^{2} + b^{2} = 3 - a b$

Ta thấy ${(a - b)}^{2} \geq 0 \Leftrightarrow a^{2} + b^{2} \geq 2 a b \Leftrightarrow 3 - a b \geq 2 a b \Leftrightarrow a b \leq 1$

Lại có: ${(a + b)}^{2} \geq 0 \Leftrightarrow a^{2} + b^{2} \geq - 2 a b \Leftrightarrow 3 - a b \geq - 2 a b \Leftrightarrow 3 \geq - a b \Leftrightarrow a b \geq - 3$

$\Rightarrow - 3 \leq a b \leq 1$

Xét $a^{2} + b^{2} = 3 - a b$ với $- 3 \leq a b \leq 1$

$\begin{array}{l} \Leftrightarrow {(a^{2} + b^{2})}^{2} = {(3 - a b)}^{2} \\ \Leftrightarrow a^{4} + b^{4} + 2 a^{2} b^{2} = 9 - 6 a b + a^{2} b^{2} \\ \Leftrightarrow a^{4} + b^{4} = - a^{2} b^{2} - 6 a b + 9 \end{array}$

Khi đó: $P = a^{4} + b^{4} - a b = - a^{2} b^{2} - 6 a b + 9 - a b = - {(a b)}^{2} - 7 a b + 9 = \frac{85}{4} - {(a b + \frac{7}{2})}^{2}$

Vì $- 3 \leq a b \leq 1 \Rightarrow \frac{1}{2} \leq a b + \frac{7}{2} \leq \frac{9}{2} \Leftrightarrow {(a b + \frac{7}{2})}^{2} \leq \frac{81}{4}$

Suy ra $P = \frac{85}{4} - {(a b + \frac{7}{2})}^{2} \geq \frac{85}{4} - \frac{81}{4} = 1 \Leftrightarrow P \geq 1$

Dấu $" = "$ xảy ra khi $a b = 1$ và $a^{2} + b^{2} = 2 \Rightarrow [\begin{array}{l} a = 1, b = 1 \\ a = - 1, b = - 1 \end{array}$

Ta lại có: $P = - {(a b)}^{2} - 7 a b + 9 = (a b + 3) (- a b - 4) + 21$

Mà $- 3 \leq a b \leq 1$ nên $\{\begin{cases} a b + 3 \geq 0 \\ - a b - 4 < 0 \end{cases}$ nên $(a b + 3) (- a b - 4) + 21$

Dấu $" = "$ xảy ra khi $\{\begin{cases} a b = - 3 \\ a^{2} + b^{2} + a b = 3 \end{cases} \Leftrightarrow \{\begin{cases} a b = - 3 \\ {(a + b)}^{2} = 0 \end{cases} \Leftrightarrow [\begin{array}{l} \{\begin{cases} a = \sqrt{3} \\ b = - \sqrt{3} \end{cases} \\ \{\begin{cases} a = - \sqrt{3} \\ b = \sqrt{3} \end{cases} \end{array}$

Vậy giá trị lớn nhất của P là 21, giá trị nhỏ nhất của P là 1.

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 24

Danh sách câu hỏi

Bài thi liên quan