14 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 6

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 6

3344 lượt thi
14 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Khi $x = 7$ biểu thức $\frac{4}{\sqrt{x + 2} - 1}$ có giá trị là:

A. $\frac{1}{2}$

B. $\frac{4}{\sqrt{8}}$

C. $\frac{4}{3}$

D. 2

Xem đáp án

Chọn đáp án D

Câu 2:

Trong các hàm số sau, hàm số nào đồng biến trên R ?

A. $y = 1 - x$

B. $y = 2 x - 3$

C. $y = (1 - \sqrt{2}) x$

D. $y = - 2 x + 6$

Xem đáp án

Chọn đáp án B

Câu 3:

Số nghiệm của phương trình $x^{4} - 3 x^{2} + 2 = 0$ là:

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Chọn đáp án D

Câu 4:

Cho hàm số $y = a x^{2}$ $(a \neq 0)$ . Điểm $M (1; 2)$ thuộc đồ thị hàm số khi

A. $a = 2$

B. $a = \frac{1}{2}$

C. $a = - 2$

D. $a = \frac{1}{4}$

Xem đáp án

Chọn đáp án A

Câu 5:

Từ điểm A nằm bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB,AC tới dường tròn B,C là các tiếp điểm). Kẻ đường kính BK. Biết $\hat{B A C} = 30^{0} .$ Số đo của cung nhỏ CK là:

A. $30^{0}$

B. $60^{0}$

C. $120^{0}$

D. $150^{0}$

Xem đáp án

Chọn đáp án A

Câu 6:

Cho tam giác ABC vuông tại A. Gọi H là chân đường cao hạ từ đỉnh A xuống cạnh BC, Biết $A H = \sqrt{12} c m, \frac{H B}{H C} = \frac{1}{3} .$ Đọ dài đoạn BC là:

A. 6cm

B. 8cm

C. $4 \sqrt{3} c m$

D. 12cm

Xem đáp án

Chọn đáp án B

Câu 7:

Cho biểu thức $A = \frac{{(\sqrt{x} + 1)}^{2} + {(\sqrt{x} - 1)}^{2}}{(\sqrt{x} - 1) (\sqrt{x} + 1)} - \frac{3 \sqrt{x} + 1}{x - 1}$ với $x \geq 0, x \neq 1$

a) Rút gọn biểu thức A

Xem đáp án

a) Rút gọn biểu thức

Điều kiện : $x \geq 0, x \neq 1$

$\begin{array}{l} A = \frac{{(\sqrt{x} + 1)}^{2} + {(\sqrt{x} - 1)}^{2}}{(\sqrt{x} - 1) (\sqrt{x} + 1)} - \frac{3 \sqrt{x} + 1}{x - 1} \\ = \frac{x + 2 \sqrt{x} + 1 + x - 2 \sqrt{x} + 1}{x - 1} - \frac{3 \sqrt{x} + 1}{x - 1} \\ = \frac{2 x + 2}{x - 1} - \frac{3 \sqrt{x} + 1}{x - 1} = \frac{2 x - 2 \sqrt{x} - \sqrt{x} + 1}{x - 1} \\ = \frac{2 \sqrt{x} (\sqrt{x} - 1) - (\sqrt{x} - 1)}{(\sqrt{x} + 1) (\sqrt{x} - 1)} = \frac{(2 \sqrt{x} - 1) (\sqrt{x} - 1)}{(\sqrt{x} + 1) (\sqrt{x} - 1)} \\ = \frac{2 \sqrt{x} - 1}{\sqrt{x} + 1} \end{array}$

Câu 8:

b, Tìm x là số chính phương để 2019A là số nguyên.

Xem đáp án

a) Điều kiện: $x \geq 0, x \neq 1$

Ta có: $2019 A = 2019. \frac{2 \sqrt{x} - 1}{\sqrt{x} + 1} = 2019. (2 - \frac{3}{\sqrt{x} + 1}) = 4038 - \frac{6057}{\sqrt{x} + 1}$

Vì $2019 A \in ℤ \Rightarrow \sqrt{x} + 1 \in U (6057)$

Mà $\sqrt{x} + 1 \geq 1 \forall x \geq 0, x \neq 1 \Rightarrow \sqrt{x} + 1 \in \{1; 3; 9; 2019; 6057\}$

TH1: $\sqrt{x} + 1 = 1 \Leftrightarrow x = 0 (t m)$

TH2: $\sqrt{x} + 1 = 3 \Leftrightarrow \sqrt{x} = 2 \Leftrightarrow x = 4 (t m)$

TH3: $\sqrt{x} + 1 = 9 \Leftrightarrow \sqrt{x} = 8 \Leftrightarrow x = 64 (t m)$

TH4: $\sqrt{x} + 1 = 2019 \Leftrightarrow \sqrt{x} = 2018 \Leftrightarrow x = 2018^{2} (t m)$

TH5: $\sqrt{x} + 1 = 6057 \Leftrightarrow \sqrt{x} = 6056 \Leftrightarrow x = 6056^{2} (t m)$

Vậy $x \in \{0; 4; 64; 2018^{2}; 6056^{2}\}$

Câu 9:

An đếm số bài kiểm tra một tiết đạt điểm 9 và điểm 10 của mình thấy nhiều hơn 16 bài. Tổng số điểm của tất cả các bài kiểm tra đạt điểm 9 và điểm 10 đó là 160. Hỏi An được bao nhiêu bài đạt điểm 9 và bao nhiêu bài điểm 10

Xem đáp án

Gọi số bài kiểm tra 1 tiết đạt điểm 9 là x (bài ) $(x \in ℕ)$ và số bài kiểm tra 1 tiết đạt điểm 10 là y (bài)

$(y \in ℕ)$

Do số bài kiểm tra 1 tiết đạt điểm 9 và điểm 10 nhiều hơn 16 bài nên $x + y > 16 \Leftrightarrow 9 x + 9 y > 144 (1)$

Tổng số điểm của x bài kiểm tra 1 tiết đạt điểm 9 là 9x (điểm)

Tổng số điểm của y bài kiểm tra 1 tiết đạt điểm 10 là 10y (điểm)

Do tổng số điểm của tất cả các bài kiểm tra đạt 9 điểm và 10 điểm là 160 nên ta có phương trình:

$9 x + 10 y = 160 \Leftrightarrow 9 x = 160 - 10 y$

Thay vào (1) ta có: $160 - 10 y + 9 y > 144 \Leftrightarrow y < 16$

Do $y \in ℕ \Rightarrow y \in \{0; 1; 2; 3; .......; 15\}$

Ta có:

$x \in ℕ \Rightarrow 9 x = 160 - 10 y \equiv 0 (\mod 9) \Rightarrow 153 + 7 - 9 y - y \equiv 0 (\mod 9)$

$\begin{array}{l} \Leftrightarrow 7 - y \equiv 0 (\mod 9) \Leftrightarrow y \equiv 7 (\mod 9) \\ \Rightarrow y = 7 \Rightarrow x = 10 (t m) \end{array}$

Vậy số bài kiểm tra 1 tiết đạt điểm 9 là 10 bài và số bài kiểm tra 1 tiết đạt điểm 10 là 7 bài

Câu 10:

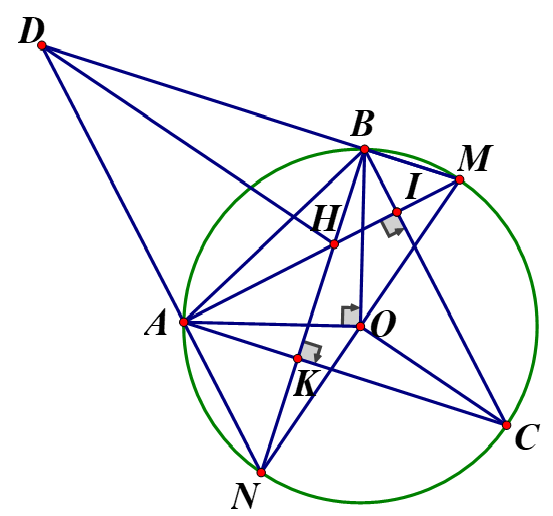
Cho đường tròn (O), hai điểm A, B nằm trên (O) sao cho $\hat{A O B} = 90^{0} .$ Điểm C nằm trên cung lớn AB sao cho $A C > B C$ và tam giác ABC có ba góc đều nhọn. Các đường cao $A I, B K$ của tam giác ABC cắt nhau tại H. BK cắt (O) tại điểm N (N khác điểm B); AI cắt (O) tại điểm M (khác điểm A), NA cắt MB tại điểm D. Chứng minh rằng

a) Tứ giác CIHK nội tiếp một đường tròn

Xem đáp án

Cho đường tròn (O), hai điểm A, B nằm trên (O) sao cho góc AOB = 90 độ (ảnh 1)

Ta có $A I ⊥ B C \Rightarrow \hat{C I H} = 90^{0}, B K ⊥ A C \Rightarrow \hat{C K H} = 90^{0}$

Xét tứ giác CIFK có $\hat{C I H} + \hat{C K H} = 90^{0} + 90^{0} = 180^{0} \Rightarrow$ Tứ giác CIFK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng $180^{0})$

Câu 11:

b, MN là đường kính của đường tròn (O)

Xem đáp án

Ta có : $\hat{A C B} = \hat{A M B} = \frac{1}{2} \hat{A O B} = \frac{1}{2} {.90}^{0} = 45^{0}$ (góc nội tiếp và góc ở tâm cùng chắn cung AB)

Có $A I ⊥ B C \Rightarrow Δ I A C$ vuông tại I , lại có : $\hat{A C B} = \hat{A C I} = 45^{0} \Rightarrow Δ I A C$ vuông cân tại I

$\Rightarrow \hat{I A C} = 45^{0}$ $\Rightarrow \hat{A M B} = \hat{I A C} = 45^{0}$ , mà hai góc này ở vi trí so le trong $\Rightarrow B M / / A C$

Mà $B K ⊥ A C (g t)$ hay $B N ⊥ A C \Rightarrow B M ⊥ B N$ (từ vuông góc đến song song)

$\Rightarrow \hat{M B N} = 90^{0} \Rightarrow \hat{M B N}$ nội tiếp chắn nửa đường tròn $\Rightarrow M N$ là đường kính của đường tròn (O).

Câu 12:

c, OC song song với DH

Xem đáp án

Có $\hat{I A C} = 45^{0} (c m t) \Rightarrow \hat{M A C} = 45^{0}$

Mà $\hat{M A C} = \frac{1}{2} \hat{M O C}$ (góc nội tiếp và góc ở tâm cùng chắn cung MC)

$\Rightarrow \hat{M O C} = 2 \hat{M A C} = {2.45}^{0} = 90^{0} \Rightarrow O C ⊥ O M$ hay $O C ⊥ M N (1)$

Ta có: $\hat{A N B} = \hat{A C B} = \frac{1}{2} \hat{A O B} = \frac{1}{2} {.90}^{0} = 45^{0}$ (góc nội tiếp và góc ở tâm cùng chắn cung AB)

Tam giác KBC có $\hat{B K C} = 90^{0}, \hat{K C B} = \hat{A C B} = 45^{0} \Rightarrow \hat{K B C} = 45^{0}$

$\Rightarrow \hat{A N B} = \hat{K B C} = 45^{0} .$ mà hai góc này ở vị trí so le trong $\Rightarrow B C / / A N$

Theo giả thiết ta có $B C ⊥ A I \Rightarrow A I ⊥ A N$ hay $M A ⊥ D N$ (từ vuông góc đến song song)

Mặt khác ta có : $B C ⊥ A I \Rightarrow A I ⊥ A N$

Xét tam giác DMN có hai đường cao $M A, N B$ cắt nhau tại H $\Rightarrow H$ là trực tâm của tam giác DMN

$\Rightarrow D H ⊥ M N (2)$

Từ (1) và (2) $\Rightarrow O C / / D H$ (đpcm)

Câu 13:

Cho phương trình $x^{2} - 2 m x - 2 m - 1 = 0 (1)$ với m là tham số. Tìm m để phương trình (1) có hai nghiệm phân biệt $x_{1}, x_{2}$ sao cho $\sqrt{x_{1} + x_{2}} + \sqrt{3 + x_{1} x_{2}} = 2 m + 1$

Xem đáp án

a) Ta có: $Δ' = m^{2} + 2 m + 1 = {(m + 1)}^{2}$

Để phương trình (1) có hai nghiệm phân biệt thì $Δ > 0 \Leftrightarrow {(m + 1)}^{2} > 0 \Leftrightarrow m \neq - 1$

Khi $m \neq - 1$ phương trình (1) có hai nghiệm phân biệt $\{\begin{cases} x_{1} = m + m + 1 = 2 m + 1 \\ x_{2} = m - (m + 1) = - 1 \end{cases}$

Theo bài ra ta có:

$\begin{array}{l} \sqrt{x_{1} + x_{2}} + \sqrt{3 + x_{1} x_{2}} = 2 m + 1 \Leftrightarrow \sqrt{2 m} + \sqrt{3 - (2 m + 1)} = 2 m + 1 \Leftrightarrow \sqrt{2 m} + \sqrt{2 - 2 m} = 2 m + 1 \\ \Leftrightarrow \{\begin{cases} 2 m + 1 \geq 0 \\ 2 m \geq 0 \\ 2 - 2 m \geq 0 \\ 2 m + 2 - 2 m + 2 \sqrt{2 m (2 - 2 m)} = 4 m^{2} + 4 m + 1 \end{cases} \Leftrightarrow \{\begin{cases} m \geq - \frac{1}{2} \\ m \geq 0 \\ m \leq 1 \\ 2 \sqrt{2 m (2 - 2 m)} = 4 m^{2} + 4 m - 1 \end{cases} \\ \Leftrightarrow \{\begin{cases} 0 \leq m \leq 1 \\ 4 (4 m - 4 m^{2}) = 16 m^{4} + 16 m^{2} + 1 + 32 m^{3} - 8 m^{2} - 8 m \end{cases} \Leftrightarrow \{\begin{cases} 0 \leq m \leq 1 \\ 16 m^{4} + 32 m^{3} + 24 m^{2} - 24 m + 1 = 0 \end{cases} \\ \Leftrightarrow \{\begin{cases} 0 \leq m \leq 1 \\ (2 m - 1) (8 m^{3} + 20 m^{2} + 22 m - 1) = 0 \end{cases} \Leftrightarrow \{\begin{cases} 0 \leq m \leq 1 \\ [\begin{array}{l} m = \frac{1}{2} \\ m \approx 0,044 \end{array} \end{cases} \Leftrightarrow [\begin{array}{l} m = \frac{1}{2} \\ m \approx 0,044 \end{array} (t m) \end{array}$

Vậy $m = \frac{1}{2}$ hoặc $m \approx 0,044$

Câu 14:

b,Cho hai số thực không âm a,b thỏa mãn $a^{2} + b^{2} = 2.$ Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức $M = \frac{a^{3} + b^{3} + 4}{a b + 1}$

Xem đáp án

Tìm giá trị lớn nhất

Ta có : $a b \geq 0 \Leftrightarrow a b + 1 \geq 1 \Leftrightarrow \frac{1}{a b + 1} \leq 1 \Leftrightarrow M = \frac{a^{3} + b^{3} + 4}{a b + 1} \leq a^{3} + b^{3} + 4$

Ta có: $\{\begin{cases} a, b \geq 0 \\ a^{2} + b^{2} = 2 \end{cases} \Leftrightarrow \{\begin{cases} a^{2} \leq 2 \\ b^{2} \leq 2 \end{cases} \Leftrightarrow \{\begin{cases} 0 \leq a^{3} \leq a^{2} \sqrt{2} \\ 0 \leq b^{3} \leq b^{2} \sqrt{2} \end{cases}$

Do đó: $a^{3} + b^{3} + 4 \leq a^{2} \sqrt{2} + b^{2} \sqrt{2} + 4 = \sqrt{2} . (a^{2} + b^{2}) + 4 = 2 \sqrt{2} + 4$

$\Rightarrow M \leq 2 \sqrt{2} + 4$

Dấu $" = "$ xảy ra $\Leftrightarrow [\begin{array}{l} a^{2} = 2 \\ b^{2} = 2 \\ a b = 0 \end{array} \Leftrightarrow [\begin{array}{l} \{\begin{cases} a = \sqrt{2} \\ b = 0 \end{cases} \\ \{\begin{cases} a = 0 \\ b = \sqrt{2} \end{cases} \end{array}$

Vậy $M a x M = 2 \sqrt{2} + 4 \Leftrightarrow [\begin{array}{l} \{\begin{cases} a = \sqrt{2} \\ b = 0 \end{cases} \\ \{\begin{cases} a = 0 \\ b = \sqrt{2} \end{cases} \end{array}$

Tìm giá trị nhỏ nhất

$\begin{array}{l} a^{3} + b^{3} + 1 \geq 3 \sqrt[3]{a^{3} . b^{3} .1} = 3 a b \\ \Rightarrow a^{3} + b^{3} + 4 \geq 3 a b + 3 = 3 (a b + 1) \\ \Leftrightarrow \frac{a^{3} + b^{3} + 4}{a b + 1} \geq 3 (d o .... a b + 1 > 0) \\ \Leftrightarrow M \geq 1 \end{array}$

Dấu "= " xảy ra

\Leftrightarrow \{\begin{cases} a = b \\ a^{2} + b^{2} = 2 \end{cases} \Leftrightarrow a = b = 1

Vậy $\min M = 3 \Leftrightarrow a = b = 1$

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 6

Danh sách câu hỏi

Bài thi liên quan