11 câu hỏi trắc nghiệm thuộc Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 9

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Đề số 1
Đề số 2
Đề số 3
Đề số 4
Đề số 5
Đề số 6
Đề số 7
Đề số 8
Đề số 9
Đề số 10
Đề số 11
Đề số 12
Đề số 13
Đề số 14
Đề số 15
Đề số 16
Đề số 17
Đề số 18
Đề số 19
Đề số 20
Đề số 21
Đề số 22
Đề số 23
Đề số 24
Đề số 25
Đề số 26
Đề số 27
Đề số 28
Đề số 29
Đề số 30

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 9

3340 lượt thi
11 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giải các phương trình, hệ phương trình sau: $x^{2} - 7 x + 10$

Xem đáp án

$x^{2} - 7 x + 10 = 0$ có $Δ = b^{2} - 4 a c = 7^{2} - 4.1.10 = 9 > 0$

Phương trình có 2 nghiệm phân biệt:

$[\begin{array}{l} x_{1} = \frac{7 + \sqrt{9}}{2.1} = 5 \\ x_{2} = \frac{7 - \sqrt{9}}{2.1} = 2 \end{array}$

Vậy phương trình có hai nghiệm phân biệt

x_{1} = 5; x_{2} = 2

Câu 2:

Giải các phương trình, hệ phương trình sau: $2) {(x^{2} + 2 x)}^{2} - 6 x^{2} - 12 x + 9 = 0$

Xem đáp án

$\begin{array}{l} 2) {(x^{2} + 2 x)}^{2} - 6 x^{2} - 12 x + 9 = 0 \\ \Leftrightarrow {(x^{2} + 2 x)}^{2} - 6 (x^{2} + 2 x) + 9 = 0 (*) \end{array}$

Đặt $x^{2} + 2 x = t .$ Khi đó ta có phương trình:

$\begin{array}{l} (*) \Leftrightarrow t^{2} - 6 t + 9 = 0 \Leftrightarrow {(t - 3)}^{2} = 0 \Leftrightarrow t - 3 = 0 \Leftrightarrow t = 3 \\ \Leftrightarrow x^{2} + 2 x = 3 \Leftrightarrow x^{2} + 2 x - 3 = 0 \Leftrightarrow x^{2} + 3 x - x - 3 = 0 \\ \Leftrightarrow x (x + 3) - (x + 3) = 0 \Leftrightarrow (x - 1) (x + 3) = 0 \\ \Leftrightarrow [\begin{array}{l} x + 3 = 0 \\ x - 1 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 3 \\ x = 1 \end{array} \end{array}$

Vậy phương trình đã cho có tập nghiệm $S = \{- 3; 1\}$

Câu 3:

Giải các phương trình, hệ phương trình sau:

$3) \{\begin{cases} 4 x - y = 7 \\ 5 x + y = 2 \end{cases}$

Xem đáp án

$3) \{\begin{cases} 4 x - y = 7 \\ 5 x + y = 2 \end{cases} \Leftrightarrow \{\begin{cases} 9 x = 9 \\ y = 4 x - 7 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 4.1 - 7 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = - 3 \end{cases}$

Vậy hệ phương trình có nghiệm duy nhất $(x; y) = (1; - 3)$

Câu 4:

Cho parabol (P): $y = \frac{1}{2} x^{2}$ và đường thẳng $(d) : y = x + m - 1$ (m là tham số)

a,Vẽ đồ thị (P)

Xem đáp án

Học sinh tự vẽ đồ thị (P)

Câu 5:

2, Gọi $A (x_{A}; y_{A}), B (x_{B}, y_{B})$ là hai giao điểm phân biệt của (d) và (P) Tìm tất cả các giá trị của tham số để m $x_{A} > 0$ và $x_{B} > 0$

Xem đáp án

2, Ta có phương trình hoành độ giao điểm của hai đồ thị hàm số (d) và (P)

$\frac{1}{2} x^{2} = x + m - 1 \Leftrightarrow x^{2} - 2 x - 2 m + 2 = 0 (*)$

Theo đề bài ta có: $(d)$ cắt (P) tại hai điểm $A (x_{A}, y_{A}), B (x_{B}, y_{B})$ phân biệt

$\Leftrightarrow (*)$ có hai nghiệm phân biệt $\Leftrightarrow Δ' > 0$

$\Leftrightarrow 1 - (- 2 m + 2) > 0 \Leftrightarrow 1 + 2 m - 2 > 0 \Leftrightarrow m > \frac{1}{2}$

Vậy với $m > \frac{1}{2}$ thì phương trình (*) có hai nghiệm $x_{A}, x_{B}$ phân biệt

Áp dụng hệ thức Vi-et ta có: $\{\begin{cases} x_{A} + x_{B} = 2 \\ x_{A} x_{B} = - 2 m + 2 \end{cases}$

Theo đề bài ta có: $\{\begin{cases} x_{A} > 0 \\ x_{B} > 0 \end{cases} \Rightarrow \{\begin{cases} x_{A} + x_{B} > 0 \\ x_{A} . x_{B} > 0 \end{cases} \Leftrightarrow \{\begin{cases} 2 > 0 \forall m \\ - 2 m + 2 > 0 \end{cases} \Leftrightarrow - 2 m > - 2 \Leftrightarrow m < 1$

Kết hợp các điều kiện của m ta được: $\frac{1}{2} < m < 1$

Vậy $\frac{1}{2} < m < 1$ thỏa mãn bài toán.

Câu 6:

Cho phương trình: $x^{2} + a x + b + 2 = 0$ (a,b là tham số)

Tìm các giá trị của tham số a,b để phương trình trên có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn điều kiện : $\{\begin{cases} x_{1} - x_{2} = 4 \\ x_{1}^{3} - x_{2}^{3} = 28 \end{cases}$

Xem đáp án

$x^{2} + a x + b + 2 = 0$ ta có: $Δ = a^{2} - 4 (b + 2) = a^{2} - 4 b - 8$

Để phương trình có 2 nghiệm phân biệt thì $Δ > 0 \Leftrightarrow a^{2} - 4 b - 8 > 0 (*)$

Khi đó, áp dụng định lý Viet ta có: $\{\begin{cases} x_{1} + x_{2} = - a \\ x_{1} x_{2} = b + 2 \end{cases}$

Theo bài ra ta có:

$\{\begin{cases} x_{1} - x_{2} = 4 \\ x_{1}^{3} - x_{2}^{3} = 28 \end{cases} \Leftrightarrow \{\begin{cases} x_{1} - x_{2} = 4 \\ {(x_{1} - x_{2})}^{3} - 3 x_{1} x_{2} (x_{1} - x_{2}) = 28 \end{cases} \Leftrightarrow \{\begin{cases} x_{1} - x_{2} = 4 \\ 4^{3} + 12 x_{1} x_{2} = 28 \end{cases} \Leftrightarrow \{\begin{cases} x_{1} - x_{2} = 4 \\ x_{1} x_{2} = - 3 \end{cases}$ mà

$x_{1} x_{2} = b + 2 \Rightarrow b + 2 = - 3 \Leftrightarrow b = - 3 - 2 = - 5$

Ta có: $\{\begin{cases} x_{1} + x_{2} = - a \\ x_{1} - x_{2} = 4 \end{cases} \Leftrightarrow \{\begin{cases} 2 x_{1} = 4 - a \\ 2 x_{2} = - a - 4 \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = \frac{4 - a}{2} \\ x_{2} = \frac{- a - 4}{2} \end{cases}$

$\begin{array}{l} \Rightarrow x_{1} x_{2} = - 3 \Leftrightarrow \frac{4 - a}{2} . (\frac{- a - 4}{2}) = - 3 \\ \Leftrightarrow (4 - a) (a + 4) = 12 \\ \Leftrightarrow 16 - a^{2} = 12 \Leftrightarrow a^{2} = 4 \Leftrightarrow [\begin{array}{l} a = 2 \\ a = - 2 \end{array} \end{array}$

Với $a^{2} = 4, b = - 5 \Rightarrow a^{2} - 4 b - 8 = 4 - 4. (- 5) - 8 = 16 > 0 \Rightarrow$ thỏa mãn điều kiện (*)

Vậy có 2 cặp số $(a, b)$ thỏa mãn yêu cầu bài toán là $(a, b) \in \{(2; - 5); (- 2; - 5)\}$

Câu 7:

Một tổ công nhân theo kế hoạch phải làm 140 sản phẩm trong một thời gian nhất định. Nhưng khi thực hiện năng suất của tổ đã vượt năng suất dự định là 4 sản phẩm mỗi ngày. Do đó tổng đã hoàn thành công việc sớm hơn dự định 4 ngày. Hỏi thực tế mỗi ngày tổ đã làm được bao nhiêu sản phẩm.

Xem đáp án

Gọi số sản phẩm thực tế mỗi ngày tổ công nhân sản xuất được là x (sản phẩm) $(x \in ℕ *, x > 4)$

$\to$ Thời gian thực tế mà tổ công nhân hoàn thành xong 140 sản phẩm là $\frac{140}{x}$ ngày

Theo kế hoạch mỗi ngày tổ công nhân đó sản xuất được số sản phẩm: x-4

$\to$ Thời gian theo kế hoạch mà tổ công nhân hoàn thành xong 140 sản phẩm: $\frac{140}{x - 4}$ (ngày)

Theo đề bài ta có thời gian thực tế hoàn thành xong sớm hơn so với thời gian dự định là 4 ngày nên ta có phương trình:

$\begin{array}{l} \frac{140}{x - 4} - \frac{140}{x} = 4 \\ \Rightarrow 140 x - 140 (x - 4) = 4 x (x - 4) \\ \Leftrightarrow 35 x - 35 (x - 4) = x (x - 4) \\ \Leftrightarrow x^{2} - 4 x - 140 = 0 \\ \Leftrightarrow x^{2} - 14 x + 10 x - 140 = 0 \\ \Leftrightarrow x (x - 14) + 10 (x - 14) = 0 \\ \Leftrightarrow (x + 10) (x - 14) = 0 \\ \Leftrightarrow [\begin{array}{l} x + 10 = 0 \\ x - 14 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = - 10 (k t m) \\ x = 14 (t m) \end{array} \end{array}$

Vậy thực tế mỗi ngày tổ công nhân đã làm được 14 sản phẩm .

Câu 8:

Cho đường tròn (O, R).Từ một điểm M ở ngoài đường tròn ( O,R) sao cho OM= 2R vẽ hai tiếp tuyến $M A, M B$ với $(O) (A, B$ là hai tiếp điểm). Lấy một điểm N tùy ý trên cung nhỏ AB Gọi I,H,K lần lượt là hình chiếu vuông góc của N trên $A B, A M, B M .$

a, Tính diện tích tứ giác MAOB theo R

Xem đáp án

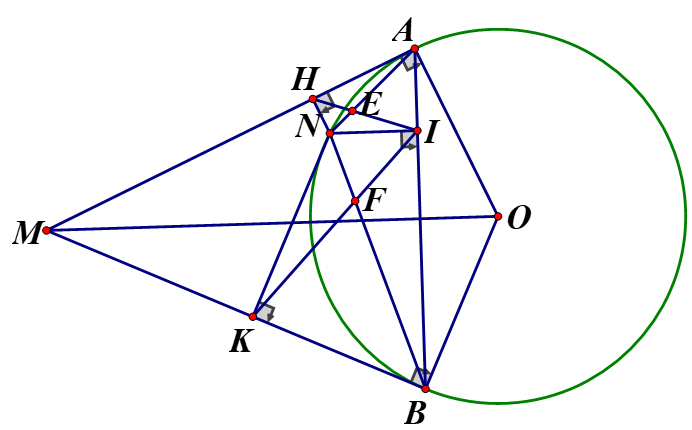
Cho đường tròn (O, R).Từ một điểm M ở ngoài đường tròn ( O,R) sao cho OM=2R (ảnh 1)

Xét $Δ O A M$ và $Δ O B M$ ta có:

$O A = O B (= R);$ OM chung; $M A = M B$ (tính chất hai tiếp tuyến cắt nhau)

$\Rightarrow Δ O A M = Δ O B M (c . c . c) \Rightarrow S_{O A M} = S_{O B M} \Rightarrow S_{M A O B} = S_{O A M} + S_{O B M} = 2 S_{O A M}$

Áp dụng định lý Pytago trong tam giác vuông OAM ta có:

$\begin{array}{l} A M^{2} = O M^{2} - O A^{2} = {(2 R)}^{2} - R^{2} = 3 R^{2} \Rightarrow A M = R \sqrt{3} \\ \Rightarrow S_{M A O B} = 2 S_{O A M} = 2. \frac{1}{2} O A . A M = R . R \sqrt{3} = R^{2} \sqrt{3} (d v d t) \end{array}$

Câu 9:

2) Chứng minh:

\hat{N I H} = \hat{N B A}

Xem đáp án

2,Xét tứ giác AINH có $\hat{A I N} + \hat{A H N} = 90^{0} + 90^{0} = 180^{0} \Rightarrow A I N H$ là tứ giác nội tiếp

$\Rightarrow \hat{N I H} = \hat{N A H}$ (hai góc nội tiếp cùng chắn cung HN)

Mà $\hat{N A H} = \hat{N B A}$ (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn $\overset{⏜}{A N})$

$\Rightarrow \hat{N I H} = \hat{N B A} (= \hat{N A H}) (d f c m)$

Câu 10:

3, Gọi E là giao điểm của AN và IH, F là giao điểm của BN và IK. Chứng minh tứ giác IENF nội tiếp được trong đường tròn.

Xem đáp án

3,Xét tứ giác NIBK ta có: $\hat{N I B} + \hat{N K B} = 90^{0} + 90^{0} = 180^{0}$ mà hai góc này là hai góc đối diện $\Rightarrow N I B K$ là tứ giác nội tiếp $\Rightarrow \hat{K B N} = \hat{N I K}$ (2 góc nội tiếp cùng chắn $\overset{⏜}{K B})$

Xét đường tròn (O) ta có: $\hat{K B N} = \hat{N A B}$ ( góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn $\overset{⏜}{B N})$ $\Rightarrow \hat{N I K} = \hat{N A B} (= \hat{K B N})$

Xét $Δ A N B$ có: $\hat{A N B} + \hat{N A B} + \hat{N B A} = 180^{0}$ (tổng 3 góc trong một tam giác)

Lại có: $\hat{N I H} = \hat{N A B} (c m 2) = \hat{N I E}; \hat{N I K} = \hat{N A B} (c m t) = \hat{N I F}; \hat{A N B} = \hat{E N F}$

$\Rightarrow \hat{E N F} + \hat{E N I} + \hat{N I F} = \hat{E N F} + \hat{E I F} = 180^{0}$

Mà $\hat{E N F,} \hat{E I F}$ là hai góc đối diện $\Rightarrow$ Tứ giác NEIF là tứ giác nội tiếp

Câu 11:

4, Giả sử O, N, M thẳng hàng. Chứng minh $N A^{2} + N B^{2} = 2 R^{2}$

Xem đáp án

Theo đề bài ta có O, N, M thẳng hàng $\Rightarrow O N = R = \frac{1}{2} O M \Rightarrow N$ là trung điểm của OM

Ta có: $O N ⊥ A B = \{I\} \Rightarrow I$ là trung điểm của AB (tính chất đường kính dây cung)

Lại có: $O A = O B = R \Rightarrow O N$ là đường trung trực của $A B \Rightarrow N A = N B$

Xét $Δ M A O$ ta có: $\cos \hat{A O M} = \frac{O A}{O M} = \frac{R}{2 R} = \frac{1}{2} \Rightarrow \hat{A O M} = 60^{0} = \hat{A O N}$

Xét $Δ A O N$ ta có: $\{\begin{cases} O A = O N = R \\ \hat{A O N} = 60^{0} \end{cases} \Rightarrow Δ A O N$ là tam giác đều.

\begin{array}{l} \Rightarrow N A = O N = O A = R = A B \\ \Rightarrow N A^{2} + N B^{2} = R^{2} + R^{2} = 2 R^{2} (d f c m) \end{array}

Bắt đầu thi ngay

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 9

Danh sách câu hỏi

Bài thi liên quan