Thứ năm, 20/02/2025
Đăng ký Đăng nhập
IMG-LOGO
Trang chủ Lớp 9 Toán Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)

Tổng hợp đề thi chính thức vào 10 môn Toán năm 2019 có đáp án (Phần 1)- Đề 13

  • 5217 lượt thi

  • 10 câu hỏi

  • 45 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

a, Thực hiện phép tính: 49−325
Xem đáp án

a, 49−325=4.3−3.5=12−15=−3

Câu 2:

b, Cho hàm số y=ax2a≠0.Tìm giá tri của a để x= 2 thì y=-8 
Xem đáp án

b, Thay x=2,y=−8 vào công thức y=ax2a≠0ta được:

−8=22.a⇔4a=−8⇔a=−2(tm)

Vậy a=−2

Câu 3:

c, Giải phương trình 3x2−5x+2=0
Xem đáp án

c, 3x2−5x+2=0, phương trình có dạng a+b+c=3−5+2=0  nên có hai nghiệm phân biệtx1=1x2=23

Vậy S=1;23

Câu 4:

d, Giải hệ phương trình: 3x−1y=95x+1y=7
Xem đáp án

Điều kiện x≠0,y≠0 , Đặt 1x=a1y=ba,b≠0.Khi đó ta có hệ phương trình:

⇔3a−b=95a+b=7⇔8a=16b=3a−9⇔a=2b=−3(tm)⇒1x=21y=−3⇔x=12(tm)y=−13(tm)

Vậy hệ phương trình có nghiệm x,y=12,−13

Câu 5:

Thầy Minh đi xe máy từ địa điểm A đến địa điểm B cách nhau 60km với vận tốc không đổi. Khi từ B trở về A do trời mưa, thầy Minh giảm vận tốc của xe máy xuống 10km/h so với lúc đi nên thời gian lúc về nhiều hơn thời gian lúc đi 30 phút. Hỏi lúc về thầy Minh đi xe máy với vận tốc bao nhiêu ?
Xem đáp án

Gọi vận tốc lúc về của thầy Minh là x(km/h)(x>0)

⇒Thời gian về của thầy Minh là : 60x(giờ)

Do lúc về thầy Minh giảm tốc độ xuống 10km/h so với lúc đi nên vận tốc lúc đi của thầy Minh là: x+10(km/h) ⇒Thời gian lúc đi của thầy Minh: 60x+10(h) 

Theo đề bài ta có thời gian lúc về nhiều hơn thời gian lúc đi 30 phút =12giờ nên ta có phương trình:

60x−60x+10=12⇒120(x+10)−120x=x(x+10)⇔x2+10x−1200=0⇔x2+40x−30x−1200=0⇔xx+40−30(x+40)=0⇔x+40x−30=0⇔x+40=0x−30=0⇔x=−40(ktm)x=30(tm)

 

Vậy vận tốc lúc về của thầy Minh là 30km/h

Câu 6:

Cho ∆ABC vuông tại A với BC=13cm,AB=5cm.

a, Tính độ dài cạnh AC 
Xem đáp án
Cho tam giác ABC vuông tại A với  BC= 13cm, AB = 5cm a) Tính độ dài cạnh AC  (ảnh 1)

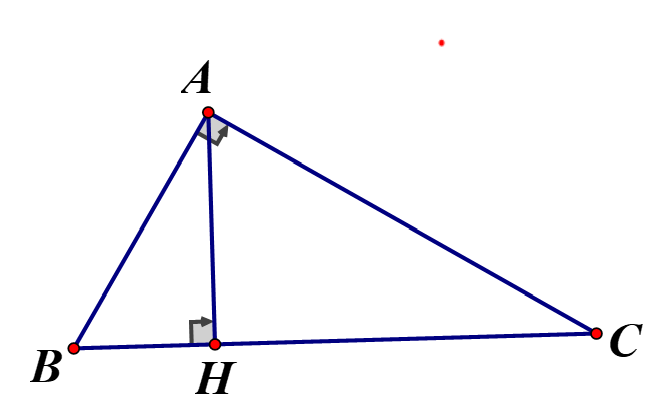
Áp dụng định lý Pytago cho ΔABC vuông tại A ta có:

AC2=BC2−AB2=132−52=144⇒AC=12cm

Câu 7:

b, Kẻ đường cao AH Tính độ dài đoạn thẳng AH 
Xem đáp án

     Áp dụng hệ thức lượng cho ΔABC vuông tại A và có đường cao AH ta có:

AH.BC=AB.AC⇔AH=AB.ACBC=5.1213=6013(cm)

Câu 8:

Từ điểm A nằm ngoài đường tròn (O) kẻ lần lượt hai tiếp tuyến AB, AC với đường tròn (O) (B, C là hai tiếp điểm). Trên cung nhỏ BC lấy một điểm P bất kỳ (P khác B và C), từ P kẻ các đường thẳng PQ,PE,PF lần lượt vuông góc với các cạnh BC,AC,AB Q∈BC,E∈AC,F∈AB

a, Chứng minh tứ giác PECQ nội tiếp
Xem đáp án
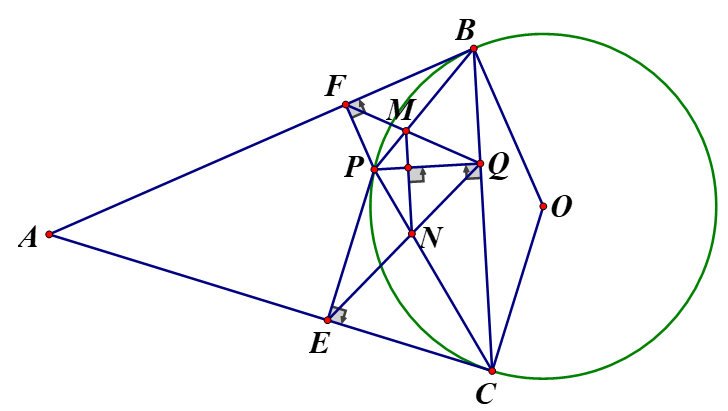
Từ điểm A nằm ngoài đường tròn (O) kẻ lần lượt hai tiếp tuyến AB, AC với đường tròn (O) (B, C là hai tiếp điểm). (ảnh 1)

a, Xét tứ giác PECQ ta có: PQC^=900PQ⊥BCPEC^=900PE⊥AC⇒PQC^+PEC^=900+900=1800

Mà hai góc này ở vị trí đối diện nên PECQ là tứ giác nội tiếp

Câu 9:

b, Gọi M là giao điểm của PQ và FQ, N là giao điểm của PC và EQ. Chứng minh rằng MN⊥PQ
Xem đáp án

Ta có tứ giác PECQ nội tiếp (cmt)⇒PQE^=PCE^(cùng chắn cung PE)

Lại có: PCE^=PBC^ (góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn PC)

⇒PQE^=PBC^ hay PBC^=PQN^=PCE^(1)

Xét tứ giác PFBQ ta có: PQB^=900PQ⊥BCPFC^=900PF⊥AB⇒PQB^+PFC^=900+900=1800

Mà hai góc này ở vị trí đối diện⇒PFBQlà tứ giác nôi tiếp

⇒FBP^=FQP^ (cùng nhìn PF)

Lại có: PBF^=BCP^(góc nội tiếp và góc tạo bởi tiếp tuyến dây cung cùng chắn PB⏜)

⇒PQF^=PCB^ hay PCB^=PQM^=PBF^(2)

Xét ΔPBC có: BPC^+PBC^+PCB^=1800(tổng 3 góc trong tam giác ) (3)

Từ (1) (2) (3)

⇒BPC^+MQP^+PQN^=MPN^+MQP^+PQN^=MPN^+MQN^=1800

⇒MPNQ là tứ giác nôi tiếp ⇒PMN^=PQN^(hai góc nội tiếp cùng chắn cung PN)

⇒PMN^=PBC^=PQN^, mà hai góc này ở vị trí đồng vị ⇒MN//BC

Lại có BC⊥PQ⇒MN⊥PQ(dfcm)

Câu 10:

Cho biểu thức P=mx−2019x2(x≠0). Tìm các số thực dương m để biểu thức P có giá trị lớn nhất bằng 2019
Xem đáp án

Ta có:

P=mx−2019x2=mx−2019x2=−2019.1x2−m2019x=−20191x−m40382+m28076≤m28076

Mà theo đề MaxP=2019⇔m28076=2019⇔m=4038

Bắt đầu thi ngay

Bài thi liên quan